Сила Кориолиса и центробежная сила в электродинамике и механике

Существующее представление о природе силы Кориолиса и центробежной силы вызывают много недоуменных вопросов. В статье доказывается, что эти силы могут быть обоснованы как следствие уравнений Максвелла для гравитомагнетизма.

Оглавление

• 1.    Вступление \ 67

• 2.    Взаимодействие движущихся электрических зарядов \ 69

• 3.    Взаимодействие вращающегося электрического заряда с неподвижным полем электрических зарядов \ 69

• 4.    Уравнения Максвелла для гравитомагнетизма и сила

• 5.    Центробежная сила \ 72

Кориолиса\ 71

Литература \ 73

1.    Вступление

Современные представления о силе Кориолиса [1] заключаются в следующем:

• •    сила Кориолиса никак не связана с каким-либо взаимодействием рассматриваемого тела с другими телами,

• •    сила Кориолиса обусловлена выбором конкретной неинерциальной системы отсчёта.

• •    сила Кориолиса не является физической силой и не совершает работу.

Грубо говоря, сила Кориолиса, действующая на тело, появляется потому, что рядом с этим телом вращается с определенной скоростью другое тело. Наше тело не взаимодействует с этим телом и потому «не знает» величину этой скорости, но именно от этой скорости зависит сила Кориолиса. Масса этого другого тела и расстояние до него не имеют значения. Сила Кориолиса не совершает работу, но

• •    свободно падающее тело отклоняется,

• •    рельсы железных дорог с односторонним движением снашиваются неравномерно,

• •    снаряды дальнобойной артиллерии отклоняются от расчетной траектории и т.п.

Итак,

• •    имеется инерциальная система отсчета, вращающаяся с вектором угловой скорости <У,

• •    имеется неинерциальная система отсчета, никак не взаимодействующая с неинерциальной системой отсчета,

• •    в неинерциальной системе тело массой т движется со скоростью V,

• •    при этом наблюдается сила Кориолиса, действующая на тело перпендикулярно скорости V, которую определяют по формуле

2.    Взаимодействие движущихся электрических зарядов

F_K = —2т(<у х V) .                                 (0)

Эта сила наблюдается, как фиктивная, из неинерциальной системы отсчета, как, например, в опыте с маятником Фуко. Но эта же сила наблюдается также из инерциальной системы отсчета, как, например, реальная сила подмыва берегов. Наблюдение может вестись еще из третьей системы , в которой вращается неинерциальная система отсчета, в которой находится инерциальная система отсчета, как в опыте [5]. В этом случае мы наблюдаем, как в неинерциальной системе фиктивная сила физически рисует спираль… Поэтому силу Кориолиса нельзя считать фиктивной и объяснять особенностями восприятия наблюдателя.

Необходимо пытаться найти физическую связь реальной вращающейся системы с телом, движущейся в ней или около этой системы.

Далее показывается, что сила Кориолиса обнаруживается как следствие уравнений Максвелла для гравитомагнетизма. Эти уравнения существуют в окрестности гравитирующего тела (Земли). Следовательно, сила Кориолиса может возникнуть только в окрестности такого тела и не может быть в открытом Космосе. Сила Кориолиса – полноценная сила, совершающая работу. Энергия, затрачиваемая на выполнение этой работы, доставляется гравитирующим телом.

Рис. 1.

Рассмотрим рис. 2, где в точках А и В показаны два заряда q₁ и q₂ , движущиеся со скоростями V₁ и V₂ соответственно. Известно, что магнитная индукция поля, создаваемого зарядом q₂ в точке, где в данный момент находится заряд q₁ , равна

5 = q2(V?xr)/r3.

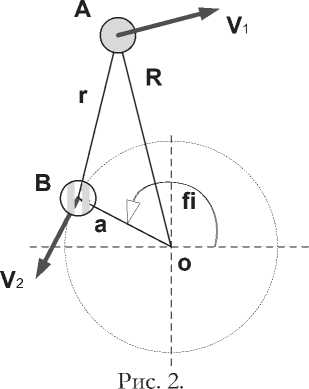
При этом вектор r направлен из точки, где находится движущийся заряд q1. Сила Лоренца, действующая на заряд q1, ^12 = qi(v^x в).(2)

или

^12 = q^V. x(V2x r))^3)-

На рис. 2 показаны также векторы а и R, причем вектор а составляет с горизонтальной осью ох угол ф и г = R — a.(4)

Вначале мы рассмотрим случай, когда все эти векторы лежат в горизонтальной плоскости оу, и будем обозначать проекции всех векторов нижним индексом координаты. Тогда вектор

W = (V2 X F) = z(v2xry — V2yTx),(5)

где z — орт вертикальной оси. Обозначим wz = (v2xry — V2yrxy(6)

Тогда

W = zwz.(7)

Если заряд ^2 вращается вокруг точки О с угловой скоростью to, то вектор

v ₂ = toaexp

Of)

является касательным к окружности с радиусом а. При этом

^w z

= toa

(_Со5 (^+ 2 ^)r y

- sin (^ + ^ ^r x ⁾

или wz = —toa(sin(^)ry + соз(ф)Fx)-

Из (3, 5) получим:

F12 = 9192(V1 X w)/(r3)

или, с учетом (7, 10),

F12 = 4i42to (V7 X z~)/(r3).

Предположим теперь, что величина 92 является плотностью зарядов, расположенных равномерно на всей горизонтальной плоскости, а эта плоскость вращается с угловой скоростью to вокруг точки О. При этом линейная скорость V2 каждой точки определяется по (8).

Найдем силу, действующую от такой заряженной и вращающейся плоскости на заряд 9₁:

	F = J F12dфda = J (q7q2to (v7 X 7^)/(г3У) йфйа ф,а                ф,а
или	F = 9 1 9 2 (^ 7 XtoW) ,                             (13)
где	й) = Zto ,                                                   (14) W = ^ ФД " т- з d^da-                               (15)

Из (15, 10) находим:

W = - f ” ^а(fo ^ Csin(^)r y + cos(^)r_x)r ³ ^^) da, (16) где r определяется по (4):

rx = Rx — acos(^), ry = Ry — asin(^), ax = acos(^), ay = asin(^).

Интегрирование по этим формулам дает замечательный результат: величина W не зависит от R и при стремлении верхнего предела к го приближается к величине

W « —45.

Поэтому формулу (13) можно записать в виде

F = q^W^ х с),(20)

Можно заметить аналогию между формулами для силы (20) и для силы Кориолиса.

3.    Взаимодействие вращающегося электрического заряда с неподвижным полем электрических зарядов

Рассмотрим теперь электрический заряд q^ который вращается над полем электрических зарядов. Силы Кулона со стороны вращающегося заряда должны вращать поле электрических зарядов. При этом задача сводится к предыдущей: действительно, заряд q₁ движется над вращающимся полем электрических зарядов. Для идентичности этих задач надо еще предположить, что поле зарядов не имеет собственного вращения или скорость этого вращения существенно меньше скорости вращения заряда q p Таким образом, и в этом случае мы можем воспользоваться формулой (20). Линейная скорость Г₁ заряда q₁ и его угловая скорость с связаны формулой

V₁ = Rc ,                                    (20a)

где R - радиус вращения заряда q₁ . Совмещая (20, 20a ) находим:

F = q₁q₂WRc² .                           (20b)

Можно заметить аналогию между формулами для силы ( 20b ) и для центробежной силы.

4.    Уравнения Максвелла для гравитомагнетизма и сила Кориолиса

В [2] автор предлагает новое решение уравнений Максвелла для гравитомагнетизма, которое используется для построения математических моделей различных природных явлений (песчаного вихря, морских течений, водоворота, воронки, водного солитона, водного и песчаного цунами, турбулентных течений, дополнительных (неньютоновских) сил взаимодействия небесных тел). Во всех этих моделях используется представление о массовых токах, как о потоках частиц масс. Скорость массовых частиц может быть очень мала и часто их поток может быть невидим также, как поток электронов. Но существование указанных явлений и возможность построения указанных математических моделей, аналогичных математическим моделям постоянного тока в электродинамике [4], подтверждают предположение о существовании массовых токов и взаимодействии массовых частиц, полностью аналогичном взаимодействию электрических зарядов.

На основе этого можно предположить, что вращение тела сопровождается массовым током, аналогично тому, как вращение заряженного тела сопровождается конвекционным электрическим током. Эйхенвальд [3] показал, что такой ток создает магнитную индукции. Исходя из полной аналогии между уравнениями Максвелла для электродинамики и гравитомагнетизма [2] можно утверждать, что при вращении тела создается гравитомагнитная индукция. На массу т , движущуюся в гравимагнитном поле со скоростью V , действует гравитомагнитная сила Лоренца (аналог магнитной силы Лоренца).

Исходя из вышесказанного перепишем формулу (20), полученную выше для взаимодействия электрических зарядов, в применении к взаимодействию массовых зарядов:

F = Wpm(V х щ) ,                            (21)

где W « -45, т, V - масса и скорость движущегося тела, р - поверхностная плотность масс, как элементов массового тока,

<ц - угловая скорость вращения плоскости, на которой равномерно распределены эти элементы.

Сравнивая формулы (0, 21) находим, что

-2 = Wp,(22)

откуда следует, что плотность масс р = --« 0.044-^ = 4.4 •lO-5-^.

г W         т2             sm24

«Позвольте»,  - удивится внимательный читатель.  «Вы отвергаете теорию Кориолиса и одновременно с этим пользуетесь его формулой?» Я могу только присоединиться к его удивлению и еще более удивиться тому, что столь разные методы рассуждений привели к одному и тому же формульному результату! Все же вывод плотности масс (23) можно принять только в том случае, если есть уверенная экспериментальная проверка величины коэффициента «2» в формуле (0) силы Кориолиса.

Используемый метод вывода силы Кориолиса доказывает реальность, а не фиктивность этой силы и обнаруживает источник мощности для этой силы – гравитационное поле Земли.

5.    Центробежная сила

Как показано в разделе 3, вращение заряженной плоскости под движущимся зарядом можно заменить вращением заряда над заряженной плоскостью. Тогда в формуле (20) <У — это вектор угловой скорости вращающегося заряда, линейная скорость этого заряда

VT = Rto.(24)

В применении формулы ( 20b ) к взаимодействию массовых зарядов получаем:

F = Wpm(2R.(25)

Эта формула отличается от формулы для центробежной силы

Fc = m(2R, только коэффициентом. По аналогии с предыдущим здесь находим плотность масс p = - - « 0.022 ^ = 2.2 • 10"5

r W         m2              sm2k

Таким образом, природа центробежной силы такая же, как и природа силы Кориолиса, а источник мощности для этой силы – гравитационное поле Земли.