Сильно нелинейная теория упругих и неупругих деформаций кристаллических тел

VV

Производные по времени обозначены точками сверху, а пространственные производные - запятой в тензорных индексах. Далее введены обозначения для тензорных материальных коэффициентов: макроупругости (X ikmn ), микроупругости ( k_ikmn ), стрикции ( S ik ), половины межатомного потенциального барьера или энергии активации межатомных связей( р ). Величина Ф ( u_R ) представляет собой периодическую энергию взаимодействия подрешеток, которая будет проанализирована подробно.

Отметим, что все материальные тензоры имеют четный ранг. Это значит, что мы рассматриваем кристаллы, обладающие центром симметрии, для которых тензоры нечетных рангов обращаются в нуль. Этот последний случай рассмотрен в работах [4,5].

Общие вариационные уравнения для полей макро- и микросмещений имеют вид

POi=^«mnU.m„ - Sin [Ф(Ur )]n;(1.4)

PU = kikmnuk,mn -(P - SIU»,. )5Ф/5ui .(1.5)

Первое уравнение полезно переписать в стандартной форме уравнения механики сплошной среды

P Ui=sik, k,(1-6)

введя определение тензора напряжений ik ikmn m,n      ik R ..

Соотношения (1.5)–(1.7) представляют трансляционно-инвариантные уравнения динамики двойного континуума. Прежде чем заняться их анализом, уточним вид периодической энергии взаимодействия подрешеток Ф .

В общем случае энергия Ф является функцией трех проекций ( и 1 = u • k , и 2 = u • m , и 3 = u • n ) вектора u на орты кристаллографических осей ( k,m,n ). Они инвариантны к точечным преобразованиям общей системы координат. Тогда для вектора силы взаимодействия пары атомов

F = 5Ф/5u = (5Ф(5и 1 )k + (5Ф/5и2 )m + (5Ф/5и3 )n .               (1.8)

В этом общем случае речь должна идти о трояко периодической функции Ф ( u_R ) при взаимной трансляции подрешеток Бравэ вдоль направлений векторов k,m,n на периоды a 1 , a ₂ , a 3 соответственно. Основная идея состоит в том, чтобы построить скалярную периодическую функцию от простейших поворотных инвариантов u_R векторного поля, выбранных, в частности, в виде

^UR = V ^{U а} k uk .                                    (1-9)

Построение конкретной теории требует введения функции Ф в явной форме. Простейшим случаем будет

^Ф^ p ^[ 1 - cos ^и, ^а .^ик J ^а ik = a - 2 ^ki^ki ⁺ a - m i m i ⁺ a 3 - 2 n i n i •          (i.i°)

Здесь a _ik - тензор обратных периодов решетки ( a 1 , a ₂ , a ₃ ), а k/ a 1 , m/ a ₂ , n/ a ₃ -векторы обратной решетки. Очевидно, k a ₁, m a ₂ , n a ₃ есть векторы решетки Бравэ. Сила взаимодействия соседних атомов

5Ф 5Ф 5ur     5ид .            ,-------

Fi = — = — — =- — sin ^uR , ^uR = ^ ^ui « ik^uk •           (1.11)

5 u i   5 u_R д u i      5 u i

Для кристаллов кубической симметрии (a1 = a2 = a3 = a) получим более простые соотношения a ik = a-2 (kiki + mim, + nini), uR = ui a ku.i = и2 a-2,                (1.12)

Fi =- pL i sin u_R ; u R = ( u X + u 2 + u ²)/ a , L i = uju , u = J u x + u^ + u 2 •    (1-13)

Очевидно u – абсолютная величина вектора микросмещений, L_i – его орт.

Легко видеть, что обе функции периодичны вдоль направлений k,m,n с периодами a 1 , a ₂ , a 3 соответственно. Поскольку смещение u исчисляется в единицах относительно периода решетки Бравэ (в данном направлении), то периодами этой функции являются целые числа. В частности, если F ^ p sin( u ), то смещению u = |u| = 2 п отвечает переход подрешеток в новое, но кристаллографически эквивалентное (ближайшее) структурное состояние. Но при таком переходе происходит переключение связей и изменение ближайших соседей каждого атома, т.е. изменение локальной топологии.

Перепишем общие уравнения для случая, когда периодическая функция Ф выбрана согласно (1.10) и учитываются соотношения (1.12). Получим

^» =\ kmn U m , n - S k (1 - cos u r ),                      (1.14)

I                     ^duR •                      / 2                                          1

Ц u i = k kmn u k , mn ^- P — sin u R , u R = V u i O k u k •               ^(М5)

d u i

Первое соотношение позволяет рассматривать напряжение как сумму упругой части (первое слагаемое) и неупругой, обусловленной перестройкой микроструктуры решетки. Последняя исчезает при нулевых микросмещениях и достигает предельно высокого значения, равного S_ik , когда u = п , т.е. при сдвиге всех атомов из потенциальных ям в максимумы – на вершины межатомных потенциальных барьеров. Очевидно, величина материального тензора S_ik является тем максимальным (теоретическим) пределом для неупругих напряжений, который отвечает потере устойчивости решетки – в условиях однородных полей. Более интересны неоднородные пластические деформации, фазовые переходы и другие бифуркационные процессы. Они определяются полем микросмещений, которое является решением уравнения (1.15). В этом случае проблема устойчивости требует серьезного анализа, который будет развит далее.

(2.1)

1 H X 2 k 2

D =      -( U J + -( u J²

H Jo 2     ’ ^x 2 ’ x

-

( p - SU , _x )(1 - cos u ) dx .

(2.2)

Кроме того, U_x и u _x - макро- и микроскопические градиенты; X, k - макро-, микроскопические модули; S – коэффициент нелинейной стрикции; 2 p – межатомный потенциальный барьер в недеформированной решетке (энергия активации атомных связей в элементарной ячейке).

Соответствующие уравнения равновесия имеют вид

0 = XU,„ - 5(1 - cos u)xx(2.3)

0 = ku,xx -(p - SU,x)sin u .

Первый интеграл первого уравнения имеет вид

X Ux - S cos u = о- const.(2.5)

Здесь σ представляет собой фактически напряжение в теле, обусловленное как макроскопическими деформациями, так и микросмещениями. Исключая с его помощью макроградиентный член во втором уравнении, получим отдельное уравнение для мик- роскопического поля,

0 = ku xx + (S2/x)sinu(1 - cosu) - (p - Sо X)sin u .(2.6)

Оно также один раз интегрируется. Его первый интеграл

(k/2)u^ = (S2/2x)sin2 u + (p - Sо/X - S2/X)(1 - cosu) + G.(2.7)

Вторая константа интегрирования G также имеет простой смысл. Так если на границе равны нулю микросмещения ( u_s = 0), то

G = (k / 2)( u 2) s; us = 0.(2.8)

Если же на границе равны нулю градиенты, то константа G позволяет выбрать граничное значение микросмещения u_s с помощью соотношения

(s 2/2x)sin2 us + (p - S о/X-S2 /X)(1 - cos us) = - G, (k/ 2)(u 2x)s = 0.(2.9)

Таким образом, с помощью G задаются граничные условия для уравнения микрополя (2.6). В общем виде можно учесть произвольные граничные условия

u (0) = u_s , ( kJ 2 ) ( u²_x ) s - ( S ²/2 X ) sin ² u_s - ( p - S о/X- S ²/X )(1 - cos u_s ) = G .     (2.10)

Далее будет показано, что уравнение (2.7) интегрируется в общем, виде с учетом произвольных граничных условий. Более того, в общем виде может быть вычислена и полная энергия D . Действительно, исключим вначале из выражения (2.2) градиентные слагаемые с помощью выражений (2.5) и (2.7) для первых интегралов. Получим выражение

D = - L j ₀ H [ ( о ²/2 x ) + G + (2 p - о S /X )(1 - cos u ) - ( S² /x) (1 - cos u ) ² ] dx . (2.11)

Здесь первое слагаемое (константа) представляет плотность макроскопической упругой энергии, а второе (константа интегрирования G ) связано с плотностью энергии микроградиентов на границе. Обе константы дают вклад в энергию пропорционально размеру тела.

Интересно третье слагаемое под знаком интеграла. Сравнивая его с последним слагаемым в (2.2), видно, что энергия жесткого сдвига подрешеток изменилась в деформируемом состоянии за счет снижения потенциального межатомного барьера (2 p ) в элементарной ячейке на величину, пропорциональную напряжениям σ, и, конечно, коэффициенту стрикции S . Роль стрикции (взаимодействия макро- и микродеформации) этим не ограничивается. Последнее слагаемое определяет дополнительное снижение упругой энергии за счет изменения самой структуры независимо от напряжений.

Существенно, что выражение для полной энергии может быть проинтегрировано в общем виде при произвольных граничных условиях. Перейдем для этого к интегрированию по микроскопическому полю (от интегрирования по пространству) в результате замены dx = du I u _x = du I R ( u ), где R ( u ) находится из (2.7) и будет раскрыто чуть ниже. Используя выражение для первого интеграла (2.7), запишем

DH - H о 2/ 2 Х = ( 2/ k ) 1/² u S [ g + (2 p - о S /Х)(1 - cos u ) - ( S ²/х ) (1 - cos u ) ² R ( u ) dx . (2.12) 0

Здесь

R ( u ) = [ ( S ²/2 x ) sin ² u + ( p - S g/X- S ²/X )(1 - cos u ) + G ] ^{- 1}/² . (2.13)

Существенно, что этот интеграл выражается в общем виде, правда, через эллиптические функции. Он представляет микроскопическую энергию изменения структуры тела при деформировании в зависимости лишь от граничных значений микроскопического поля u_s и его градиентов и, разумеется, от материальных констант λ, p , S . Для его вычисления не требуется знания решения уравнения микрополя (2.7).

На рис.2 показана зависимость интеграла от граничного значения поля u_s при некоторых значениях констант G , p , S , λ. Видно, что это кривые с локальными минимумами и потенциальными барьерами.

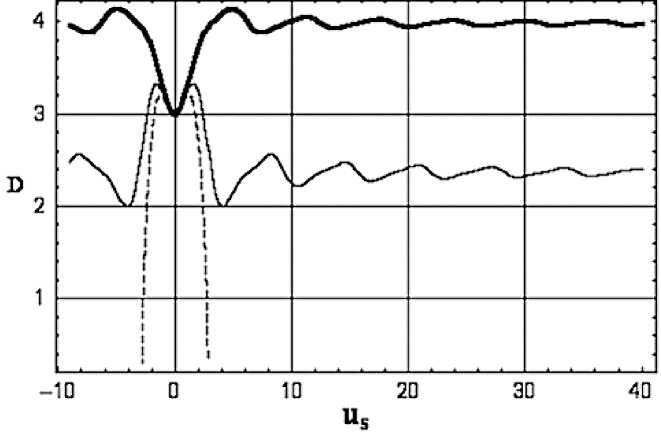
Рис.2. Зависимость плотности энергии деформации от микросмещения на границах при различных напряжениях.

Нижняя пунктирная кривая описывает разрушение.

Средняя отвечает фазовому (структурному) переходу в метастабильное состояние. Верхняя кривая отвечает случаю деградации свойств материала по мере накопления структурных изменений, когда потенциальные барьеры становятся все ниже

Нижняя пунктирная кривая описывает разрушение, средняя – отвечает фазовому (структурному) переходу в метастабильное состояние, которое может эволюционировать в сторону нарастания структурных изменений, когда изменение внутренней структуры нарастает. И, наконец, верхняя кривая отвечает случаю деградации свойств мате-

Сильно нелинейная теория упругих и неупругих деформаций кристаллических тел риала по мере накопления структурных изменений, когда потенциальные барьеры становятся все ниже.

Они исчезают, если относительный потенциальный барьер становится критически малым. Это значит, что структура решетки становится нестабильной. Этот эффект влияния изменений структуры на прочность решетки будет обсуждаться дополнительно.

Общее решение уравнения микрополя

Энергетическая устойчивость решетки в одномерном случае рассмотрена выше без обращения к явному виду поля микроскопических смещений подрешеток. Тем не менее приведем общее решение уравнения (2.7), которое может быть найдено при произвольных граничных условиях, задаваемых константами u_s и G ,

( к / 2)^{v 2} u , x = 1 / R ( u ) ,                                         (2.14)

где дается R ( u ) выражением (2.13). Опуская выкладки, пишем решение в окончательном виде

. /         sn[xK(v)/H]                              _ , _ sm(u 2) = 9 г ( ) J !.                            (2.15)

• ^{V z} ’ 1 + g ²cn[ xK ( v )/ H ]

• 3.    Однокомпонентные двумерные поля.

Здесь sn(.) и cn (.) - эллиптические функции синуса и косинуса, K(v) - полный эллиптический интеграл первого рода, v - его аргумент (модуль), равный v2 = (1 + g2/c2)/(1 + g2)«1 - G(P - 252/X)/P(G + P); (5 ^ 0).      (2.16)

При выводе формулы (2.15) воспользовались определением полного интеграла первого рода K ( v ) = F ( n /2, v ), из которого следует так называемое дисперсионное соотношение

K ( v ) = H [(1 + g ') G / 2 к ] 1 / ² .                            (2.17)

Основные уравнения

Рассмотрим более сложный случай однокомпонентных, но двумерных полей:

U i ^ U_z ( x , y ) ,      U i ^ U z ( x , y ) , F z ( u ) = p sin u_z ; u ² = u a-' u_k ,

U x ,= U y = u x = u y = F x = F y = 0.                       (3.1)

Этот случай удается проанализировать точно до конца для кристаллов всех классов симметрии, исключая триклинную и моноклинную сингонии. Решения вида U z ( x , y ), u z ( x , y ) описывают, очевидно, деформации в плоскости ( x , y ), когда смещения происходят вдоль перпендикулярной оси.

Этот случай реализуется в случае возникновения так называемого «реечного» мартенсита. Другим примером может служить реконструированная (несингулярная) поверхность монокристалла, на которой возникают ступеньки, выступы, террасы и другие дефекты, возникающие при отжиге (в результате выхода дислокаций), деформировании и формировании свободной поверхности в результате косого среза. Весьма интересен случай возникновения негладкого фронта упруго-пластической ударной волны, сопро- вождаемой эффектом дисперсии поля продольных скоростей [6]. Примеры подобных решений ниже приводятся.

Продолжим пока что общий анализ. В силу условия u x = u_y = 0 имеем u а - 1 u_k = u ^ . Тогда Ф ( u_R ) ^ (1 - cos u_z ) и для последних пяти классов симметрии энергия деформаций и структурных изменений (1.3) примет (с учетом введенных ограничений) вид

D = £ [7( ^ 1 U x ' X U 2у ) + Г⁽ k u* x + k 2 <у ) + ( p - S U . , x - S U . , У )(1 - cos " , )] dxd. • (3-2)

BH ^V 22

Для ромбической сингонии X 1 *X ₂ ; k 1 * k ₂ ; S 1 * S ₂, для 4 классов более высокой симметрии эти константы попарно равны. Используя это выражение как слагаемое в лагранжиане, получим вариационные уравнения движения

Р Uz = CTzx,x +°zy,у ;

РUz = ki uz,xx + k2 uz.. -(p-S1 Ux -S2 Uz.)srnuz.

В первом уравнении введены обозначения ст zx = X1 U x + S1(1-cos uz), CT zx = X1 U x + S1(1-cos uz).(3.5)

Величины, стоящие слева в этих выражениях, будем называть напряжениями.

Используя последние выражения, исключим из уравнения для микросмещений (3.4) макроградиенты Ux,Uy, выразив их через напряжения. Получим уравнение микрополя в окончательном виде цй’ = k u, vv + k u,,-Psinu, + (S,2/X, + S2/X.)sinu, cosu,.(3.6)

z 1 z ,xx      2 z ,УУ                z 1 1      2 2          zz

Здесь введено обозначение для эффективной величины межатомного барьера (половины энергии активации)

P = pв; в = (1 -S1 стzx/pXx -S2 ctzy/pX2).(3.7)

Здесь в - бифуркационный параметр

Вместе с уравнением (3.3) получим систему двух уравнений относительно напряжений и микросмещений. Она удобна при анализе влияния постоянных напряжений на бифуркации решения уравнения (3.6). Поскольку постоянные напряжения являются частным решением уравнения (3.3), их величину можно выбирать произвольно, сообразуясь лишь с граничными значениями. Тогда поправка к величине эффективного потенциального барьера 2P может принимать различные значения в зависимости от соотношения компонент тензора напряжений. Удобно воспользоваться полярными координатами ( ст, а) в плоскости компонент напряжений, положив ctz =ст cos а; ctz = ст sin а; ct = Jct2 +ст2 .                      (3.8)

zx                        zy                                zx zy

Тогда (3.7) запишется в виде

P = p -сту cos( а-а o ) ; у = ^S 1² /X 2 + S ₂ ² /X 2 ; у cos а o = S 1 X 1;y sin а _o = S ₂ X ₂. (3.9)

Здесь и далее ст ² - это второй инвариант тензора напряжений.

Поправка к величине естественного барьера p линейна по напряжениям и угол аo + п/2 задает наклон соответствующей линии пропорционального нагружения в плоскости напряжений. Интересно, что поправка может быть равна нулю ( P = p ) и при отличных от нуля напряжениях, компенсирующих друг друга. Это имеет место при сложнонапряженном состоянии, когда а = ao + п/2, т.е. при условии о zxSi !\ + о zyS 2 /Х2 = 0. (3.10)

В этом случае (нулевого эффекта напряжений) соотношение между компонентами тензора напряжений и наклон соответствующей линии нагружения определяются только материальными свойствами тела. Эта линия проходит через начало коорди-^нат( о zx = 0 ,о zy = 0).

Напротив, напряжения оказывают наибольшее влияние, когда поправка достигает максимального значения, равного p . При этом P = 0 и согласно (3.9)

оу cos( a-a o ) = p . (3.11)

В результате достигается граница бифуркации, и решетка теряет устойчивость – происходит скачкообразная смена решения уравнения (3.6), в котором исчезает нелинейное слагаемое, пропорциональное барьеру P.

Прямолинейная граница, задаваемая уравнением (3.11), параллельна линии нулевого эффекта напряжений (3.10), но удалена от нее на «расстояние» о _b = p /у , соответствующее минимальной длине радиус-вектора с наклоном a = a _o .

Учитывая ограниченность косинуса в (3.11), можно записать критерий бифуркаций в более простой форме

о>о b; о b = p /у. (3.12)

Ясно, что когда второй инвариант тензора напряжений достигает критического значения, равного о 2 , напряжения полностью «подавляют» естественный барьер.

Заметим, что поправка к естественному потенциальному барьеру p может достигать и отрицательного значения (при a = a _o + п ), равного - оу . Тогда напряжения, напротив, увеличивают эффективный потенциальный барьер, повышая прочность решетки.

Таким образом, бифуркационная граница (3.11) делит всю плоскость напряженного состояния на две части. Если выполняется условие (3.12), то в уравнении (3.6) сохраняется знак перед нелинейным синусоидальным слагаемым (с множителем P ), чему отвечает одно семейство решений – с большой амплитудой, скажем, забегая вперед.

Если переменить в критерии (3.12) знак неравенства на противоположный, то и в уравнении (3.6) произойдет смена знака. Будет показано, что соответствующий переход через точку бифуркации приведет к другой структуре, описываемой другим решением. Это будет рассмотрено далее подробно.

Возвратимся к общему анализу уравнения (3.6). При этом следует признать, что аналитическая форма решений для двумерного уравнения может быть установлена в частных случаях, например, при малых значениях коэффициентов стрикции. Отметим, что это условие плохо выполняется вблизи точки бифуркакции P =0. В этом случае в уравнении (3.6) будем пренебрегать последним слагаемым и решать в нулевом приближении уравнение

Ц U z ~ k 1 ^uz , xx ^{+ k} 2 u z , yy ^- P sin u z • ⁽3.¹³⁾

Это уравнение поддается точному анализу. В частности, можно найти в явном виде целый набор его частных решений, обладающих интересным физическим смыслом, и проанализировать как вопрос об их устойчивости вдали от точки бифуркации P = 0, так и вопрос о переходе через нее.

В частности, сразу же можно установить связь между его решениями, разделенными точкой бифуркации P=0. При переходе через нее, очевидно, меняется знак перед нелинейным слагаемым в уравнении (3.13). Поскольку функция синуса меняет знак при замене и на и ± п (в действительности, на целое число п), то решения до точки бифуркации (и - ) и после нее (и+ ) связаны очевидно соотношением и " = и +±п,                                  (3-14)

т.е. испытывают при переходе соответствующий разрыв. Эти решения удовлетворяют, таким образом, разным уравнениям.

В силу соотношения (3.14) достаточно найти лишь одно из решений. Из всего сказанного следует весьма важное простое свойство бифуркационного перехода. Переход от допороговых напряжений к запороговым (или изменение знака P ) приводит согласно (3.14) просто к сдвигу микросмещений на половину периода, т.е.коллективному переходу атомов в соседние ячейки.

Поверхностные микроструктуры в статике. Реконструкция поверхности

Динамическое уравнение (3.13) переходит в статике в уравнение синус-Гельмгольца

(3.15)

0 = клН + kk₇u - рP sin и . 1 z , лл        z. z , yy                   z

Здесь P определяется в новых обозначениях в (3.8). Нелинейное уравнение (3.15) содержит две характеристических длины когерентности подрешеток:

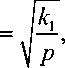
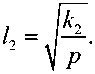
(3.16)

Они определяют те мезоскопические (промежуточные) масштабы длин, в пределах которых подрешетки остаются (несмотря на микроградиенты) когерентными, строго говоря, конгруэнтными, т.е. могут быть совмещены жестким сдвигом. Это характеристики микроскопического поля, в противоположность макроскопическому безмасштабному полю. Формально, если длина 1 1 ^ 0, приходим к известной одномерной модели Френкеля – Конторовой, или цепочке атомов на жесткой периодической подложке.

Микроструктуры с сингулярными дефектами

Поиск частных решений этого уравнения в явной форме опирается на метод разделения переменных Лэма [7], который нуждается в некоторой доработке, поскольку не позволяет выявить весьма важные дисперсионные соотношения. Это было сделано в работах [8]. В результате можно построить 32 частных решения, имеющих различный физический смысл, который уточняется при анализе дисперсионных соотношений.

Легко видеть, что уравнение (3.15) не имеет однородных решений кроме тривиальных (нулевого и целочисленного), когда подрешетки смещаются в кристаллографически эквивалентные положения. Среди неоднородных решений особый интерес представляют двоякопериодические, поскольку они характеризуются ограниченным масштабом неоднородности.

Начнем анализ с решения уравнения (3.15). Возникновение дефектов свяжем с возможностью фрагментации решетки – возникновением доменной структуры, когда непрерывные поля смещений возникают в ограниченных областях с линейными масштабами H и B , разделенных границами, несущими сингулярные дефекты – микропроскальзывания атомов. Ясно, что соответствующее частное решение должно носить двоякопериодический характер.

Рассмотрим случай, который определим формально с помощью нижеследующих условий на параллельных эквидистантных линиях скольжения x =const, или внутренних границах системы плоскопараллельных горизонтальных слоев толщиной 2 H и на поперечных границах ячеек y =const.

Нужное решение можно построить, потребовав чтобы на границах слоев взаимное проскальзывание соседних атомов вдоль оси OZ , достигающее по абсолютной величине наибольшего значения, было равно величине межатомного расстояния. Внутри слоев оно, разумеется, меньше - в результате имеем условие u_z <  1. При этом микропроскальзывания должны носить знакопеременный периодический характер при переходе от одного полудомена (шириной 2 B ) к другому, т.е.

u ( H , у ) =+ 2 п, и _ (0 , у ) = 0 , u_z ( - H , у ) = - 2 п, (0 <  у <  2 B )

(3.17) uz (H, у) = -2п, uz (0, у) = 0, uz (-H, у) = +2п, (-2B < у < 0).

Эти условия должны повторяться вдоль оси OX с периодичностью 2 H и вдоль оси OY с периодичностью 4 B . Ясно, что микропроскальзывания достигают наибольшей величины, равной величине периода (или целому числу периодов!), на указанных доменных границах, а внутри слоя оно меньше, т.е. u_z <  2 п . Там, где u_z < п (потенциальные межатомные барьеры не преодолеваются), возникают чисто упругие микродеформации. В соответствующей упругой зоне домена энергия накапливается, а в пластической происходит ее сброс. В целом же в решетке развиваются упруго- пластические микродеформации, приводящие к оптимизации системы, если она первоначально испытывала большие однородные макродеформации.

Решение уравнения (3.15), подчиняющееся этим граничным условиям, удобно строить, используя метод разделения переменных Лэма [7,8], который в конечном счете, приводит к выражению

⁽ u ; / 4) =± a

tn( xK 1 / H ) sn( уК ₂ / B ) ’

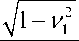
^v- 2

(3.18)

Смысл дополнительного верхнего значка «минус» означает, что решалось уравнение (3.15) с соответствующим знаком перед синусом. Это необходимо для дальнейшего. Здесь величина a формально рассматривается как амплитуда микродеформаций. Два знака справа в (3.18) соответствуют двум эквивалентным направлениям сдвига вдоль оси OZ. Далее, 2H и 4B являются периодами стоящих справа функций, т.е. эллиптического тангенса (tn) и эллиптического синуса (sn). Величины K1 и K2 представляют собой полные эллиптические интегралы первого рода, зависящие от своих модулей v1,v2 известным образом [9]. Их значения укладываются в интервал от нуля до единицы. Все двумерное множество их значений (констант интегрирования) составляет область существования семейства решений вида (3.18). Она изображена на рис.3. От- сюда видно, что эллиптические интегралы K1, K2 определяют эллиптические же пространственные частоты, или градиенты микродеформаций. Величины же 1/Н и 1/В определяют средние частоты. Ясно, что первые становятся весьма большими при значениях модулей, близких к единице.

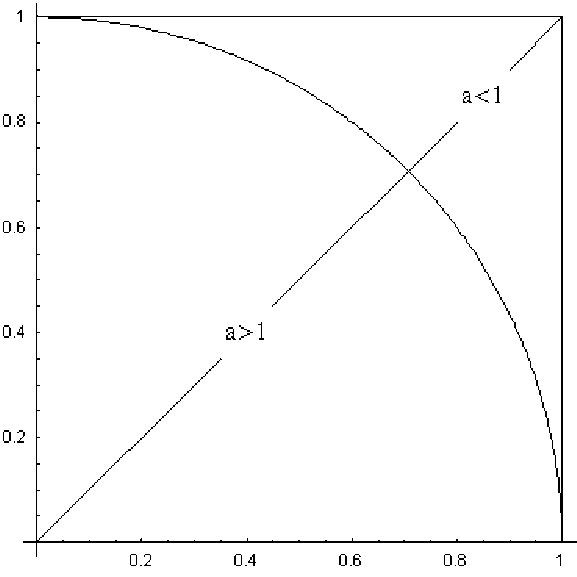
Рис.3. Область значений произвольных параметров v1,v2 с круговой границей бифуркации и двумя подобластями неупругих (а > 1) и упругих (а < 1) деформаций

Используя свойство эллиптического тангенса tn0 = 0 и tn K ^ да [9], можно видеть, что решение (3.18) удовлетворяет граничным условиям (3.17). Очевидно, что оно подчиняется и периодическим (вдоль и поперек слоя) условиям с периодом 4 В и 2 H соответственно. В результате имеем двоякопериодическое решение, которому соответствует двоякопериодическая суперструктура деформированной решетки. Исходная трансляционная симметрия решетки нарушена микродеформациями лишь отчасти. Произошло огрубление ее масштабов – от размеров ячейки до размеров фрагмента B , H . Фактически мы получили решение для всего пространства. Введенные нами ранее формально границы имеют смысл не внешних, а внутренних границ, возникающих под воздействием больших макроскопических напряжений или деформаций.

Что касается поперечных доменных границ, то при условии y = (2 r + 1) B , r = + 0 , 1 , 2 ,... , когда левая часть решения (3.18) обращается в бесконечность, имеем вертикальные ряды солитонов Френкеля – Конторовой (дислокаций несоответствия). Действительно, рассмотрим окрестность начала координат. Тогда эллиптические тангенс и синус в линейном приближении дадут следующее выражение для формулы (3.18):

x tg(Uz/4)« (-^2) = ( -2)ф. (3.19) z yk 1 k1

Здесь ф — угол локальной полярной системы координат. Очевидно, поле микросмещений в окрестности начала координат является многозначной функцией, зависящей от числа обходов вокруг него по замкнутому контуру. Тогда u_z / 4 = arctg( 4k ₂ ф/ 4k 1 ), т.е. получаем топологический дефект поля u_z с положительным (отрицательным) зарядом.

Весьма существенно то, что в формуле (3.19) в отличие от (3.18) отсутствуют амплитуда и масштабы фрагментов (расстояния между дефектами). Следовательно, последняя формула описывает универсальное ядро единичного дефекта, в то время как (3.18) учитывает и взаимодействие дефектов.

Такие дефекты (заряды) возникают в каждой точке, которая является одновременно нулем тангенса ( x = 0 , 2 H , 4 H , ...) и синуса ( у = 0 , 2 B , 4 B,... ). При этом знаки зарядов чередуются вдоль горизонтальных слоев, но сохраняются вдоль вертикальных. На рис.4 показан поверхностный микрорельеф, образованный микросмещениями атомов ортогонально плоскости ( XY) в соответствии с полем микросмещений u_z ( x , у ), согласно решению (3.18).

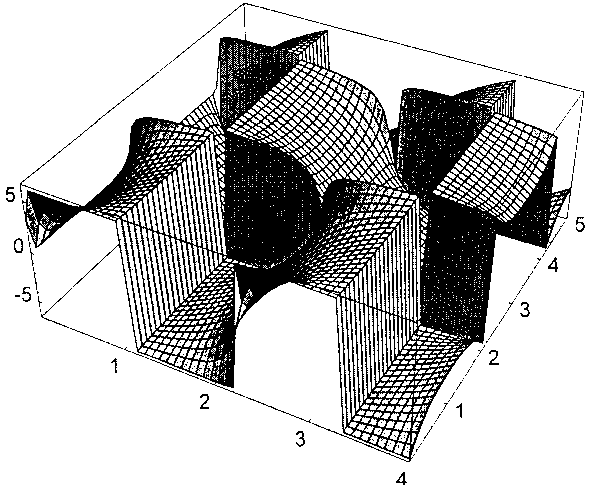
Рис.4. Микрорельеф поверхности, описываемый сингулярным решением (3.18)

Таким образом, настоящая теория позволяет описывать зарождение сингулярных дефектов в первоначально идеальной решетке и ее фрагментацию – разделение на блоки. Оценки показывают, что они имеют микроскопические, а при больших напряжениях и наноскопические масштабы.

Локальная устойчивость системы дефектов

Периоды суперструктуры (расстояния между дефектами) не произвольны. Они зависят от свойств решетки и градиентов микродеформаций, а также от макродеформаций, играющих роль внешнего поля. Ограничения, связанные со свойствами и градиентами, следуют из дисперсионных соотношений, которые получаются, если подставить (3.18) в уравнение (3.15). После элементарных преобразований получим

eH2 = (1 - a2)(1 - а2 V2)K2; H2 = H2//1;

в B ² = (1 - а ²)(1 - а ² v 2 ) K ₂ ² / а ² ; в ² = B² / / ₂-                   (3-20)

Здесь в - бифуркационный параметр (3.7), который в новых обозначениях (3.8) можно записать так:

р=1-°cosa-aо)/°ь; 0=^1 +02, .                 (3.21)

Дисперсионные соотношения связывают параметры v 1 ,v ₂ (т.е. градиенты микродеформаций) со свойствами решетки, масштабами ансамбля дефектов H и B , а также величиной a , которую будем называть амплитудой микрополя. Они задают область существования решения.

Дальнейшие ограничения выявляются, если исключить из этих соотношений константы интегрирования v 1 ,v ₂. Поскольку амплитудный параметр а согласно определению в (3.18) является их функцией, можно вначале исключить, скажем, величину v 1 , выразив эту последнюю через а и v ₂. Тогда, зафиксировав а , получим два уравнения (3.20) для двух переменных B , H с одним переменным параметром v ₂. Исключая и его из этих двух уравнений, получим связь между B и H при заданном амплитудном параметре а . Взаимосвязь трех величин а , B , H может быть представлена семейством кривых, выражающих зависимость H от B для разных значений параметра a .

Семейство показано на рис.5. В этом случае каждая кривая на той же плоскости ( HB ) при заданном значении а <  1 имеет по одной асимптоте - вертикальной B = B t и горизонтальной H = H t , так что

H_t <  H <» , B ^ B_t .                      (3.22)

Асимптоты (горизонтальные и вертикальные) видны на рис.5. Значения этих пределов

H t = (1 - а ² ) K (V ,) Л/р.    2 B t =п 7 а "² - 1 ф; v, = 71^ 0 4 .       (3.23)

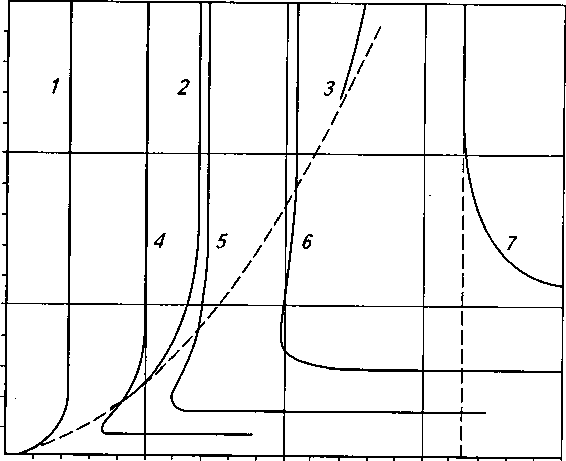
о               0,5            1,0            1,5            В

Рис.5. Взаимосвязь масштабов двухмерной наноструктуры при заданной амплитуде a равной 1,01(1), 1,11(2), 2(3), для упруго-пластических доменов (с нижней границей – пунктирная кривая). Упругим доменам отвечают значения амплитуды: 0,95(4), 0,99(5), 0,83(6), 0,71(7)

Очевидно не все значения параметров H , B допустимы - из полученных соотношений следуют явные ограничения. Они задают предельно малый размер домена, возникающий при заданных амплитуде и напряжениях: H_tB_t <  HB . Отметим, что отношение размеров (анизотропия фрагмента) не зависит от напряжений - бифуркационный параметр в сокращается.

В области же a >  1, каждая кривая на той же плоскости ( HB ) при заданном значении a <  1 начинается из точки H = H c , так что

B >  B c ; H >  H c ; (3.24)

H c = ( п/ 2)( a ² - 1) / a Т-Р; B c = ( a ² - 1) K ( a "² ) Z a ² 7—1 • (3.25)

Начальные точки этих кривых H c , B c лежат на пунктирной огибающей, показанной на рис.5. Эти соотношения определяют предельно малый размер домена, возникающий при заданных амплитуде и напряжениях: H_cB_c <  HB . Так же, как и в предыдущем случае, отношение размеров (анизотропия фрагмента) не зависит от напряжений - бифуркационный параметр Р сокращается.

Заметим, что дисперсионные соотношения получены впервые в наших работах [8,10,11]. В работах Лэма и его последователей они не вводятся ввиду сокращенного числа произвольных констант, фигурирующих при построении решений. В нашей процедуре решения дополнительно зависят от двух констант интегрирования ( v 1 ,v ₂), которые дисперсионными соотношениями связываются с размерами доменов H и B . Поэтому формула (3.18) в нашей теории задает целое семейство частных решений в области этих параметров, показанной на рис.3.

Поскольку в дисперсионные соотношения (3.20) входят (в качестве параметров, влияющих на выбор характеристик структуры H , B или v 1 ,v ₂) также и напряжения (через бифуркационный параметр), от величины и знака которых зависит выбор констант интегрирования, область существования решения, целесообразно рассмотреть оба случая последовательно.

Перестройка структуры при критических напряжениях

Рассмотрим вначале случай Р >  0, когда напряжения ниже пороговых ( о < о b ). Напомним, что о ² означает второй инвариант тензора напряжений. В этом случае дисперсионные соотношения непротиворечивы (решение существует), если a <  1 - правые части положительны. Этому неравенству отвечает часть прямоугольной области констант интегрирования, показанной на рис.3 - за пределами круговой границы v ^ + V ² >  1.

Если же Р <  0 ( о > о b ), то дисперсионные соотношения непротиворечивы и решение (3.18) существует при a >  1, т.е. внутри области v² + v 2 < 1. Условие a = 1 или о = о b определяет бифуркационную границу v² +v 2 1, показанную на рис.3.

Таким образом, микрополе в обеих областях задается одинаковой зависимостью (3.18), но амплитудный множитель a в разных областях принимает различные значения. Подчеркнем, что этот переход имеет место, если изменение знака бифуркационного фактора Р сопровождается одновременным изменением и знака амплитудного множителя (1 - a2) или переходом в другую область существования решения, т.е., по суще- ству, к другой микроструктуре. Этот переход можно описать явной зависимостью вида a = a (ст) , показывающей изменение амплитуды решения от внешнего напряжения.

Рассмотрим вначале область допороговых напряжений, когда a <1. Найдем эту зависимость для предельно малого фрагмента, с площадью 8HtBt. Используя формулы (3.22), пишем в t = п(1 - a 2) K (vt) V a -1, в t = H,B, в, v 2 = (1 - a4).            (3.26)

Эта зависимость представлена на рис.6 нижней ветвью кривой, исходящей из точки бифуркации р t = 0 и показывающей, какие микроструктуры минимального масштаба возникают с ростом напряжений, вплоть до значения амплитуды, равной 1, за пределами которой возникают уже иные структуры.

Рассмотрим их образование. В области a > 1 напряжения превышают пороговые. В этом случае минимальный размер фрагмента 8HcBc задается соотношением рcHcBc =-(a2 -1)2 K(a-2)Z2a3/п, рc=рHcBX,              (3.27)

здесь бифуркационный параметр становится отрицательным, т.е. положительна разность -P = ст cos( a - a o ) /ст b - 1. Соответствующей зависимости a = a ( P ) отвечает на том же рис.6 верхняя ветвь. Обе ветви разделены одной точкой бифуркации a = 1 , P = 0, где р _c = р t .

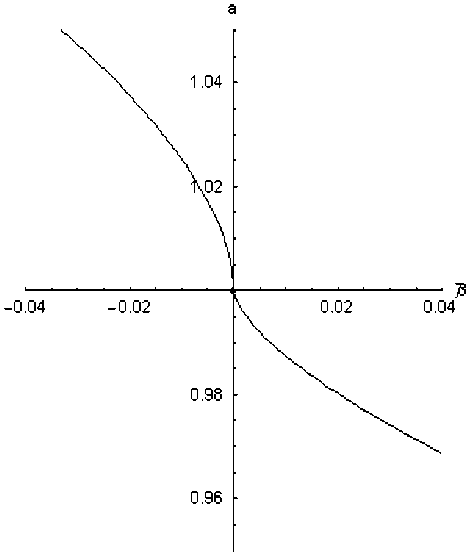
Рис.6. Зависимость амплитуды сингулярного микрополя (3.18) от внешних напряжений с точкой бифуркации при a = 1

Обращает на себя внимание универсальность бифуркационного комплекса р -абсциссы точек демонстрируемых кривых. Для фиксированного размера фрагмента эти кривые показывают зависимость амплитуды микрополя от напряжений (содержащуюся в бифуркационном параметре) – с точкой бифуркации в нуле. Если напряжения равны нулю, то эти кривые показывают зависимость от амплитуды величины двухмерного

Сильно нелинейная теория упругих и неупругих деформаций кристаллических тел объема фрагмента с точкой перехода в область неупругих деформаций, которой отвечают бесконечно мелкие фрагменты. При равных нулю напряжениях, когда в = 1, получим формулу, связывающую площадь фрагмента с соответствующей начальной амплитудой a_o ,

H , B , =п (1 - a ; )K ( v , ) V a - - 1. (3.28)

Это значит, что соответствующая микроструктура возможна и в отсутствие напряжений.

Как уже отмечалось, изменение знака перед синусоидальным слагаемым в уравнении (3.15) приводит к решению, сдвинутому на π (на половину периода решетки) согласно соотношению (3.13). Тогда в одной и той же области должны существовать две формы решения, отвечающие одному и тому же уравнению (3.15). Так, анализируемое решение u - ( x , у ), отвечающее формуле (3.18), имеет место при условии a >  1 и в <  0. Второе решение u ^ ( x , у ) отвечает формуле (3.14) при условии a >  1 (т.е. в той же области), но при условии в >0. Поэтому ответ на поставленный вопрос таков. Переход в область запороговых напряжений и больших амплитуд можно рассматривать также и как увеличение микросмещений на половину периода согласно (3.14). Ясно, что при этом неизбежно происходит спуск атомов в соседние ячейки, сопровождаемый неупругими деформациями.

Глобальная устойчивость системы дефектов в отсутствие внешних напряжений

Существование неоднородных микроструктур в ненагруженном кристалле, связанных с внутренними напряжениями, вызванных дефектами, является неоспоримым фактом. Поскольку они предсказываются в данной теории, целесообразно поставить вопрос об их устойчивости. Каждое решение типа (3.18) предполагает целую область произвольных констант интегрирования, поэтому возникает вопрос, при каких значениях параметров v 1 , v ₂ или масштабов H и B данная спонтанная микроструктура достигает минимума энергии. Реальный кристалл, содержащий дефекты, обладает, конечно, более высокой энергией, чем его прообраз, лишенный дефектов. Тем не менее кристалл с дефектами относительно устойчив, и время жизни дефектной структуры может быть очень велико. Его можно сократить за счет повышения температуры и путем выдержки при повышенной температуре (отжиге) наблюдать его переход в более стабильное бездефектное состояние, не подвергая его внешнему силовому воздействию. Имея это в виду, разумно выяснить, какие микрополя наиболее устойчивы в отсутствие внешних напряжений, когда эффективная энергия активации межатомных связей оказывается равной своему естественному состоянию, т.е. когда выполняется условие P = p .

Для этого необходимо исследовать экстремумы макроскопической плотности энергии D при заданных граничных условиях. В общем виде для двухмерных полей это сделать невозможно, однако для частных (явных) решений уравнения (3.15) интеграл D находится и задача решается. Удобно соответствующее выражение (3.2) переписать, заменив макроградиенты смещений на напряжения согласно (3.5). Получим

D = le pBH ^ ( ' ^V: x ' ' ) dxdy ⁺ D . (3.29)

Здесь выделилась составляющая – плотность энергии дефектов

^{1  1} 22        ¹ 22      2

(3.30)

D = o _D^J,z^[7^{( k}1 u z , x ⁺ k 2 u z , y ) + P ⁽¹ - cos u z ) -- ^{( S} 1 /^ 1 — ^S 2 /^ 2 ) ⁽¹ — cos u z ) 1 dxdy ■

8 pBH ^V 2                           2

Интерес представляют экстремумы функции энергии дефектов D . Последняя поддается прямому вычислению, если используется явная форма решения для микрополя. Решение (3.18) было получено в пренебрежении квадратичными слагаемыми ( S ² ), принимая коэффициенты стрикции малыми. Тогда следует принять, что

D «

¹       [¹( k

8 pBH ^V 2 ¹

u_z² x + k 2 u 2 _y ) + P (1 — c^os u_z )1 dxdy ■

(3.31)

Найденная в этом приближении функция плотности энергии дефектов D( v 1 ,v ₂), заданных решением (3.18), показана на рис.2. Она представлена как функция произвольных параметров интегрирования v 1 , v ₂, которые согласно (3.22) однозначно связаны с пространственными частотами. Поэтому можно говорить о распределении энергии по спектру пространственных частот. Можно прейти и к средним частотам (1/ H ,1/ B ) или линейным плотностям дефектов. Если напряжения равны нулю, то P = p , т.е. потенциальный барьер перестройки решетки фиксирован и нами не управляется. Тогда распределение D ( v 1 , v 2 ) показывает просто, какая микроструктура наиболее выгодна и потому может реально существовать, возникнув в предыстории материала. Если речь идет о решении в области пространственных частот v 1² +v 2 > 1 или a<1, то точка наименьшего значения энергии определяется значениями констант интегрирования v 1 ^ 1 , v ₂ ^ 1. Точное значение энергии не считается. Удается приблизиться к значению D = 1,56 при значениях v 1 = 0 , 9999 , v ₂ = 0 , 9999 . Им отвечают следующие относительные размеры: H =5,56; B =46,80.

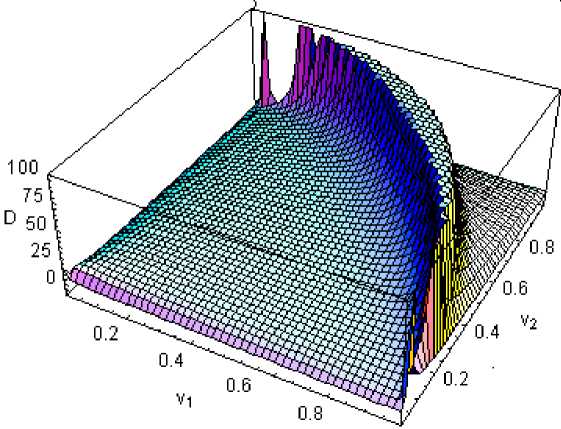
Рис.7. Распределение плотности энергии сингулярной микроструктуры (3.18) по области произвольных параметров интегрирования с логарифмической расходимостью на круговой бифуркационной границе перехода от упругих к неупругим деформациям

Эта структура или близкая к ней должна быть устойчивой. Как видно из рис.7, распределение энергии D ( v 1 , v ₂) по области частот v 2 + v ₂ >  1 (или a <1) ограничивается высоким барьером по круговой границе сектора a =1, которая является условием бифуркации решений уравнения (3.15). Вторая ветвь решения ( a >1) отличается в соответствии с (3.18) сдвигом микрополя на величину –π, т.е. на половину периода решетки. Эти структуры отвечают высоким упругим энергиям и без внешних напряжений не возникают, оказываясь неустойчивыми. Уже самая малоэнергоемкая из них ( v 1 = v ₂ = 0 ; H = 49 , 62 , B = 1,57) требует пороговых затрат энергии D = 16,69, которые могут быть реализованы за счет работы внешних напряжений.

Другие системы дефектов

Рассмотрим пример другой микроструктуры, возникающей как в отсутствие, так и при наличии внешних напряжений. Это так называемые модулированные структуры, наблюдающиеся при распаде упорядоченных многокомпонентных твердых растворов (сплавов) и блок-сополимеров. Они, в отличие от предыдущих случаев, не связаны с сингулярными дефектами, и энергия D(v1,v2) также несингулярна. Соответствующие размытые дефекты представляют собой просто неоднородности в пространственном распределении атомов. Их называют повреждениями и с ними связывают эффекты разрыхления структуры. Используя методику разделения переменных, можно получить так же, как и выше, семейство решений вида tguz(x,y)/4 = a dn(xK2/H); a4 = (1 - v2)/(1 -v22),             (3.32)

^dn( У ^к 2 / ^B )

а также дисперсионные соотношения в H2 = a -2(1 + a2 )[1 + (1 - v2) a2 ] K12;                         (3.33)

в B ² = a '(I + a ²)[1 + (1 -v 2 ) a ²] K ₂ ² .                         (3.34)

Соответствующая структура – микрорельеф поверхности несколько напоминает картину рис.4, но вместо резких выступов на поверхности, описываемых решением (3.18), здесь возникают гладкие «холмы».

Здесь так же, как и в случае микрополя с дефектами, существуют две области возникновения предельно малых двухмерных нанообъемов H _m B _m в зависимости от амплитуды и от внешних напряжений. Однако они разделены не точкой бифуркации.

Дело в том, что правые части дисперсионных соотношений (3.33), (3.34) определенно положительны. Поэтому решение (3.32) возможно лишь при наличии внешних докритических напряжений, стабилизирующих структуру, когда бифуркационный параметр в не обращается в нуль, а остается положительным. Однако бифуркационный параметр должен превышать некоторое конечное пороговое (но не критическое !) значение, зависящее от амплитуды и масштабов H , B . Действительно, существуют пороговые структуры. Так, при условии v 1 = 0, согласно определению амплитуды в (3.32), a ⁴ = 1 / (1 -v 22 ) > 0 и дисперсионные соотношения принимают вид

H m в=п 2 (1 + a ²) ² / 4 a ⁴; B ²„ ₽= (1 + a ²) ² / a * K ² ( v , , ) , v , 1 = 4 1 - a .      (3.35)

Здесь Hm < H, Bm < B представляют собой наименьшие масштабы, возможные при данной амплитуде a . Интерес представляет их произведение – площадь минимального фрагмента, которая согласно этим формулам следующим образом выражается через амплитуду и бифуркационный комплекс:

в = (1 + a ²) 2 K ( v _с 1) / 2 a ⁴ п; в = Н т В т в^ .                (3.36)

Заметим, что отношение масштабов (анизотропия формы фрагмента) не зависит от бифуркационного параметра, а значит, и от напряжений. Это значит, что структурные переходы касаются лишь размеров фрагментов или плотности дефектов.

Самый наименьший размер минимального фрагмента B mm H mm = п ² достигается при наименьшей же амплитуде, равной a = 1, что легко проверить непосредственно. Эта величина и определяет порог зарождения наноструктуры. Действительно, при условии a >  1 из (3.36) получим неравенство в >  1. На рис.8 зависимость амплитуды а (микрополя с минимальными фрагментами) от в , а значит, и от напряжений, показана нижней ветвью кривой, исходящей из пороговой точки (1,1).

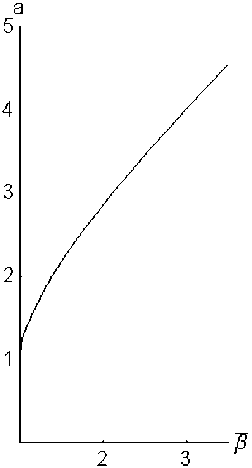
Рис.8. Зависимость амплитуды бездефектного микрополя (3.32) от напряжений.

Точка бифуркации отсутствует

Вторая ветвь минимальных фрагментов получается при v2 = 0, a4 = 1 - nu^ < 1. Тогда дисперсионные соотношения (3.33), (3.34) дают соответствующую зависимость в виде в=[(1 + a2)/пa2]K(vc2), vc2 = V1 - a4 .                     (3.37)

Она представлена на рис.8 верхней ветвью, которая исходит из той же пороговой точки a = 1 , в = 1 и также распространяется вправо.

Единый критерий зарождения микроструктур ( в >  1), описываемых решениями семейства (3.32), полезно переписать следующим образом:

о co^s( a^-a о ) ° ь < ^{1 -}п ² / H m B m .                     ⁽3.3⁸⁾

В случае предельно мелких фрагментов ( H_mB_m = п ² ) справа здесь получается нуль и (3.38) является уравнением прямой, проходящей через начало координат в плоскости напряжений под углом а _о + п/ 2 .

Этот критерий существования наноструктуры, безусловно, выполняется, если косинус слева отрицателен, т.е. в случае любых сжимающих напряжений. Однако он реализуется и при небольших положительных (растягивающих) напряжениях, когда их относительная величина укладывается в диапазон от 1 до 0.

Оба предела имеют смысл. Если отношение равно 1, то достигается точка бифуркации (в = 0) и потенциальный барьер преодолевается ( P = 0). Если при этом все же величина комплекса в конечна, то может возникать структура с неопределенно большими масштабами H и B . Действительно, в этом случае в формуле (3.32), описывающей эту структуру, можно положить аргументы в эллиптических функциях справа равными нулю. Тогда сами эти функции (dn()) обратятся в 1, а решение примет вид tg( и / 4) = a . Это значит, что поле микросмещений постоянно в пространстве. Используя определение амплитуды a , легко видеть, что происходит жесткий сдвиг подрешеток на величину от π до 2π (от половины до целого периода решетки), поскольку параметры v 1 ,v 2 изменяются в пределах от нуля до единицы. Заметим, что при жестком смещении подрешеток в неограниченном пространстве сдвиг на 2π (на один период) равнозначен нулевому сдвигу. Однако при наличии границ тела сдвиг на 2π приводит к образованию на ней неровности, сопровождаемой линией скольжения. Этот процесс и требует достижения порогового значения напряжения, о котором шла речь выше.

Другой крайний случай – обращение в нуль внешних напряжений. Критерий (3.38) также имеет смысл и определяет наименьшую величину двухмерного объема фрагмента ( H m B m = п ² ) в качестве начального зародыша, который существовал в теле в отсутствие напряжений.

Заметим, что в отсутствие внешних напряжений устойчивость масштабов этой наноструктуры, возникающей спонтанно, обеспечивается минимальностью ее энергии D как функции параметров v 1 , v 2 . Это распределение показано на рис.9. Здесь энергия имеет точку наименьшего значения в правом верхнем углу области ( v 1 = 0 , 999 , v 2 = 0 , 999).

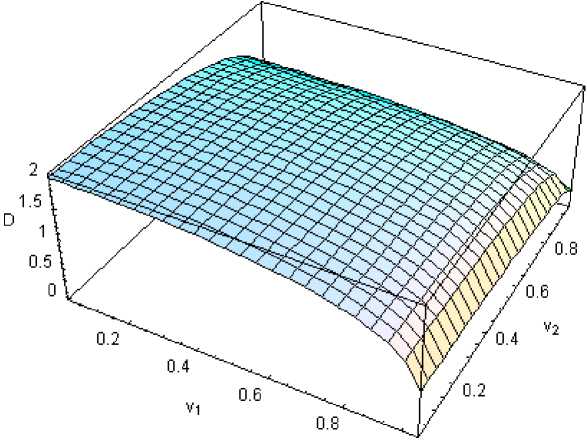
Рис.9. Распределение плотности энергии бездефектной микроструктуры (3.32) по области произвольных параметров интегрирования в отсутствие перехода от упругих к неупругим деформациям

4.    Двухкомпонентные поля в кристаллах кубической симметрии

Ограничимся кристаллами кубической симметрии. Тогда, учитывая соотношения (1.12), запишем уравнение (1.15) в более простой форме

H Ш = kkmnuk, mn - PL sin uR , uR = u / a .(4-

Свернув это уравнение с ортом вектора микросмещений и производя элементарные операции, можно переписать это векторное уравнение в виде двух уравнений

H Lj Hj = Lj kjkmn Uk,mn - P sin uR ,

H u i - H Li Lj U j = kamn uk,mn - ^i Lj kjkmn Uk,mn "

Последнее векторное уравнение эквивалентно двум независимым, поскольку его свертка с ортом L_i дает тождество.

Двухкомпонентные двухмерные микрополя

Введем еще одно упрощение. Рассмотрим плоскую задачу, положив для полей смещений

U x = U x ( x , y ) , U y = U y ( x , y ) , U z = 0 ;

U x = U x ( x , y ) , U y = U y ( x , y ) , U z = 0 .                            (4.4)

Поля напряжений примут в соответствии с общей формулой (1.7) вид

О xx Ж U x , x +^ 2 U y , y - ^ xx (1 - cos U r ) ;

о yy =X 2 U x , x +x , U y , y - S yy (1 - cos U r ) ;

^ yx = ^ 3 ( U x , y + U y , x ) - S yx (1 - cos U r ).                         (4.5)

Конкретные задачи будем решать при условии, что напряжения постоянны и задаются граничными условиями. Тогда уравнения равновесия (1.6) удовлетворяются.

Распишем систему уравнений (4.1) для микрополей. Для кристалла кубической симметрии она имеет вид

H Ux = - P Lx sin U + k1 Ux,xx + k23 Uyxy + k3 Ux,yy ,

HUy = - PLy sin U + k1 Uy yy + k23 Uxyx + k4 Uy,xx .

Теперь вектор микросмещений лежит в плоскости ( xy ), поэтому эффективный потенциальный барьер несколько иначе выражается через компоненты тензора напряжений

P = p в; p=1-52 N+53 оyx.(4.8)

Здесь N - двумерное давление, а 5 1 , 5 ₂ - материальные коэффициенты,

2N = -(оxx +Оyy);52 = (Sxx + SyyЖ2 +^1); 53 = Syx/^3; .(4.9)

Для поиска решений в аналитическом виде требуются дальнейшие упрощения.

Приближение тонкого слоя

Полагая, что слой простирается в направлении оси 0 Y , вводим естественные допущения

U x << U y ,      l x << L y , U x << Uy      d () /d y <()/dx.              (4.10)

Опустив левую часть в первом уравнении и заменив u на u_y во втором, перепишем систему

0 « k_x U x , xx + k 23 U y , xy ,                                   (4.11)

Ц U y «- PL y sinu y + k_x ^uy , yy + ^k 23 u x , yx + ^k 4 ^uy , xx .                 (4.12)

В первом уравнении также опущено слагаемое u_{x yy} в силу плавности поля вдоль слоя. Оно интегрируется один раз по x , что сводит его к простому уравнению первого порядка

B » k U x , x + k 23 U y , y .                                 (4.13)

Здесь B – константа интегрирования. После его дифференцирования по y можно с его помощью исключить из (4.12) перекрестную производную u_xy x , что дает

Ц u y «- PL y sin u + k 4 u y xx ^{+ k} 5 u y , yy .                       ⁽⁴.1⁴⁾

Правую часть можно упростить, используя (4.11) и приближение L_y * 1 в силу малости компоненты u_x , и записать приближенное уравнение в окончательном виде

Ц u y «^- P Sin u y + k 5 u y yy + k 4 u y xx , ^k 5 = k ^{+ k} 223 / ^k 1 -                ⁽⁴.1⁵⁾

Наряду с (4.14) имеем два уравнения для нахождения полей u_x ( x , y ) и u_y ( x, y ), которые могут быть получены в аналитической замкнутой форме.

5.    Примеры двухкомпонентных задач

Интересуясь статикой, перепишем уравнение (4.15) в соответствующем виде

0 = ^- P sin u y + k ₅ u y yy + k ₄ u y xx , ^k 5 = ^k 1 + k 223 / ^k 1 .                   ⁽5.1)

Рассмотрим три случая возникновения дефектов в поле макроскопических напряжений, учитывая последние в формуле для эффективного потенциального барьера (3.7). Первый случай описывается следующим решением этого уравнения:

tg ( u_y 1 4 ) = acn( xK 1 / H ) / cn( yK ₂ / B ) ,      a ⁴ = v 1² (1 - v 2 ) /v 2 (1 - v 1² ).        (5.2)

Так же, как и в предыдущем случае имеем на самом деле семейство решений с областью произвольных констант интегрирования (см. рис.3).

Дисперсионные соотношения имеют вид

PHг=V2(1 + a2)[(1 + a2)v2 -1]K2/a4 v2; H = H/11, вBг = (1 + a2)[(1 + a2)v2 -1]K22/a2; B = B/12.                   (5.3)

Легко видеть, что, как и в предыдущем случае, здесь точка ветвления решений также достижима. Действительно, правые части дисперсионных уравнений обращаются в нуль при параметрах решения a = 1 или v12 +v2 =1. Но это возможно, когда обращает- ся в нуль бифуркационный параметр в левых частях дисперсионных соотношений, что и означает ветвление решений. Решения вида (5.2) относятся к случаю a > 1 и в > 0 (напряжения согласно (3.9) ниже критических).

В противном случае (упругих деформаций), когда a <  1 и в <  0, напряжения превосходят критические. В этом случае вместо (5.2) получается иное решение, отличающееся, впрочем, лишь сдвигом на половину периода, т.е. ( и ± п ).

Семейство решений (5.2) так же, как и решение (3.18), предсказывает наличие сингулярных дефектов (краевых дислокаций) в нулях эллиптического косинуса у_п = (2 n - 1) B ( n =1,2,3,...) на линиях x m = (2 m - 1) H ( m =1,2,3,...) и разделенных расстояниями 2 H и 2 B . Действительно, в окрестностях этих точек имеем ту же формулу, что и (3.19). В отличие от предыдущего случая знаки дислокаций чередуются в шахматном порядке (рис.10). Проскальзывания же атомов по разные стороны линий скольжения x_m = (2 m - 1) H совершаются, как и в предыдущем случае, на один период решетки u z = 2 п . Такая система зарядов (дислокационных диполей), как известно, устойчива и сама по себе – в отсутствие напряжений.

Распределение плотности энергии дислокаций по спектру D ( v 1 , v ₂), отвечающее решению (3.18) качественно совпадает с распределением, представленным на рисунке 7. Также как и в предыдущем случае, кривая бифуркации ( v 1² + v 2 = 1) уравнения (5.1) разделяет область обратимых и необратимых деформаций. На этой кривой плотность энергии дефектов D ( v 1 , v ₂) логарифмически расходится, образуя «горный хребет». Поэтому оба состояния, разделенные высоким потенциальным барьером, могут сосуществовать как устойчивые. Для завершения задачи о двухкомпонентном поле нужно было бы решить еще линейное уравнение (4.10), доопределив и малую компоненту u_x ( x , у ). Эта задача вполне разрешима, но мы соответствующие громоздкие формулы не приводим.

Рис.10. Картина искажения структуры решетки согласно сингулярному решению (5.1). Диполи краевых дислокаций

Рассмотрим еще одно решение с сингулярными дефектами. Уравнение (5.1) по форме полностью совпадает с уравнением (3.12), лишь в качестве искомой функции фигурирует компонента микрополя u y ( x , y ) и коэффициенты при градиентах другие.

Это дает основания сразу записать его решение в форме (3.18), переменив компоненту микрополя. Получим согласно [10,11]

⁽ u y / ⁴⁾ = ± a

tn( xK 1 / H )

sn( yK 2 / B ) ’

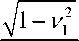
^v 2

(5.4)

Очевидно, что и это решение подчиняется периодическим (вдоль и поперек слоя) условиям, аналогичным (3.17) с периодом 4 В и 2 H соответственно. Разумеется, в них нужно заменить u_z ( x , y ) на u y ( x , y ), что весьма существенно для геометрии деформированной решетки, поскольку вектор микросмещений теперь лежит в плоскости ( xy ). Это значит, что на горизонтальных границах происходит проскальзывание с разрывом, чередующееся периодически. Это уточнение существенно и проявляется в том, что решение (5.4) описывает краевые дислокации. Действительно, здесь справедлива формула для ядра дефекта (3.19), однако в силу того, что теперь вектор микросмещений лежит в плоскости ( xy ) соответствующий дефект является краевой дислокацией с вектором Бюргерса u_y .

Весьма существенно то, что в формуле, аналогичной (3.19), в отличие от (5.4) отсутствуют амплитуда и масштабы фрагментов (расстояния между дислокациями). Следовательно, последняя описывает универсальное ядро единичной дислокации, в то время как (5.4) учитывает и взаимодействие дефектов.

Поскольку знаки зарядов, как и в случае (3.19), чередуются вдоль горизонтальных слоев, но сохраняются вдоль вертикальных, имеем систему малоугловых границ. На рис.11 показано распределение атомов в плоскости ( XY ) в соответствии с полем микросмещений u_z ( x , y ) согласно решению (5.4). Ряды дислокаций и их ядра хорошо видны. Им отвечают междоменные малоугловые границы.

Рис.11. Картина искажения структуры решетки согласно сингулярному решению (5.4). Ряды краевых дислокаций, образующих малоугловые границы

Дисперсионные соотношения полностью повторяют (3.20), лишь бифуркационный параметр раскрывается согласно (4.8). Из них следует и критерий возникновения микроструктуры – зависимость амплитуды от размеров минимального фрагмента и напряжений, в точности повторяющая (3.26).

И, наконец, рассмотрим третий пример, когда сингулярных дефектов не возникает, но образуются периодические наноскопические области неоднородностей. Одно из таких решений уравнения (5.1) имеет вид tg [uy(x,y)]/4 = adn(xK1/H)dn(yK2/B); a4 = 1/(1 -vf)(1 -v22). (5.5)

А также образуются дисперсионные соотношения, которые в точности повторяют (3.33), (3.34), в которых, однако, бифуркационный параметр определяется согласно (4.8).

Некоторые особенности суперструктуры те же, что и для микрополя (3.32). Так, в силу ограниченности функции Якоби dn( * ), правая часть решения (5.5) не обращается в бесконечность, хотя и может быть велика при v ₁ ^ 1 ,v ₂ ^ 1. Это значит, что u y <  2 п , т.е. атомы не перескакивают в соседние ямы, как это происходит при возникновении сингулярностей.

Однако теперь вектор микросмещений лежит в плоскости ( xy ), поэтому геометрия деформированной решетки иная. Соответствующая наноструктура, показанная на рис.12, представляет собой двухмерную периодическую систему нанокристаллов, разделенных широкими границами, где решетка в некоторой степени разупорядочена, но сингулярных дефектов не содержит.

Рис.12.Бездефектная модулированная наноструктура (5.6)

Заметим, что выражение для амплитуды через константы интегрирования в (5.5) несколько иное: оно ограничивает величину амплитуды, которая не может быть меньше 1. По этой причине несколько иным оказывается и критерий возникновения наноструктуры, хотя его вывод аналогичен тому анализу, который был сделан при получении формул (3.37) и (3.38).

Однако в данном случае в=(1 + a2)2 K(vc)/2a3. (5.6)

Эта функция так же, как и (3.37), изображается растущей кривой, уходящей вправо подобно верхней ветви на рис.8. Кривая также выходит из пороговой точки (1,1), а не из точки бифуркации. Поэтому критерий существования микроструктуры (5.5) имеет вид неравенства в> 1; в = HmBm Р/П2. (5.7)

Раскрывая здесь в согласно (4.8), можно прийти к выводу, что критерий и здесь выполняется, безусловно, при любых напряжениях сжатия и при небольших напряжениях растяжения, о чем подробно шла речь в комментариях к формуле (3.37).

В отсутствие внешних напряжений ( в =1) устойчивость масштабов этой наноструктуры, возникающей спонтанно, обеспечивается минимальностью ее энергии D как функции параметров v 1 ,v ₂. Она прямо видна из распределения плотности энергии по спектру пространственных частот, аналогичной представленной на рис.9. Энергия имеет точку наименьшего значения в правом верхнем углу области ( v 1 = 0 , 999 , v ₂ = 0 , 999). К ней и относится структура, показанная на рис.12.

Аналогичным образом рассматривается критическая точка P = 0 или в =0, когда структурная прочность решетки полностью исчерпывается – напряжения достигают пороговых значений a t . Если при этом все же величина комплекса в конечна, то может возникать структура с неопределенно большими масштабами H и B . Действительно, в этом случае формула (5.5) описывает поле микросмещений постоянное в пространстве. Оно возникает за счет жесткого сдвига подрешеток на величину от π до 2π. Этот процесс и требует достижения порогового значения напряжения, о котором шла речь выше.

Заключение

Важной особенностью адекватной теории структурных перестроек должна быть существенная нелинейность процессов, которые могут достигать точек бифуркации структуры и приводить к кардинальным изменениям существующих свойств и появлению новых. К ним нужно отнести и возможность описания самого процесса зарождения дефектов и других повреждений структуры. Построение теории возможно на основе известной модели сложной решетки, элементарная ячейка которой содержит более одного атома. Существующие теории, однако, линейны или, в крайнем случае, учитывают ангармонизмы невысокой степени.

В настоящей теории сильно нелинейные уравнения строятся с учетом принципа внутренней трансляционной симметрии сложной решетки – взаимная трансляция подрешеток на один период (или более) не меняет структуры всей решетки. Это дает возможность сразу ввести периодическую силу взаимодействия соседних атомов в элементарной ячейке, которая отвечает за перестройку локальной топологии решетки. Некоге-рентность деформированных подрешеток является принципиальным, узловым механизмом, который в отличие от классической модели гладкого многообразия не сохраняет локальной топологии среды в процессе деформирования.

В результате удается проследить ряд интересных механизмов структурных превращений на уровне точных решений нелинейных уравнений. Впервые удается выявить такие нетривиальные эффекты, как переключение межатомных связей за счет понижения потенциальных барьеров под влиянием внешних напряжений. В результате предсказываются образование дефектов решетки в изначально идеальной структуре, ее фрагментация с разрывными границами, потеря устойчивости однородных деформаций за порогом интенсивного воздействия на тело, возникновение полос скольжения и двойниковых включений, неупругие бездиффузионные деформации, нарушение дальнего и ближнего порядка, реконструкция поверхности. Интересно, что в условиях сложнонапряженного состояния наряду с разупрочнением возможны и обратные эффекты – упрочнение решетки. Получены критерии переходов в форме разветвляющихся зависимостей амплитуды микроскопического поля от напряжений и размеров доменов вновь образующейся микроструктуры.

Макроскопические напряжения могут рассматриваться, в частности, как внешнее поле и единственная причина, приводящая к бифуркационному переходу от однородных к неоднородным деформациям при больших (закритических) напряжениях. Однако и в их отсутствие возможна спонтанная перестройка структуры, сопровождающаяся образованием и макроскопических деформаций. Подобные эффекты наблюдаются в сегнето-эластических кристаллах. Разумеется, полная термодинамическая теория суперструктуры дефектов должна была бы включать и анализ её устойчивости в поле температур.

Отвлекаясь от деталей можно утверждать, что феноменологическая теория двойного континуума находит в принципе свое обоснование в пределах конкретной модели сложной решетки. Существенно, что при этом сохраняется важный принцип диффеоморфизма модели. Принципиальное отличие от классической теории континуума состоит в том, что нужно вводить двойное преобразование для каждого из подконтинуумов. При этом, если в естественном начальном состоянии отсчета оба подконтинуума могут быть конгруэнтны (совмещаются жестким сдвигом в пространстве на структурный вектор u_o - const ), то в результате деформирования это свойство утрачивается. В результате возникает изменение не только метрики, но и локальной топологии, описываемое переменным полем вектора u_i .

И, наконец, отметим еще одно принципиальное обстоятельство. Мы использовали новый принцип внутренней трансляционной симметрии, который позволил построить нелинейную теорию на основе трансляционно-инвариантного функционала. Естественно было бы учесть и относительную точечную симметрию сложной решетки (поворот одной подрешетки относительно другой), введя инвариантность энергии к относительным поворотам подрешеток, наряду конечно с общей симметрией сложной решетки как единого объекта.

В динамике соответствующие бифуркации приводят к возникновению ударных волн скачка деформаций и их скоростей [5,6].