Сильнокоррелированная спиновая жидкость в гербертсмитите

Поиск материалов, содержащих ферми-спи-ноны-частицы со спином 1 /2 и нулевым зарядом, является важной задачей физики конденсированного состояния вещества [1]. Экспериментальное изучение отдельных кристаллов гербертсмитита ZnCu3 (OH)6Cl2 не обнаружило ни дальнего магнитного порядка, ни структур типа спинового льда. Это позволяет надеяться на то, что ZnCu3 (OH)6Cl2 является перспективной системой для изучения квантовой спиновой жидкости (КСЖ) [2–11]. Теоретическое изучении КСЖ началось с основополагающей статьи Андерсена [12], которая инициировала жаркие дискуссии в научном сообществе. КСЖ может рассматриваться как экзотическое квантовое состояние вещества, состоящего из гипотетических частиц — беззарядовых ферми-спинонов, имеющих спин 1 /2 и способных к течению, как обычная жидкость. Существует теоретическое мнение, что основное состояние КСЖ не должно иметь магнитного упорядочения как в случае спиновых жидкостей со щелью, так и без нее [1]. Экспериментальное исследование КСЖ ограничено нехваткой реальных веществ, в которых они могут существовать. Точнее, до недавнего времени не было найдено ни одного надежного модельного вещества с КСЖ, хотя можно было назвать несколько возможных кандидатов в их число. Таким образом, поиск материалов с явной реализацией КСЖ является принципиальной задачей в современной физике конденсированного состояния вещества. До настоящего времени гербертсми- тит ZnCu3 (OH)6Cl2 считался Гайзенберговским антиферромагнетиком [2] на совершенной кагоме решетке. Однако недавние экспериментальные исследова-яния выявили ряд необычных свойств этого соединения [3–7]. В ZnCu3 (OH)6Cl2 ионы Cu2+ , имеющие спин S = 1/2, образуют плоские слои из треугольных кагоме решеток, которые разделены немагнитными промежуточными слоями из атомов Zn и Cl. Слои из ионов Cu2+ могут рассматриваться как двухмерные (2D) подсистемы с пренебрежимо малым магнитным взаимодействием в перпендикулярном к их поверхности направлении. Специальные эксперименты [3, 7] показали, что в них нет ни дальнего магнитного порядка, ни замораживания типа спинового стекла вплоть до температуры 50mK, что делает ZnCu3(OH)6Cl2 лучшим кандидатом на вещество, в котором реализуется КСЖ. Фрустрации в элементарных ячейках кагоме решеток гербертсмити-та приводят к бездисперсионным, топологически защищенным ветвям в одночастичном спектре с нулевой энергией возбуждения, известным как ”плос-кая зона” [13, 14]. В этом случае спиновую систему ZnCu3 (OH)6Cl2 , состоящую из беззарядовых подвижных фермионов со спином S = 1/2, занимающих соответствующую Ферми сферу с ферми-импульсом pF , можно считать сильнокоррелированной квантовой спиновой жидкостью (СККСЖ). Для ее описания может быть применена концепция ферми конденсатного квантового фазового перехода (ФККФП) [16]. Поскольку мы имеем дело с 3D соединением ZnCu3 (OH)6Cl2, а не с идеальной 2D кагоме решеткой, мы должны понимать, что реальные магнитные взаимодействия в веществе могут сдвигать состояние СККСЖ относительно ФККФП в соответствии с фазовой Т-В диаграммой, помещая его либо до, либо после квантовой критической точки (ККТ). Поэтому реальное состояние СККСЖ может быть установлено только путем анализа экспериментальных данных. С одной стороны, считается общепринятым, что спиновая с S = 1/2 модель на кагоме решетке может рассматриваться как безщелевая спиновая жидкость [3–11]. С другой стороны, недавние довольно точные вычисления утверждают, что эта жидкость полностью гаппирована (см. [15] и содержащиеся в ней ссылки). Таким образом, существует настоятельная необходимость проверить, какого типа КСЖ формируется в гербертсмитите и определить ее низкотемпературные термодинамические и релаксационные свойства.

Для того, чтобы однозначно идентифицировать соединение, имеющее экзотическую СККСЖ, находящуюся в критической точке ФККФП [16, 17], мы должны проанализировать не один, а целый набор экспериментов. При очень низких температурах и при наложенных магнитных полях можно ожидать, что возможное вещество с КСЖ будет демонстрировать Ландау Ферми жидкостное (ЛФЖ) поведение его физических характеристик, таких как магнитная удельная теплоемкость и восприимчивость, частота спин-решеточной релаксации и коэффициенты теплопроводности. В то же время при повышении температуры появляется не Ферми жидкостной (НФЖ) режим, отделенный от ЛФЖ режима переход- ной (или кроссоверной) областью. Другими словами, при изменении температуры вещество-кандидат должно демонстрировать ЛФЖ, НФЖ и переходный режимы аналогичные тем, что наблюдаются у металлов с тяжелыми фермионами (ТФ) и 2D 3He [16–19]. Это означает, что СККСЖ играет роль ТФ жидкости, помещенной в изоляторную среду. В то время как электрон, которому принадлежит спин, локализован, сам спин мигрирует. Такое поведение получило название спин-зарядовое разделение, недавно наблюдаемое в 1D системах взаимодействующих нелока-лизованных электронов [20]. В нашем случае заряды полностью локализованы, в то время как спины перемещаются в пределах топологически защищенной зоны. В результате мы имеем поразительную картину: новые частицы управляют свойствами системы при низких температурах и это не те частицы, которые присутствуют в гамильтониане, описывающем систему.

2.    Магнитная восприимчивость и удельная теплоемкость СККСЖ

Начнем с анализа магнитной восприимчивости χ ( T ) ZnCu 3 (OH) 6 Cl 2 , приведенной на панели А (рис. 1). Она демонстрирует необычное поведение [5]: для B ≥ 3 T χ ( T ) имеет максимум χ max ( T ) при некоторой температуре T max ( B ) .

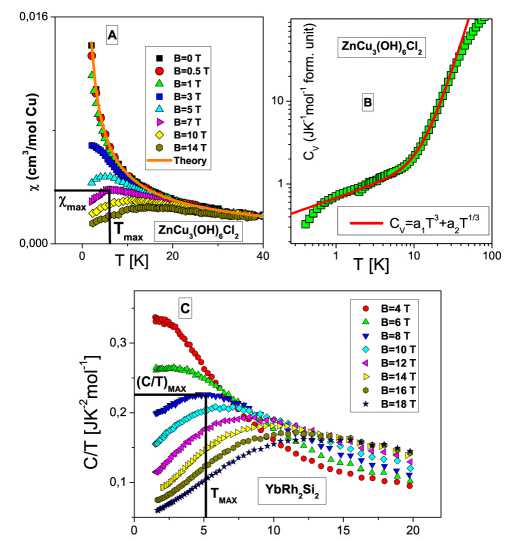
Рис. 1. Панель А: Температурная зависимость магнитной восприимчивости х Для различных магнитных полей [5], представленных на рисунке. Величины хmax и Tmax при B = 7T приведены там же. Наши вычисления при B = 0 обозначены сплошной кривой и соответствуют х(T) ^ T-“ с а = 2/3. Панель В: Теплоемкость, измеренная в ZnCu3(OH)6Cl2 при B = 0 [4], обозначена квадратами. Сплошная линия соответствует нашей теоретической аппроксимации, с использованием функции C = a 1 T3 + a2 T1 / 3, где a 1 и a2 — подгоночные параметры (см. уравнение (9)). Панель С: Температурная зависимость электрон- ной удельной теплоемкости C/T для YbRh2Si2 для различных магнитных полей [21], представленных на рисунке. Там же приведены значения (C/T)max и Tmax При B = 8T.

Величина максимума χ max ( T ) уменьшается с ростом магнитного поля B , в то время как T max ( B ) сдвигается в сторону больших температур T , достигая 15 K при B = 14 T . Из панели А (рис. 1) видно, что χ ( T ) к т ^а с а = 2 / 3 . Вычисленный нами показатель совпадает с экспериментальным значением а = 2 / 3 ~ 0 . 66 [5]. Наблюдаемое поведение х сильно напоминает ее поведение в металлах с ТФ и очень близко результатам вычислений в теории ФККФП [16, 17]. Теплоемкость C , связанная со спиновой системой Cu , в исследованной области низких температур 106 < T <  400 mK демонстрирует линейную зависимость от температуры, C к т . Как видно из панели В (рис. 1), для температур от нескольких Кельвинов и выше теплоемкость C ( т ) к т 3 , что соответствует преимущественному вкладу в теплоемкость колебаний решетки. При низких температурах, т <  1 K , сильная зависимость теплоемкости C от магнитного поля позволяет заключить, что она формируется в основном вкладом теплоемкости C mag КСЖ, C mag = C - a i т 3 , поскольку вклад решетки не зависит от поля B [3–5]. Иллюстрацией сказанного может служить рис. 2. Поскольку в ЛФЖ области при к в т . м в в , C ( b,t ) к м * т к в ^{- 2} / ³ т , то, как будет показано позднее, поле B полностью определяет поведение M ^∗ ( B ) в соответствии с уравнением (3). Как видно из рис. 2, наши вычисления хорошо согласуются с результатами измерений, когда система демонстрирует ЛФЖ поведение. Действительно, если при т = 1 K система ведет себя как ЛФЖ для в >  2 т , то при T = 0 . 5 K ЛФЖ поведение наблюдается при значительно более слабых полях, примерно в >  1 т .

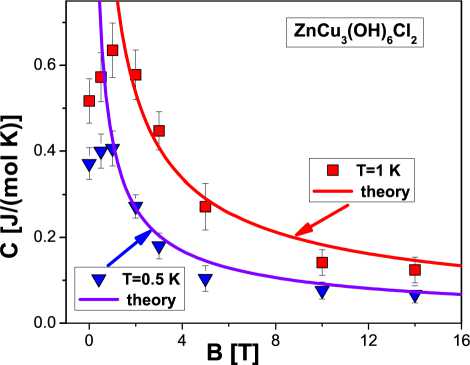
Рис. 2. Удельные теплоемкости C ( В,т ) как функции магнитного поля B , измеренные в ZnCu ₃ (OH) ₆ Cl ₂ при двух различных температурах т [3], значения которых приведены на рисунке, обозначены треугольниками и квадратами. Наши вычисления представлены сплошными линиями, соответствующими ЛФЖ поведению C ( В,т ) = a 1 B ^{- 2} / ³ т (см. уравнение (3) ), где a 1 — подгоночный параметр.

Описанное выше поведение χ (рис. 1), панель A сильно напоминает аналогичные характеристики металлов с ТФ, наблюдаемые при измерениях C/T в YbRh2Si2 , представленных на панели C (рис. 1). Это совпадение станет очевидным, если мы вспомним, что для ТФ жидкости х к C/т [16]. Из панели С (рис. 1) видно, что электронная удельная теплоемкость YbRh2Si2 [21] также сильно зависит от наложенного магнитного поля и, как мы увидим далее, эта теплоемкость и теплоемкость Cmag для ZnCu3(OH)6Cl2 демонстрируют одинаковое поведение.

3.    Влияние температуры и магнитного поля на СККСЖ

Для теоретического изучения низкотемпературных термодинамических, релаксационных и скейлинговых свойств гербертсмитита мы использовали модель однородной ТФ жидкости [16]. Эта модель позволяет избежать усложнений, связанных с анизотропией кристаллической структуры вещества. В нашем случае определенная ранее СККСЖ состоит из беззарядовых фермионов (спинонов) со спином S = 1 / 2 , занимающих соответствующую Ферми сферу с ферми-импульсом p _F . Энергия основного состояния E ( n ) рассматриваемой системы задается функционалом Ландау, зависящим от функции распределения квазичастиц n σ ( p ) , где p импульс, а σ спиновый индекс. Эффективная масса M ^∗ определяется уравнением Ландау [16, 22]

1       1    1 ∑ ^∫ p _F p 1

M ^∗ ( T,B ) ⁼ M ^{∗ +} p ²        p F

F σ 1

∂δn σ 1 ( p 1 , T, B ) d p 1

X F^ 1 ( p F , ^p 1)------ dp 1 ------(2 П ) 3 •    ⁽¹⁾

Здесь мы переписали функцию распределения квазичастиц в виде n _a ( p , T, B ) = n _a ( p ,т = 0 , B = 0) + Sn _a ( p , T, B ) . Амплитуда Ландау F полностью определяется тем фактом, что система находится в ККТ ФККФП [16, 23–25]. Решение уравнения (1) подробно описано в [25]. Основная роль амплитуды Ландау состоит в том, что она помещает систему в точку ФККФП, где поверхность Ферми изменяет свою топологию так, что эффективная масса квазичастиц начинает зависеть от температуры и магнитного поля. В этой точке слагаемое 1 /м * в уравнении (1) исчезает. Оно становится однородным и может быть решено аналитически [16, 23]. При конечных температурах и B = 0 эффективная масса, сильно зависящая от T , демонстрирует НФЖ поведение, следующее из уравнения (1)

M * ( T ) ~ a _T T ^{- 2} / ³ .                (2)

При конечных температурах T , наложение магнитного поля B переводит систему в область справедливости ЛФЖ теории, что также вытекает из уравнения (1)

M * ( B ) ~ a _B B ^{- 2} / ³ .               (3)

Из уравнений (2) и (3) следует, что эффективная масса расходится в точке ФККФП. При конечных B и T вблизи ФККФП решение уравнения (1) для M* (B,T) может быть аппроксимировано простой универсальной интерполяционной функцией. Эта интерполяция хорошо работает от режима ЛФЖ, задаваемого уравнением (3), до НФЖ режима, задаваемого уравне- нием (2) [16, 23]. В случае сильно коррелированных ферми-систем, таких как ТФ металлы и 2D 3He, их термодинамические и релаксационные свойства определяются эффективной массой M∗, а именно, х к (с/т) к V1 /т1 т к м*, где 1 /т1 т к х2 есть частота спин решеточной релаксации [16]. Для изучения универсальных скейлинговых свойств сильнокоррелированных ферми-систем удобно определить нормированную эффективную массу MN∗ и нормированную температуру TN путем деления эффективной массы M∗ и температуры T на ее максимальное значение MM∗ и температуру TM , при этом значении, соответственно. Поведение MN = M*/MM как функции у = т/тм, представленное на вставке в рис. 3, не зависит от специфических свойств конкретной сильнокоррелированной ферми-системы, в то время как MM∗ и TM полностью определяются свойствами этой системы [16]. В результате мы получаем [16]

Control parameter, magnetic field В

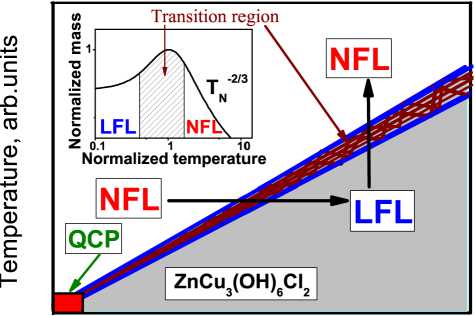
Рис. 3. Схематическая Т-В фазовая диаграмма гер-бертсмитита 7пСиз(ОН)бСЬ. Квадрат в начале координат, показанный стрелкой, обозначает ККТ, около которой находится КСЖ. Вертикальные и горизонтальные стрелки показывают ЛФЖ-НФЖ и НФЖ-ЛФЖ переходы при фиксированных B и т соответственно. При фиксированном т увеличение B переводит систему вдоль горизонтальной стрелки из НФЖ режима в ЛФЖ. С другой стороны, при постоянном B и увеличивающейся температуре система смещается вдоль вертикальной стрелки из ЛФЖ режима в НФЖ. Вставка представляет поведение нормированной эффективной массы MNN как функции нормированной температуры TN в соответствии с уравнением (5). Видно, что температуры 7 v ~ 1 обозначают переходную область между ЛФЖ режимом с почти постоянной эффективной массой и НФЖ режимом, демонстрирующим т-2/3 зависимость эффективной массы от температуры. Из уравнения (5) видно, что ширина переходной области Tw к т к B. Переходная область, когда MNN достигает максимума при т/тmax = 1, показана стрелками и заштрихованной областью на ос новном рисунке и вставке в него.

XN = (Cmag /т) N = ( V1 /т1 т) N = M*, (4) где XN, (с/т) N и (V1 /т1 т)N нормированные значения х, C/т и V1 /т1 т, соответственно. В качестве типичного примера значения χmax и Tmax , использованные для нормировки восприимчивости, приведе- ны на рис. 1, панели A и C. Отметим, что наши вычисления MN∗ , основанные на уравнении (1) не содержат каких-либо подгоночных параметров. Нормированная эффективная масса MN = M*/м*м как функция нормированной температуры y = TN = т/тм имеет вид mN (у) * c 0 .1+ c1 yL.            (5)

1 + c 2 У ⁸ / ³

Здесь c0 = (1 + c2)/(1 + ci), ci и c2 подгоночные параметры, аппроксимирующие амплитуду Ландау. Поскольку магнитное поле B входит в выражение (1) только в виде отношения BµB/T , получаем Tmax ∝ BµB [16, 23]. Таким образом, для конечных магнитных полей переменная y приобретает вид y = т/тм к т/цвB.            (6)

Мы будем использовать уравнение (5), чтобы в упрощенной форме продемонстрировать наши вычисления, основанные на уравнении (1). Переменные B и T входят в уравнение (1) симметрично, поэтому уравнение (5) определяет M∗ как функцию B при фиксированном T [16]. Из уравнений (3), (5) и (1) прямо следует, что х(квт/цвB) т2/3 — х(т, B) т0•66 к у2/3MN (у). (7)

Поскольку намагниченность M ( т, B ) = J х ( т, b ) db , следовательно

M ( т,В ) т - ¹ / ³ — M ( т,В ) т ^{- 0} • ³⁴         (8)

и зависит только от одной переменной y . Уравнения (7) и (8) подтверждают скейлинговые свойства как χT ^{0 . 66} , таки MT ^{- 0 . 34} , экспериментально установленные в [5].

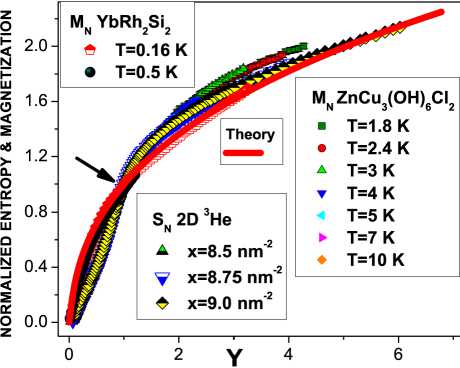
Рис. 4. Нормированная намагниченность M _N ( у ) , полученная из измерений в ZnCu ₃ (OH) ₆ Cl ₂ [5] и в YbRh 2 Si 2 [27] при различных температурах, значения которых указаны на рисунке. Обозначенный стрелкой излом ясно виден при у — 1 . Нормированная энтропия S _N ( у ) получена из измерений в 2 D ³ He [26] при различных плотностях х , значения которых приведены на рисунке. Сплошной линией изображены результаты наших вычислений нормированной намагниченности.

Нормированная намагниченность MN(у) = M(B/Bk)/M(Bk) , полученная из измерений намагниченности M(B) [5], изображена на рис. 4 в ви- де геометрических фигур. Вычисленная нами MN(у) изображена на рис. 4 в виде сплошной линии. Здесь Tk – температура, при которой намагниченность демонстрирует излом, когда система входит в переходную область, изображенную на рис. 3 [16]. Нормированная энтропия SN(у) = S(T/Tinf)/S(Tinf) получена из измерений энтропии S в 2D 3He [26]. Здесь Tinf – температура, при которой система входит в переходную область, а S обладает точкой перегиба, ясно видимой на экспериментальных данных (см. вспомогательные онлайн материалы для [26], рис. S8, A). Как видно из уравнения (5) и из вставки в рис. 3, при у < 1, SN = MN х у, а при у > 1, SN = MN к у1 /3. Такое поведение порождает излом и заставляет участки линии с разными наклонами слиться в одну кривую, описываемую переменной y [16]. Наши вычисления находятся в хорошем согласии с измерениями.

4.    Фазовая диаграмма СККСЖ

Рассмотрим схематическую Т-В фазовую диаграмму 7пСп з (ОН) б С1 2 . Она представлена на рис. 3. При T = 0 и B = 0 система находится вблизи ККТ ФККФП без дополнительной настройки. Фактически она находится перед ККТ ФККФП со стороны неупорядоченного состояния, поскольку С ( T ) демонстрирует ЛФЖ поведение, характеризуемое линейной зависимостью от T при низких температурах [3].

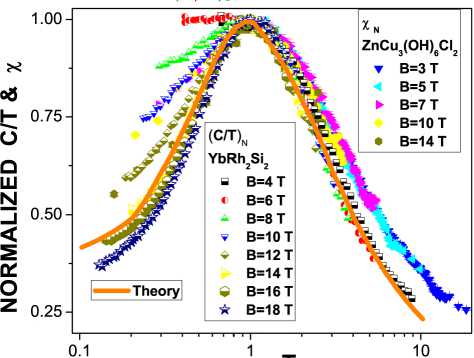
Магнитное поле B и температура T играют роль управляющих параметров, перемещая систему из НФЖ в ЛФЖ область, как показано вертикальной и горизонтальной стрелками. Из рис. 5 следует, что в соответствии с уравнением (4) поведение χ _N совпадает с поведением ( C/T ) N для YbRh ₂ Si ₂ .

N

Рис. 5. Экспериментальные данные по измерению Xn [5], (C/T)n = MN [21] и наши вычисления MN при постоянном сильном магнитном поле (сильное — означает то, что оно полностью поляризует спины квазичастиц) показаны фигурами различной формы и сплошной линией соответственно. Ясно видно, что данные, относящиеся как к 7пСщ(ОН)бС12, так и к YbRh2Si2, слились в одну кривую, демонстрируя скейлинговые свойства. В соответствии с фазовой диаграммой, представленной на рис. 3, при увеличении температуры (до у ~ 1 ) ЛФЖ режим преобразуется в переходный, который затем становится НФЖ режимом. Из этого следует, что спиновая жидкость гербертсмитита находится вблизи ККТ и ведет себя аналогично ТФ жидкости YbRh2Si2 в сильных маг нитных полях [25].

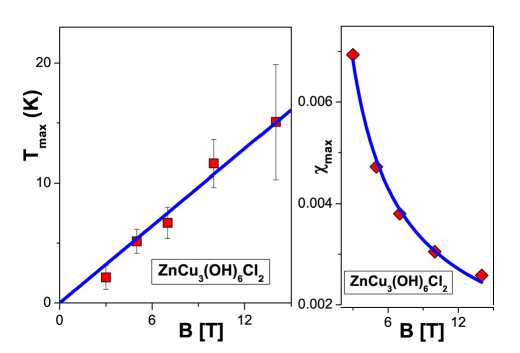
Рис. 6. Левая панель: Температура T _max ( B ) , при которой x (см. рис. 1, панель A) достигает максимума. Сплошная линия представляет функцию T max к аВ , а подгоночный параметр (см. уравнение (6) ). Правая панель: Максимальное значение х max магнитной восприимчивости х ( T ) как функция магнитного поля B (см. рис. 1, панель A). Сплошная линия представляет аппроксимацию этих точек функцией X max ( B ) = dB - ² / ³ (см. уравнение (3) ), d подгоночный параметр.

Рисунок 6: правая и левая панели соответственно демонстрируют, что уравнения (6) и (3) находятся в хорошем согласии с результатами экспериментов.

5.    Скейлинговые свойства термодинамических функций СККСЖ

В соответствии с уравнением (4), в случае СККСЖ поведение нормированной удельной теплоемкости, деленной на T , ( C mag /T ) N , должно совпадать с поведением χ _N . Для того, чтобы выделить вклад C mag , мы аппроксимировали общую теплоемкость С ( T ) при T >  2 K функцией

С ( T )= а 1 T ³ + а 2 T ¹ / ³ , (9)

где первое слагаемое, пропорциональное T ³ , отвечает за вклад решетки (фононов), а второе слагаемое определяется вкладом СККСЖ, когда она демонстрирует НФЖ поведение в соответствии с уравнением (2). Из рис. 1 (панель B), видно, что такая аппроксимация справедлива для широкого интервала изменения температуры. Отметим, что величина a 1 , почти не зависимая от a 2 , позволила нам добиться значительно более точной аппроксимации для C . Полученная удельная теплоемкость С тад IT = ( С - a i T 3 ) /T представлена на левой панели (рис. 7), в то время как на правой панели В приведена температура максимума теплоемкости как функция магнитного поля B . Можно заметить, что C mag /T ∝ M ^∗ ведет себя как χ ∝ M ^∗ , приведенная на рис. 1 (панель A).

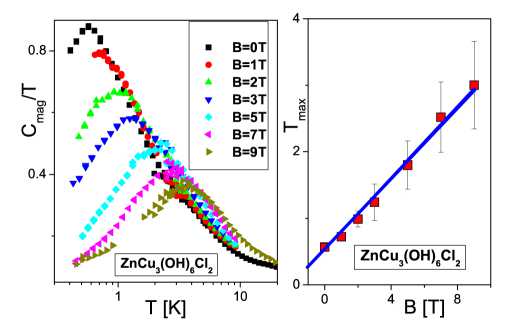
Рис. 7. Левая панель: Удельная теплоемкость C mag /Т СККСЖ, полученная с использованием уравнения (9) из измерений теплоемкости C ( B ) в ZnCu 3 (OH) 6 C1 2 при различных магнитных полях, значения которых приведены на вставке в рисунок [4]. Правая панель: Температура Т max ( B ) , при которых достигаются максимумы C mag /Т (см. левую панель) в зависимости от напряженности наложенного магнитного поля B . Сплошная линия представляет функцию Т max к B (см. уравнение (6) ).

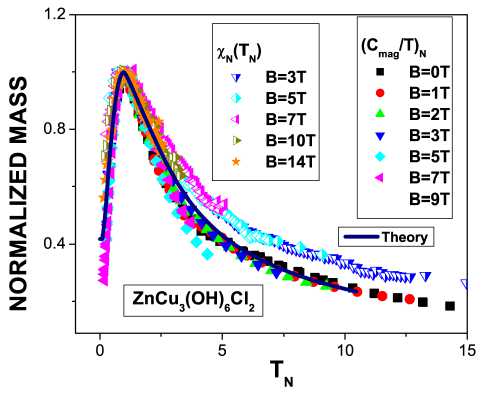
Рис. 8. Нормированная восприимчивость x N = x/x max = M N и нормированная теплоемкость ( C mag /Т ) N = M N как эффективная масса КСЖ в зависимости от нормированной температуры T _N для различных магнитных полей, указанных на рисунке. x N получена из измерений магнитной восприимчивости x для различных магнитных полей B [5], приведенной на панели А (рис. 1). Нормированная теплоемкость получена из данных, представленных на рис. 7, левая панель. Наши вычисления изображены сплошной линией, демонстрирующей скейлин-говое поведение M N .

На рисунках 8 и 9 представлены нормированные (Cmag /T)N и χN. Из этих рисунков видно, что результаты, полученные для различных образцов и в различных экспериментах [3, 4], демонстрируют одинаковые свойства. Как видно из рисунков 5, 8 и 9 и в соответствии с уравнением (4), (Cmag /T )N ≃ χN демонстрирует такое же скейлинговое поведение, как и (C/T)N, измеренная в металле сТФ, YbRh2 Si2. Таким образом, скейлинговое поведение термодинамических функций гербертсмитита является характерной особенностью этого соединения и никак не определяется магнитными примесями в нем. Это наблюдение позволяет исключить, что дополнительные спины Cu> вне кагоме плоскостей, действующие как парамагнитные примеси, могут привести к расходимости магнитной восприимчивости при низких температурах и разрушить скейлинговое поведение.

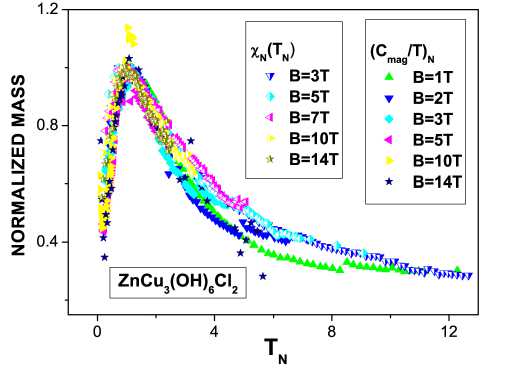
Рис. 9. Нормированная восприимчивость x N и нормированная теплоемкость ( C mag /Т ) n , выраженные через эффективную массу квазичастиц СККСЖ как функции нормированной температуры T N для различных значений магнитного поля, указанных на рисунке. x N и ( C _mag /Т ) N получены из работ [5] и [3], соответственно.

6.    Частота спин-решеточной релаксации СККСЖ

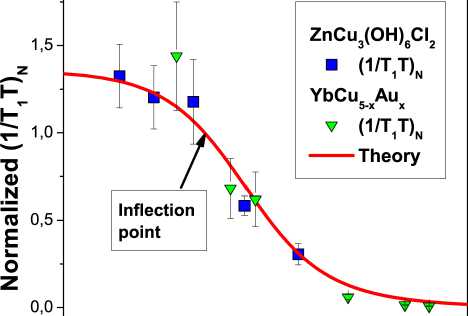
На рис. 10 представлены нормированные частоты спин-решеточной релаксации (1 /T 1 T ) _N как функции нормированного магнитного поля B _N при фиксированных температурах.

i                ' ......10

Normalized magnetic field BN

Рис. 10. Релаксационные свойства гербертсмитита при сравнении с аналогичными характеристиками металлов с ТФ и 2 D ³ He . Нормированная частота спин-решеточной релаксации (1 /Т 1 Т ) n при фиксированной температуре как функция магнитного поля. Квадратами обозначены данные для (1 /Т 1 Т ) n , полученные из измерений в ZnCu 3 (OH) 6 Cb [28], а треугольниками — аналогичные данные, полученные из измерений в YbCu 5 _ _x Au _x с x = 0 . 4 [29]. Точка переги-

áà, èñïîëüçîâàííàÿ äëÿ íîðìèðîâêè, óêàçàíà ñòðåë-êîé. Íàøè âû÷èñëåíèÿ ïðåäñòàâëåíû íåïðåðûâíîé ёи^ией, изображающей фy^кцию ( M N ( B )) 2 .

Из рис. 10 следует, что с ростом магнитного поля B величина 1 /т 1 т монотонно убывает, проходя через точку перегиба при некотором значении магнитного поля B = B inf , показанного стрелкой. Для того, чтобы выявить скейлинговый характер частоты релаксации, необходимо нормировать как 1 /т 1 т , так и магнитное поле. А именно, необходимо нормировать 1 /т 1 т на ее значение в точке перегиба, а магнитное поле — на B inf , B N = B/B inf . Из уравнения (4) следует, что (1 /т 1 т ) N = ( M N ) ² и можно ожидать, что различные сильнокоррелированные ферми-системы, находящиеся вблизи ФККФП, будут демонстрировать аналогичное поведение нормированной спин-решеточноой частоты релаксации [16]. Из рис. 10 видно, что как металл с ТФ, YbCu 5 _ x Au x , так и гербертсмитит, ZnCu 3 (OH) 6 Cl 2 демонстрируют одинаковое поведение нормированной частоты спин-ре-шеточной релаксации. Из рис. 10 также видно, что при B < B inf (или B N <  1 ) нормированная частота релаксации (1 /т 1 т ) N слабо зависит от магнитного поля, в то время как при более высоких полях (1 /т 1 т ) N изменяется в соответствии с уравнением (3), (1 /т 1 т ) _N = ( M N ) ² к B - ⁴ / 3 . Таким образом, можно заключить, что наложение магнитного поля B приводит к переходу из НФЖ в ЛФЖ режим и к существенному уменьшению частоты релаксации СККСЖ гербертсмитита. Как было отмечено ранее, СККСЖ играет роль ТФ жидкости, помещенной в диэлектрическое окружение. Можно предположить, что СКК-СЖ в гербертсмитите ведет себя так же, как электронная жидкость в ТФ металлах, как если бы заряд электронов был равен нулю. В этом случае термическое сопротивление ( w = ът/к ), w = w 0 + A w т 2 , СККСЖ ведет себя как электрическое сопротивление р = р 0 + А р т ² электронной жидкости, и следовательно, A w представляет вклад спинон-спинон-ного рассеяния в транспорт тепла. Это аналогично вкладу A ρ в транспорт заряда за счет электрон-элек-тронного рассеяния. Здесь L – число Лоренца, κ – термическая проводимость СККСЖ, ρ 0 и w 0 – остаточные электро- и термосопротивления электронной жидкости и СККСЖ, соответственно. Коэффициенты A w ~ А р к ( M * ) ² [30]. Можно предсказать, что коэффициент A w термического сопротивления СККСЖ при наложении на систему магнитного поля при фиксированной температуре будет вести себя как частота спин-решеточной релаксации, показанная на рис. 10, A w ( B ) к 1 /т 1 т ( B ) к ( M * ( B )) ² , а в ЛФЖ режиме при постоянном магнитном поле термическая проводимость является линейной функцией температуры, κ ∝ T .

7.    Выводы

В работе были определены термодинамические и релаксационные свойства гербертсмитита. Вычисления выявили фундаментальные свойства СККСЖ, являющейся сильнокоррелированной ферми-системой и находящейся вблизи ФККФП. Результаты хорошо согласуются с экспериментальными данными, что позволяет считать поведение СККСЖ схожим с поведением ТФ металлов. Ключевой особенностью КСЖ является спин-зарядовое разделение и формирование СККСЖ, состоящей из подвижных тяжелых спинонов. Гербертсмитит является привлекательным минералом для изучения. В нем новые частицы-спиноны, не существующие в свободном состоянии, полностью замещают исходные частицы-электроны и определяют его низкотемпературные свойства. С целью дальнейшего прояснения физических свойств гербертсмитита полезно выполнить подробное экспериментальное изучение транспорта тепла. Интересно выяснить условия, при которых спиновая жидкость переходит в сверхтекучее состояние.

Мы благодарны В.А. Ходелю за ценные обсуждения, а также А. Харрисону и М.А. де Врие за их помощь в трактовке, полученных ими экспериментальных данных [4]. Эта работа была поддержана U.S. DOE, Division of Chemical Sciences, Office of Basic Energy Sciences, Office of Energy Research, AFOSR и РФФИ # 12-02-00017.