Силовой расчет цепной передачи с зубчатой цепью и эвольвентными звездочками

УДК 621.855

Введение . Цепные передачи с зубчатой цепью недостаточно исследованы. Их выпуск ограничен, однако они все шире используются в производстве. Например, такими передачами комплектуют приводные механизмы в машинах, в прецизионных станках и другой технике. В представленной работе исследуется силовой анализ и расчет тяговой способности передач с зубчатой цепью и эвольвентными звездочками.

Тяговая способность определяет работоспособность эвольвентной зубчатой цепной передачи, которая зависит от ряда факторов 1 . В их числе:

— геометрия передачи,

• —    предельное контактное напряжение наиболее слабого элемента пары «пластина цепи — зуб звездочки»,

• —    коэффициент сцепления зубчатой цепи с зубьями звездочки,

• —    наличие пробуксовки зубчатой цепи по зубьям звездочки,

• —    допустимое удельное давление внутри шарнира, — ударная стойкость элементов зубчатой цепи 2 [1–3].

  Машиностроение и машиноведение

  
  

Материалы и методы. Коэффициент сцепления — это один из основных факторов тяговой способности цепной передачи, оснащенной зубчатой цепью. Во время работы такой передачи возникает зацепление и действуют силы, которые перемещают пластины цепи по рабочему и затылочному профилям зубьев звездочки [4–7]. На дуге обхвата эвольвентной звездочки зубчатой цепью любые ее звенья (звено i , i + 1, i + 2 и т. д.) испытывают:

• —    силу трения N i f цепи о зуб звездочки,

• —    растягивающую силу Q i соседних звеньев,

• —    силу нормального давления N i профиля зуба звездочки (рис. 1).

• 1    Курапов Г. В. Исследование работоспособности цепной передачи с зубчатой цепью и эвольвентными звездочками : дис. канд. тех. наук. Краснодар, 2019. 173 с.

• 2    Семенов В. С. Обеспечение работоспособности роликовых цепных передач на стадии их эксплуатации // Сб. мат - лов всерос. науч. - практ. конф. аспирантов, докторантов и молодых ученых. Майкоп, 2017. С. 121 – 125.

  

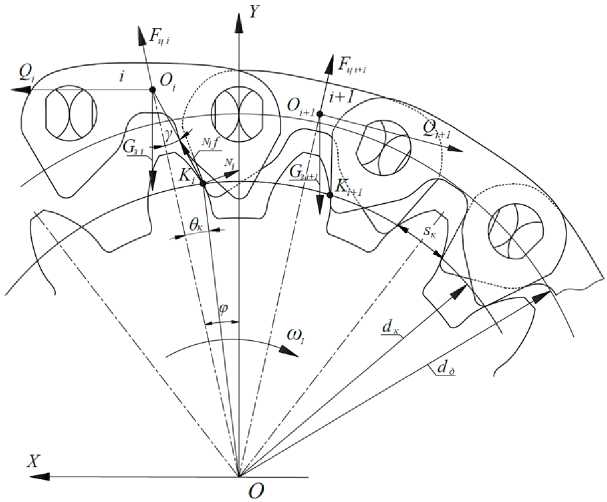
  Рис. 1. Схема расположения пластин в зацеплении с зубьями эвольвентной звездочки

  
  

В литературе коэффициент сцепления рассчитывается отношением растягивающих сил Q i и Q i ₊₁ в смежных звеньях цепи:

Q i

.

Q + 1

Данный коэффициент непостоянен, поэтому пластины зубчатой цепи перемещаются по профилям зубьев звездочек на всей дуге обхвата. На рис. 2 представлено зацепление первого пакета пластин (звена) цепи с зубом звездочки.

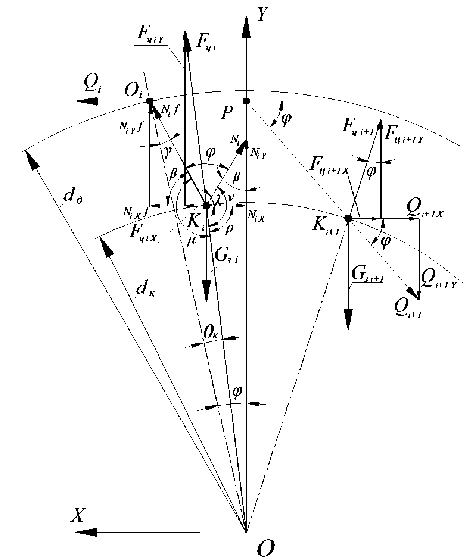
Рис. 2. Схема сил, действующих в зацеплении пластины зубчатой цепи со звездочкой

На эвольвентный профиль зуба звездочки действуют перечисленные ниже факторы [8-14].

• 1.    Сила трения Nif, препятствующая перемещению пакета пластин к вершине зуба звездочки. Здесь f— коэффициент трения.

• 2.    Вес пакета пластин цепи G з = m , g . Здесь g — ускорение свободного падения, m i — масса звена цепи

• 3.    Сила нормального давления N i профиля зуба звездочки, сосредоточенная в месте зацепления K i .

• 4.    Растягивающие силы Q i и Q i +1 смежных звеньев зубчатой цепи.

• 5.    Центробежная сила, учитывающая массу звена зубчатой цепи Е ц = ~~- Здесь _ю — угловая скорость вращения звездочки. R — радиус центральной части звена (представлена как окружность, меняющая положение при вращении звездочки) на эвольвентном профиле зуба звездочки.

в зависимости от шага 1 .

Однако при переходе цепи с ведущей на ведомую ветвь растягивающие силы Q i и Q i +1 изменятся на величину каждого значения коэффициента сцепления B i , поэтому его нужно определить точнее.

Построим систему координат ХOY . Она проходит через центр оси вращения эвольвентной звездочки. Вектор оси Х совпадает с вектором линейной скорости зубчатой цепи в передаче.

Проанализируем равновесие первого звена i и второго i + 1 .

Равновесие сил на оси Х ( ∑Х = 0) будет равно:

• -Q+N-Nf-F +F +Q =0 .(2)

i      iX      iX        цiX      цi+1Xi

Равновесие сил на оси Y ( ∑Y = 0) будет равно:

G+G-F-N-Nf+Q -F =0.(3)

зi       зi+1      цiY       iY       iY         i+1Y      ц i+1Y.

При ∑X = 0 и ∑Y = 0 пластины зубчатой цепи будут неподвижны. Если же ∑Х = 0 и ∑Y ≠ 0, то пластины будут двигаться по профилю зуба.

Определим силы, действующие на звенья цепи. На рис. 2 обозначены: P — центр масс звена зубчатой d цепи; dк — диаметр окружности места контакта K пакета пластин с профилем зуба звездочки, d = b ; dд — cosθ диаметр делительной окружности звездочки, d =       .

sin

z

Ниже перечислены силы, действующие вдоль осей координат.

Вдоль оси Х :	Вдоль оси Y :
NiX = Ni ⋅ sin β ,	NiY = Ni ⋅ cos β ,
N iX f = N i f ⋅ cos β ,	N iY f = N i f ⋅ sin β ,
F цiX = F цi ⋅ sin ϕ , F цi + 1 X = F цi + 1 ⋅ sin ϕ , Qi + 1 X = Qi + 1 ⋅ cos ϕ ,	F цiY = F цi ⋅ cos ϕ , F цi + 1 X = F цi + 1 ⋅ cos ϕ , Qi + 1 Y = Qi + 1 ⋅ sin ϕ .

Здесь β — угол профиля зуба эвольвентной звездочки; ϕ= — половина углового шага зубьев эвольвентной z

звездочки. Значения угловых параметров:

λ = ϕ+γ ,                                           (4) µ= π-γ-θ к ,                                       (5) ν=π 2 +γ+θ к ,                                         (6) ρ=π 2 -ϕ+θ к ,                                         (7) β=π 2 -ϕ-γ .                                        (8)

Здесь γ — половина угла заострения зуба эвольвентной звездочки.

γ=α к -θ k .                                             (9) d α= arccos b .                                            (10) к d к

θ к — угол между осью OO i +1 зуба и линией, соединяющей точку K 1 с центром O звездочки (рис. 2).

Машиностроение и машиноведение

• ¹    ГОСТ 13552– 81. Государственный стандарт союза ССР. Цепи приводные зубчатые. Технические условия / Государственный комитет СССР по стандартам. — М.: Изд - во стандартов, 1987. 12 с.

  ⁶ k ⁼ 7 d

  к

  
  

  .

  
  
  
  

S_k — толщина зуба эвольвентной звездочки на месте контакта K с зубчатой цепью (рис. 1). d_b = mzcosa — диаметр основной окружности эвольвентной звездочки, где m — модуль звездочки для передач с зубчатой цепью, z — количество зубьев звездочки.

Подставив все значения, входящие в уравнения (2) и (3), получим:

2 G₃ - F ■ cos ф- NJ ■ sin в- N ■ cos ₽ + Q _+l ■ sin ф- F _j+l ■ cos ф = 0,                  (12)

Q . +1=

(F ■ cos ф + N. ■ cos в + N f ■ sin в + F  ■ cos ф- 2 G ) = —-------:i ::^+:--------- ,                             (13)

Sin ф

Q = N ■ cos в- Nf ■ cos в- F ■ sin ф + F _+l ■ sin ф + Q _+l ■ cos ф = 0.                   (14)

Преобразуя уравнения (13) и (14), получим коэффициент сцепления В зубчатой цепи с заданным зубом эвольвентной звездочки:

Q . N • cos ^{e -} NJ ■ cos ^{e -} F . ■ sin ф + F ■ sin ф + Q , ■ cos ф B i = —- = sin ф (----------------------------------------------------

Q i + 1            J" cos ф ⁺ N * Cos ^{в + N} i ^f ■ sin ^{в +} F ,. + 1 ■ Cos ф - ^{2 G} 3

Если известна величина натяжения ведущей ветви цепной передачи S 1 , то натяжение ведомой ветви S 2 определяется с учетом общего коэффициента сцепления цепи с зубом звездочки:

Bz =    ,(16)

S ₂

S2 =    ,(17)

В

z

B = B■ B. ■ B2...B .(18)

z012

Здесь B z — общий коэффициент сцепления цепи со звездочкой; n — количество зубьев ведущей эвольвентной звездочки.

Результаты исследования. Для проверки расчетов был спроектирован и изготовлен стенд 1 , защищенный патентом Российской Федерации (рис. 3). Проведены стендовые испытания исследуемой цепной передачи. Параметры:

• 1)    мощность электродвигателя N_эл = 12 кВт,

• 2)    шаг зубчатой цепи t_ц = 19,05 мм,

• 3)    количество зубьев ведущей и ведомой звездочки z 1 = z 2 = 23,

• 4)    частота вращения ведущей и ведомой звездочки n 1 = n 2 = 1000 об/мин.

  
  
  

  Рис. 3. Испытательный стенд передачи с зубчатой цепью и эвольвентными звездочками: 1 — ведущая звездочка, 2 — ведомая звездочка, 3 — зубчатая цепь, 4 — электродвигатель, 5 — генератор

  
  

Для стендовых испытаний проводились вычисления с учетом справочных данных 1, 2, 3, 4 . Результаты представлены в таблице 1.

Таблица 1

Полученные данные для определения тяговой способности цепной передачи с зубчатой цепью

Параметр	Обозначение и размерность	Численное значение
Натяжение рабочей ветви передачи	S 1 , H	4662
Натяжение холостой ветви передачи	S 2 , H	270
Общий коэффициент сцепления цепи с ведущей эвольвентной звездочкой	B 1	17,2
Центробежная сила цепи	F ц , H	29,82

Предложенный подход к определению коэффициента сцепления подтвердил верность силового расчета с учетом центробежных сил и коэффициентов трения пакета пластин и зуба звездочки.

Обсуждение и заключения. В данной работе определены все силы, действующие в зацеплении пакета пластин цепи и зуба звездочки. Представлен порядок силового расчета передачи с зубчатой цепью. Получены зависимости для определения влияния центробежных сил и коэффициентов трения на конечный расчет коэффициента сцепления. Для подтверждения теории цепная передача исследована на испытательном стенде.

Итак, центробежные силы и коэффициенты трения при зацеплении существенно влияют на тяговую способность передачи с зубчатой цепью и эвольвентными звездочками.