Силы Лоренца, Ампера и закон сохранения импульса. Количественный анализ и следствия

Известно, что силы Лоренца и Ампера противоречат третьему закону Ньютона, но не противоречат более общему закону сохранения импульса, поскольку электромагнитное поле обладает импульсом. Из этого следует, что эти силы должны уравновешиваться потоком электромагнитного импульса. Однако, насколько известно автору, нет соответствующего количественного сопоставления и поэтому оно рассматривается ниже. При этом, в частности, показывается, что из закона сохранения импульса можно найти некоторые следствия.

Оглавление

• 1.    Вступление

• 2.    Конфигурация поля

• 3.    Сила Лоренца

• 4.    Сила Ампера

• 5.    Обсуждение Литература

2.    Конфигурация поля

1.    Вступление

Известно, что сила Ампера противоречит третьему закону Ньютона, но не противоречит более общему закону сохранения импульса, поскольку электромагнитное поле обладает импульсом. Важно отметить, что стационарное электромагнитное поле также может обладать импульсом, и поэтому сила Ампера не противоречит закону сохранения импульса и в том случае, когда она возникает при взаимодействии постоянного тока с постоянным магнитным полем. Из этого следует, что сила Ампера должна уравновешиваться потоком электромагнитного импульса. Однако, насколько известно автору, нет количественного сопоставления силы Ампера с потоком электромагнитного импульса. Именно это сопоставление и рассматривается ниже. При этом определяются некоторые параметры и с их учетом показывается, что силы Лоренца и Ампера можно рассматривать как следствия существования потока электромагнитного импульса и закона сохранения импульса.

Обозначим для электромагнитного поля: W - плотность энергии (скаляр), кг·м^-1·c^-2, S - плотность потока энергии (вектор), кг·с^-3, p - плотность импульса (скаляр), кг·м^-2·с^-1, f - плотность потока импульса (вектор), кг·м^-1·c V - объем электромагнитного поля (скаляр), м³,

На рис. 1 показаны проводник длиной L с током I , находящийся в магнином поле с индукцией B и двигающийся со скоростью v под дейстаием силы Ампера F . Векторы напряженности E электрического поля, создающего ток, и индукции B взаимно перпендикулярны. Поэтому возникает поток электромагнитной энергии с плотностью S , показанный на рис. 1 окружностями. Можно представить его в виде двух сфер, объединяющихся в теле проводника и пронизывающего проводник в вертикальном направлении. Этот поток эквивалентен потоку электромагнитного импульса f .

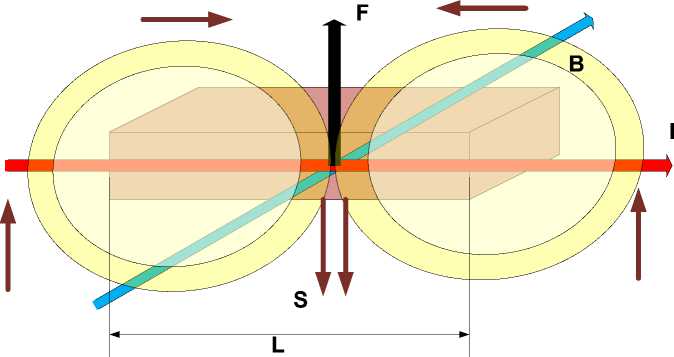
Рис. 1.

Известно [1, 2], что

I f| = W.(1)

S = W • c,(2)

p = W/c, p = S/c2,(3)

• f = P •c, f = S/c .

Интеграл от плотности по объему будем обозначать как

• AV =J A • dV .(4а)

V

Поток энергии SV может существовать и в статическом электромагнитном поле [3]. Следовательно, поток импульса fV существует и в статическом электромагнитном поле, создаваемом постоянным током и постоянным магнитным полем.

Закон сохранения импульса для устройства, взаимодействующего с электромагнитным полем, можно записать в следующем виде [3]:

• -^-J ⁾⁼l ( pv ) + V ,                       (5)

dt       о t где

J – механический импульс устройства,

• V - объем устройства; объем, в котором электромагнитный импульс взаимодействует с устройством (суммарный поток импульса во всем объеме поля равен нулю).

Известно, что сила, действующая на устройство,

F =-^d ( J ) -                                   (6)

d i t

Следовательно,

F =f|(pP-)+ fv 'I -<51         ;

потоке

Объединяя (7) и (3, 4), получаем:

f=f£[Sv]+SV-1 -< dt < c ) c J

Таким образом, если устойство находится в электромагнитной энергии SV , то на него действует сила (8), зависящая только от потока электромагнитной энергии SV . Эта сила существует и при постоянном потоке SV , и тогда

F =     .                                                (9)

c

В том случае, если поток электромагнитной энергии распространяется в веществе с относительными диэлектрической ε и магнитной µ проницаемостями, в формулы (8, 9) вместо скорости света c в вакууме необходимо подставить скорости света в веществе

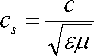
Рассмотрим случай (показанный на рис. 1), когда векторы электрической E и магнитной H напряженностей перпендикулярны. Тогда

5 = EH                                       (11)

Пусть еще поле в устройстве является равномерным и сосредоточено в объеме V . Тогда из (8, 10, 11) получаем:

F = V

I

d dt

ЕНец A c 2 J

+

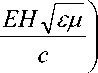
Если, кроме того, поле является постоянным, то

F = VEH 4^1

c

.

3. Сила Лоренца

Рассмотрим магнитную силу Лоренца, действующую на тело с зарядом q , двигающееся со скоростью v перпендикулярно вектору магнитной индукции B :

F l = qvB - (14)

Мы будем пренебрегать индукцией собственного магнитного поля движущегося заряда (по сравннению с индукцией внешнего магнитного поля) и собственным электромагнитным импульсом движущегося заряда. Тогда надо принять, что сила (14) вызвана

потоком импульса электромагнитного поля, пронизывающего тело заряда. При этом из (13, 14) получаем:

FL = VEH 4^

Lc

.

где V – объем тела. Отсюда находим:

EH εµ qvB = V------ c

или, при B = p o pH ,

qvc =

VE ε/µ µo

Следовательно, внутри тела должна существовать напряженность электрического поля, направленная вдоль скорости, и равная

E = qvcMo

V ε/µ

Заметим, что

cµo

^ o - 377 ε o

При этом

E _L =   - 377^ .

µV V

Следовательно, внутри заряженного тела, движущегося в магнитном поле и находящегося под действием силы Лоренца, существует напряженность электрического поля, пропорциональная скорости движения.

Пример с электроном

У него заряд   qo = 1.6 • 10 19, классический радиус ro = 2.8 -10 15, объем, сответствующий этому радиусу, Vo = Arno = 92 -10-45. При этом E L - 7-1026 • v . Можно 3µ таже сказать, что на диаметре электрона вдоль направления скорости существует разность потенциалов

U o = 2 Е 0 Г 0 - 4 • 10¹²

• v.

Рассматривая

напряжение рассуждения

Фейнмана [3] о внутренних силах электрона, удерживающих заряды электрона на поверхности сферы, можно заметить, что это напряжение является той силой, которая "подтягивает" отстающие заряды к своему месту на сфере тогда, когда он движется под действием силы Лоренца.

4.    Сила Ампера

Рассмотрим силу Ампера, действующую на проводник с током I , двигающийся со скоростью v перпендикулярно вектору магнитной индукции B :

F A = IBL .                                            (21)

Если эта сила вызвана потоком импульса электромагнитного поля, пронизывающего проводник, то

FA = vEEH ^л .                             (22) c где V – объем проводника. Отсюда находим: IBL = vEH8                       (23) c или, при B = totH ,

IHLt o t = VEH8 .                     (24) c

Следовательно, напряженность электрического поля в этом случае

	E = ILC t o .                                     (24а) V ε / µ
Если s	- площадь сечения, L - длина проводника, то V = sL .                                                  (25)

Если напряжение на проводнике постоянно и равно U , то

E = U / L .                                              (26)

Если удельное сопротивление проводника равно ρ , то

U = IpLjs = jpL                               (27)

и E = jp                                           (28) Тогда jP = ^sc^                             (29) s ε/µ или 2 8 = 1-^° t.                                        (30) I p ) Таким образом, диэлектрическая проницаемость проводника с током зависит только от µ и ρ .

Например , при ц = 1, р = 2 - 10 ⁶ (ом*м) из (30) находим, что е « 7 - 10¹⁶ .

Для проверки подставим (30) в (22) или в (13) получим

F A = VEH ^ о ^ = — .                     (31)

ρρ и далее с учетом (28) получим (21). Аналогично, подставляя (30, 28)

в (12), получим

F A

H ^

д t   с ( р J

к к            ;

EH Ц'

с

= V

' цц а.V ср д t

EH ^o^

Р 7

+ EH EoE

Р J

или

F = L^P д A    ср д t

(IB )+ IBL.

Следовательно, сила Ампера должна зависить также и от скорости изменения тока и/или магнитной индукции. Эти изменения могут быть вызваны изменением тока, изменением поля или изменением положения тока относительно поля. Практически такая зависимость может быть обнаружена только при очень высокой частоте (из-за коэффициента Цо « 4 -10 15).

c

Подставляя (28) в (31), находим: F = VjB ,

(32а)

где (напомним) V – объем токопровода.

Например , при B = 1 [ r ] j = 4 [ a / sm ² ] = 4 - 10⁴ [ A / m ² ] из (32а)

находим, что F [ N ] = 4 - 10 4 V [ m 3 ] . В частности, при V = 10 ^{- 3}[ m 3 ] находим, что F = 40[ N ] .

5.    Обсуждение

Из вышесканного следует, что силу Ампера можно рассматривать как следствие существования потока электромагнитного импульса и закона сохранения импульса. Но при этом надо еще предположить, что диэлектрическая проницаемость проводника с током зависит от µ и ρ по (30). В этом случае обнаруживается также зависимость силы Ампера от скорости изменения тока и/или магнитной индукции.

Совмещая (20) и (30), найдем

EC ^1 = П^V p 7 V

или

E = qv . (34)

V

Качественно эту силу можно объяснить тем, что свободные электроны "отстают" от тела и скапливаются в "хвосте" ускоряющегося тела – такое явление рассмотрено Фейнманом для ускоряющегося электрона [3]. Электрическое сопротивление материала тормозит равномерное распределение зарядов. На это расходуется дополнительная энергия. Следовательно, движение заряженного тела с постоянной скоростью происходит с затратой энергии на тепловые потери. При этом обеспечивается постоянство энергии электрического поля внутри заряженного тела.

Таким образом, силу Лоренца можно рассматривать как следствие существования потока электромагнитного импульса и закона сохранения импульса. Но при этом придется еще предположить, что внутри движущегося заряженного тела существует напряженность электрического поля вида (34) , пропорциональная скорости движения.