Симметричная потеря устойчивости композитной трехслойной пластины

Одним из наиболее вероятных видов разрушения трехслойных пластин, нагруженных в плоскостях несущих слоев усилиями сжатия или сдвига, является потеря устойчивости. При расчете трехслойных пластин различают несколько форм потери устойчивости, одной из которых является сморщивание несущих слоев с образованием весьма коротких волн, расположенных симметрично относительно срединной плоскости.

Эта форма потери устойчивости называется симметричной и характерна только для трехслойных конструкций, имеющих податливый заполнитель.

Первое исследование сморщивания несущих слоев трехслойной панели было выполнено в 1940 г. [1] с использованием для заполнителя модели упругого основания Винклера. Эта работа была продолжена многочисленными исследователями, результаты работы кото- рых обобщены и представлены в известных монографиях [2–6].

Несмотря на длительную историю, задача о сморщивании несущих слоев трехслойной пластины и в настоящее время привлекает внимание тех, кто занимается проектированием несущих конструкций [7–16]. Это в первую очередь обусловлено использованием в трехслойных пластинах композиционных материалов.

Уравнение устойчивости несущего слоя. Рассмотрим трехслойную пластину, состоящую из двух одинаковых композитных несущих слоев, между которыми расположен ортотропный заполнитель.

Отнесем срединную плоскость пластины к системе ортогональных координат xyz . Обозначим через a и b размеры пластины по осям х и у соответственно, а через h и § — толщины несущего слоя и заполнителя.

Дифференциальное уравнение симметричной формы потери устойчивости получим, используя энергетический метод [18–19]. Потенциальная энергия трехслойной пластины U складывается из потенциальной энергии изгиба несущего слоя при сморщивании U_{f acing}, потенциальной энергии деформации заполнителя U _core и работы усилий U _load, действующих в плоскости несущего слоя, т. е.

U = U facing + U core + U load . (1)

Отметим, что в рассматриваемом случае потери устойчивости потенциальная энергия (1) определяется только для половины трехслойной пластины, лежащей, например, выше срединной плоскости.

При сморщивании ортотропного несущего слоя потенциальная энергия изгиба определяется следующим выражением:

где a x , a y , a _z - нормальные напряжения, действующие в заполнителе вдоль осей х , у , z ; ^т xy , т _xz , ^т yz - касательные напряжения, действующие в плоскостях ху , xz , yz ; e_x , ^e y , e_z – нормальные деформации вдоль осей х , у , z ; ^e xy , e_xz , e yz – деформации сдвига в плоскостях xy , xz , yz .

Напряжения и деформации в ортотропном заполнителе связаны между собой законом Гука

e x

^a x

E x

Ц,, xy _{E y}

ez

0^

^Ц xz^z ’

^a z

E z

U

facing

ab

-1 JJ

Г 8 ² w    „   8² w 8 ² w

¹¹ I   Л 2   I   ^{+ 2} D 12 Л 2  Л 2

(8 x )        8x  8y

⁺ D 22

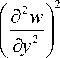
+ 4 D ₃₃

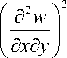
dxdy ,

где w – прогиб несущего слоя, D ₁₁ , D ₁₂ , D ₂₂ , D ₃₃ – изгибные жесткости ортотропного несущего слоя, полученные, например, в монографии [17].

Выражение, определяющее работу усилий, действу-

ющих в плоскости несущего слоя при сморщивании, име-

ет вид

1 ^ab

^U load = J J

^N x ⁰

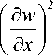
+2N     + nо (^ I xy 8x 8y    y ( 8y )

dxdy ,

где N_x ⁰ , N_y ⁰ – нормальные и N_x ⁰ _y – сдвигающие докрити-

ческие усилия.

Для вычисления потенциальной энергии деформации заполнителя необходимо исследовать характер распространения вглубь заполнителя прогибов несущего слоя при

сморщивании.

В общем случае величина U _core определяется следу-

ющим выражением: δ

ab 2 Г

U core

ab 2

-1 JJJ n n n

0 0 0 \

a ex + “ ey + “ ez + )

xxyyzz

+т e + т e + т e xy xy     xz xz     yz yz )

dxdydz ,

e y

^a y

E y

H« “ x yx _E

x

“^

^{Ц yz} Ez ’

^Ц zx

e xy

a

x

E_x ^т xy G ^, xy

^a y

^Ц zyEy ’

e = ^x^ e exz , eyz

^G xz

^T yz

G yz ^,

где E_x , E_y , E_z – модули упругости материала заполни-

теля в направлениях x , y , z ; G_xy , G_xz , G га в плоскостях xy , xz , yz ; ^Ц yx , ц _xz , ^Ц yx коэффициенты Пуассона.

_yz – модули сдви-

, ^Ц yz , ^Ц zx , ^Ц zy

–

Нормальные и сдвиговые деформации связаны с перемещениями u_x , u_y , u_z вдоль соответствующих коор-

динатных шениями:

^e xy

осей следующими геометрическими соотно-

ex

8 u

x

8x ’

e

8 U y

'y ^- ^’ e_z

8 y     ^z

8 u_z .

8z ’

⁸ u y x

8 y     8 x ’

8 и

8u   8u exz = —- + — , xz

8 z    8 x

8 uy   8 u, eyz =—” + —z". y    8z    8y

При симметричной форме потери устойчивости трехслойной пластины в несущих слоях появляется много мелких волн. При этом, очевидно, тангенциальные перемещения отсутствуют на гребнях волн как в несущих слоях, так и в заполнителе. Поэтому с достаточной степенью достоверности можно принять, что тангенци-

альные перемещения отсутствуют во всем заполнителе. В этом случае

U x - 0, u y ^- 0.

Тогда, с учетом равенств (10) из геометрических соотношений (9) следует

e_x - 0, e y ^- 0, e xy ^- 0;

8u8

zz ez ~ , exz- ,

8z8

Подставляя (11) в (4), получим δ ab2

^U core

e yz

8 u_z

8 y

.

^a z e z ^{+ T} xz e xz ^{+ T} yz e yz ) ^dxdy^dz . (13)

Выразим напряжения, входящие в формулу (13), через деформации. Трансверсальные напряжения найдем из физических соотношений (8), т. е.

^T xz    G xz e xz , ^T y^z   yz e yz yz .

Для определения a _z воспользуемся формулами (5) и (6). Перепишем соотношения (5), учитывая равенства (11), в следующем виде:

^a x

E x

a y a

Цхх  Цхг xy E xz E

“x    ^a y       a_{z      x}

Цхх ""+" + ^^-Цух —z" .

yx _{E E} yz _E ( )

Используя уравнения (15), выразим напряжения а x и а y через напряжение а z и затем полученный результат подставим в равенство (6). После преобразований будем иметь

2 T- 1, ° ' - ' .     '.             ⁽²⁶⁾

Величины R , K и K y являются же сткостными па- zx ^y

Здесь

E z

= E_z 1 -I

^ц zx

а z = E z e z .

^(ц xz ^{+ Ц} yz ^Ц xy ^{) + Ц} zy ^(ц yz ^{+ Ц} yx ^Ц xz

^{1 -Ц} yx ^Ц xy

-1

Это приведенный модуль упругости материала запол-

раметрами заполнителя.

Выражение (24) определяет потенциальную энергию деформации заполнителя в соответствии с моделью, в основу которой положена гипотеза об отсутствии в заполнителе горизонтальных перемещений u_x и ^u y . Складывая уравнения (2), (3) и (24), представим потенциальную энергию трехслойной пластины в следующем виде:

нителя в направлении оси z .

Подставляя равенства (14) и (16) в уравнение (13), получим

δ ab2

^U core = 2 f Й ⁽ E z e^{2 +} G xz e xz ⁺ G yz e 2 ^Z ) dxdydz " (18) 000

С учетом (12) выражение для потенциальной энергии деформации заполнителя (18) примет вид

ab

U = ff Ф

d ² w d ² w d ² w d w d w

₍ d x ² , d y ² , d x d y ’ d x ’ d y ’

w | dxdy

где

Ф = ¹

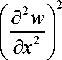
+ 2 D 12

d ² w d ² w "x? S y^r

+ D 22

+

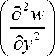
δ ab 2 U- = iJJJ 000

— f d u, ? E z I d z I

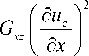
^D 11

+ 4 D 33

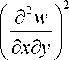
+ R_zw ²

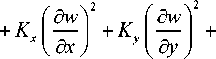
^{+ G} yz

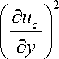
dxdydz . (19)

+ N'x

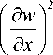
+ 2 № £ w ^ w + N “ f^ w I ^xy d x d y    ^y ( d y )

Как видно из формулы (19), потенциальная энергия деформации заполнителя зависит от нормального перемещения u_z . В рассматриваемой задаче функция u_z должна принимать нулевые значения на срединной плоскости пластины и совпадать с прогибом несущего слоя на

границе раздела, т. е.

[ w (x , y ), z = 5/2

Uz = A z   [0,         z = 0

В положении равновесия потенциальная энергия трехслойной пластины имеет минимум, поэтому прогиб несущего слоя должен удовлетворять следующему дифференциальному уравнению Эйлера:

d ²      5 Ф        d ²

d x ² d ( d ² w /d x ² ) d x d y ^X

Представим перемещение u_z в следующем виде:

u z = f ^{( z} ) w ⁽ x , y ) , ⁽²¹⁾ где f ( z ) задает вид распределения перемещений по толщине заполнителя. Из (20) и (21) следует, что f ( z ) должна удовлетворять следующим условиям:

5 Ф       d ²     5 Ф

X                         I

d ( d ² w /d x d y ) d y d ( d ² w /d y ² )

А /^Ф_x -А /^Ф _x +д Ф = 0.   (29)

d x d ( d w /d x ) d y 5 ( 5 w /d y ) d w

zx [ 1, z = 5 /2

f ( z ) =                             (22)

^V ’ [ 0, z = 0

Зададим f ( z ) в виде

(A - f(z) = |2II .                    (23)

I 5 )

Здесь параметр - характеризует скорость затухания нормальных перемещений по толщине заполнителя. В дальнейшем параметр - будет подбираться из условия минимума усилий, сжимающих несущий слой.

Подставим уравнения (21) и (23) в уравнение (18) и выполним интегрирование по z . В результате получим

Этому уравнению должна удовлетворять функции w ( x , y ) , реализующая экстремум функционала (27). Подставляя (28) в (29), получим

d w         drw      wd

D11 ----"л+ 2(Di 9 + 2D-i-i )---Г---- + D99 T~

¹¹ d x^{4     ( 12      33 )} d x ² d y ^{2     22} d y⁴

- K ^- w + Rw - N_x ¹ ^- w - 2 N 0

^y d y²      z ^x d x ²        xy

d2 w

d x d y

к d 2 w K^x d x²

-

N y ⁰|_T = 0. (30) d y

Уравнение (30) представляет собой основное диффе-

ab

U core = 2 ff

Здесь

R_zw ² + K_x

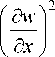
I ^d w I

+ Kyi      I

(d y )

dxdy . (24)

R z = E z |ф⁽- ), K x = G xz jo OY, K y = G yz 2 0 ( - ) , (25)

ренциальное уравнение, описывающее симметричную форму потери устойчивости трехслойной пластины, что сопровождается сморщиванием композитных несущих слоев.

Рассмотрим далее пример по определению критического усилия сжатого несущего слоя трехслойной полосы. Этот пример позволит оценить влияние упругих и геометрических параметров на характер волнообразования и величину критических нагрузок.

Цилиндрическое сморщивание несущих слоев трехслойной полосы. Рассмотрим трехслойную полосу, два противоположных края которой свободны, а по двум дру-

где

гим несущие слои нагружены сжимающими погонными усилиями N.

Очевидно, что сморщивание несущих слоев будет происходить только в направлении оси х. Уравнение устойчивости полосы можно получить из общего уравнения (30), если положить в последнем w = w(x), Nx = -N, N0y = 0, N0 = 0.

Тогда из (30) будем иметь d4w

^{D 11} dx ⁴

-

d2wd

K_x —— + R.w + N —— = 0.

x dx2    z

Для удобства анализа приведем уравнение (31) к безразмерному виду. Заменим координату х на безразмерную координату a по следующей формуле:

a = x /1,(32)

где l – длина полосы в направлении оси х. С учетом равенства (32) уравнение (31) примет вид d4w   d2wd

— - r — + tw ■ n 0, da    da где n - безразмерный коэффициент устойчивости:

П = N12/ D11.(34)

Безразмерные параметры r и t , входящие в уравнение (33), определяется следующими выражениями:

r = Kx12/ D11, t = RZ14/D11.(35)

Пусть несущий слой выполнен из однородного ортотропного материала. Если пренебречь во всей конструкции эффектом Пуассона в направлении оси y , то из-гибная жесткость несущего слоя и жесткости заполнителя могут быть представлены следующими равенствами: D 11 = E x h ³ /12, K x = G xz 5 /2efe ) R z = E z 2/ 8ф ( ^ ), (36) где E_x – модуль упругости материала несущего слоя в направлении оси х .

Подставляя (36) в (35), будем иметь r = pO(^), t = 5ф(^).

Здесь p = 6Gxz IEx - 12/52-83/h3,

5 = 24 Ez I Ex - 14/54-83/h3.(38)

Примем, что на краях полосы a = 0 и a = 1 выполняются условия шарнирного опирания. Тогда решение уравнения (33) будем искать в форме

W = Wm sin Xm a,(39)

где m - число полуволн вдоль координаты a; X _m = m n ; w_m – неизвестное число.

Подставляя (39) в однородное дифференциальное уравнение (33), найдем величину n , при которой это уравнение будет иметь нетривиальное решение, т. е.

n = X m + Г + t / X m .                (40)

Учитывая равенства (37), можно утверждать, что величина коэффициента устойчивости зависит от параметра волнообразования X 2 _m и параметра ^ , определяющего скорость затухания нормальных перемещений по толщине заполнителя. Рассматривая П как функцию X 2 _m и ^ , запишем условие ее минимума в следующем виде:

dn / d(Xm) = 0(41)

и dn / de = 0.(42)

Подставляя (40) в (41), найдем

Xm = Vt.(43)

Учитывая полученный результат, преобразуем равенство (40) к виду n = 2 Vt + r.(44)

Подставляя (37) в (44), будем иметь n = 2 V 5 ф (£) + p 0(^>.

Теперь величина коэффициента устойчивости при известных 5 и p зависит только от параметра ^ . Подставляя (45) в (42) и учитывая равенства (26), получим для определения ^ следующее нелинейное уравнение:

720(^-1)1      I -q = 0.(46)

1 2 с^{- 1} )

Здесь q = p / Vs.(47)

Подставляя (38) в (47), будем иметь

33 Gxz / E 5 /б q=AУ <77hb<48>

Обозначим корень уравнения (46) через ^ cr . Подставляя ^ = ^ cr в (45), получим выражение, определяющее критический коэффициент устойчивости, т. е.

Псг = 2 V 5 ф (^cr) + p 0(^сг).(49)

Здесь

ф(^cr ) = ^c2r/2^cr -1,

Учитывая равенства (38), представим формулу (49) в следующем виде:

Псг = 12/ 52Ф cr.

Здесь

Vcr = 25 / h \2^6E_z I Ex -8 / h -ф(^сг) + 3G_:(Z I Ex -8²/ h²efer)). (52)

Определим далее критическое усилие при котором происходит сморщивание несущего слоя. Из (34) найдем

Ncr =Псг D11/12.(53)

Для критического усилия справедлива следующая формула:

Ncr = ^crh,(54)

где a_cr - критическое напряжение.

Подставляя (54) и (51) в (53) и учитывая первое из равенств (36), будем иметь acr = Ex ecr.(55)

Здесь ecr =v cr/(1282/ h2).

Будем в дальнейшем называть e_cr критической деформацией.

Учитывая выражение (52), преобразуем уравнение (56) к виду еСг=ЛF Ez^E^ фОи) +1 Gxz / Ex -8 / h • e(^cr). (57)

cr                          cr          xz x              cr

V 3   8 / h            2

Таким образом, критическое напряжение, при котором происходит потеря устойчивости несущего слоя трехслойной полосы, может быть найдено из равенств (55) и (57). Величина acr при заданном модуле упругости Ex определяется величиной критической деформации есг. Из формул (46), (48) и (57) следует, что есг зависит от трех параметров: Ez /Ex , Gxz /Ex и δ/h . Отметим, что критическая деформация, а значит, критическое напряжение, не зависят от l/δ .

Покажем, что с ростом δ/h критическая деформация ε_cr стремится к некоторому пределу, величина которого зависит от отношений модулей упругости. Для этого вернемся к формуле (45), определяющей коэффициент устойчивости η после его минимизации по λ²_m . Величина η при известных s и p зависит в этой формуле только от параметра ξ . Получим формулу, определяющую критический коэффициент устойчивости для трехслойной полосы с толстым слоем заполнителя, т. е. с большим отношением δ /h . В этом случае следует принять ξ →∞ . Тогда из равенств (26) будет иметь

ϕ(ξ)=ξ/2, θ(ξ)=1/2ξ.(58)

Подставляя (58) в (45), получим

η = 2sξ + p/2ξ.

Реализуя условие (42), найдем

ξcr =3 p2/2s.

Тогда

ηcr = 3 3 ps.

лI4

Подставляя (38) в (61), будем иметь ηcr=l2/δ2ψcr.

Здесь

ψ = 6 δ2/h2 318G /E ⋅E /E .(63)

cr                             xz x z x

Учитывая равенства (63), из (56) получим

εcr = 3I-9 3 G /E ⋅ E /E .

cr                 xz x z x

Уравнение (64) определяет предельное значение критической деформации, величина которой зависит только от отношений модулей упругости. Подставляя (64) в (55), получим для определения критического напряжения следующее уравнение:

σcr=0,82548 ³ExGxz Ez.            (65)

Отметим, что равенство (65) с тем или иным численным коэффициентом встречается как в известных монографиях [2–6], так и в современных исследованиях [11–16].

Из вышесказанного следует, что определение критических напряжений необходимо выполнять с учетом величины отношения δ /h . При δ/h > 30 можно воспользоваться формулой (65). Если отношение δ/h< 30, то более точное значение σ_cr дадут формулы (55) и (57).

Найдем теперь число полуволн, образующихся при сморщивании несущего слоя. Учитывая, что λm = mπ , из (43) будем иметь m = 4 t /π.                    (66)

Подставим второе из равенств (37) при ξ = ξcr в уравнение (66). Тогда mcr =4 sϕ(ξcr) /π .                (67)

Выполним далее анализ влияния упругих и геометрических параметров трехслойной полосы на число полуволн mcr . Подставляя s из равенств (38) в формулу (67), будем иметь

l mcr = δ γcr. (68)

Здесь

γcr =1/π⁴24Ez/Ex⋅δ³/h³⋅ϕ(ξcr). (69)

Как видно из уравнения (68), величина m_cr прямо пропорциональна l/δ .

Из анализа полученных данных следует, что величина γ_cr , а значит, и m_cr , зависит от δ /h практически линейно как для податливого заполнителя, так и для жесткого заполнителя.