Симметричные колебания трехслойной пластины

Колебания трехслойных пластин отличаются большим разнообразием форм движения несущих слоев и заполнителя. Наиболее изученными из них являются поперечные изгибные колебания, при которых оба несущих слоя и заполнитель движутся в одну сторону. Вместе с тем трехслойные пластины могут совершать колебания, формы которых отличаются от форм поперечных колебаний. К ним относятся симметричные колебания трехслойных пластин с одинаковыми несущими слоями. При таких колебаниях срединная плоскость пластины не движется, а несущие слои и части заполнителя, лежащие по разные стороны срединной плоскости, движутся в противоположных направлениях. Очевидно, что для моделирования симметричных колебаний трехслойных пластин необходимо учитывать податливость заполнителя. Отметим, что число исследований, в которых рас- сматривается влияние податливости заполнителя на динамическое поведение трехслойных пластин, невелико. Одним из первых было исследование, выполненное Фростингом и Томсоном [1]. Анализ решенных к настоящему времени вибрационных задач, в которых учитывается влияние податливости заполнителя на динамическое поведение трехслойных пластин, позволяет сделать вывод, что эти исследования далеки от своего завершения и могут быть дополнены новыми результатами.

Уравнения движения. Рассмотрим трехслойную пластину, состоящую из двух одинаковых композитных слоев и ортотропного заполнителя. Введем декартову систему координат x , y , z , связанную со срединной плоскостью трехслойной пластины. Пусть a , b – размеры пластины по осям x и y , а t , h – толщины несущего слоя и заполнителя.

Для получения дифференциального уравнения симметричных колебаний трехслойной пластины воспользуемся вариационным принципом Гамильтона [2] . Отметим два положения движущейся пластины – в момент времени τ 1 и в момент времени τ 2 . При этом τ 2 > τ 1 . Рассмотрим далее интеграл действия Гамильтона

пряжения; e_x , e_y , e_z – продольные деформации; e_xy , e_xz , e yz – деформации сдвига .

Компоненты напряжений и деформаций в ортотропном заполнителе связаны между собой законом Гука:

S = J Ldt ,              (1)

т где L – функция Лагранжа, определяемая следующим образом:

L = T – U ,              (2)

ex = °x I Ex — Vxy°y I Ey — VxzCTz I Ez ,(9)

ey = °y I Ey - V yx ° x I Ex — V yz ° z / Ez , ez =°z / Ez -Vzx°x / Ex -Vzy °y / Eyz, exy =T xy I Gxy , exz =Txz / Gxz ,   eyz =Tyz I Gyz ,

где Т – кинетическая и U – потенциальная энергии трехслойной пластины, совершающей симметричные колебания.

Кинетическая энергия пластины определяется формулой

T = T t + T h ,               (3)

где T t – кинетическая энергия несущего слоя; T h – кинетическая энергия заполнителя.

Для потенциальной энергии трехслойной пластины будем иметь

где Е x , Е y , Е z – модули упругости материала; G xy , G xz , G yz – модули сдвига; ν xy , ν xz , ν yx , ν yz , ν zx , ν zy – коэффициенты Пуассона.

Деформации и перемещения в заполнителе связаны между собой геометрическими соотношениями er =дu_ I дx,   e„ =дu„ I дy, e, =дu, I дz, xx  yy  zz e„, =дux Iдy + дu„ Iдx, e„ =ди Iдz + дu, Iдx,(13)

xy x             y            xz xz e„r = дu„ I дz + ди, I дy. yx yz

U = U t + U h ,            (4)

где U t – потенциальная энергия изгиба несущего слоя; U_h – потенциальная энергия деформации заполнителя.

Определим значения кинетической T_t и потенциальной U_t энергий несущего слоя, который совершает изгибные колебания. Выражения для T t и U t будут иметь следующий вид:

ab

T = t b p t Ш⁵ w ^{I dT} ) ² dxdy ;

2    00

ab

ab

U t = 1 JJ D

f^ w 1

¹¹ Id x ² J

д ² w д ² w дx ² д y²

+ D ₂₂

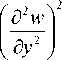
+ 4 D 33

+ 2 D 12

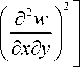
dxdy ,

где τ – время; w = w ( x , y , τ) – прогиб несущего слоя; D 11 , D 22 , D 12 , D 33 – изгибные жесткости ортотропного несущего слоя; B ρ t – инерциальный параметр несущего слоя [3].

Кинетическая и потенциальная энергии заполни-

теля как трехмерного ортотропного тела определяют-

ся следующими выражениями:

a b h /2

T h = 1 JJJ p h

00 0

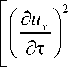
1 ab

| ^д u 1    f д u_z 1

+ 1 Ty I +1 I l дт J V дт J

dxdydz ; (7)

U h  ^1 ° x e x + ° y e y + ° z e z ⁺

+т e , + t e_r + т „ e ^J dXdydz , xy xy xz xz yz yz              ,

где ρ h – плотность материала заполнителя; u x , u y , u z – перемещения вдоль осей x , y , z ; σ x , σ y , σ z – нормальные напряжения; τ xy , τ xz , τ yz , – касательные на-

Напряжения, деформации и перемещения, возникающие в заполнителе, являются в общем случае функциями трех координат и времени. Это обстоятельство существенно затрудняет получение как аналитического, так и численного решений рассматриваемой динамической задачи. Однако симметричные колебания обладают особенностью, которая позволит значительно упростить исходные уравнения для заполнителя. Дело в том, что при таких колебаниях перемещение u z значительно больше перемещений u x и u y , появление которых обусловлено только эффектом Пуассона. Поэтому в рассматриваемой задаче можно принять, что в заполнителе тангенциальные перемещения отсутствуют, т. е.

u_x = 0, u_y = 0.                 (14)

Отметим, что при симметричных колебаниях допущение (14) будет заметно нарушаться только в небольшой области около краев заполнителя х = 0, a и y = 0, b.

Подставляя равенства (14) в геометрические соотношения (13), будем иметь ex = 0,    ey = 0,(15)

exy = 0,(16)

ez =дuz I дz, exz =дuz I дx, evz =дuz I дy.(17)

z z            xz z             yz z

C учетом уравнений (15) и (16) выражение (8), определяющее потенциальную энергию деформации заполнителя, примет вид

1 a b h /2

U =^1'1' (°_z e_z ^+Tx exz ^+Tx exz +т„ e_xZdi:ddddz .   (18)

z z xz xz xz xz yz yz

Выразим напряжения, входящие в формулу (18), через деформации. Для определения σ z воспользуемся соотношениями (9) и (10). Учитывая равенства (15), из уравнений (9) выразим напряжения σ x и σ y через напряжение σ z . Подставляя полученный результат в формулу (10), будем иметь

ст z = E _z e_z ,                  (19)

где Ez – приведенный модуль упругости материала заполнителя в направлении оси z:

E = E _z Г ¹ - ^v к + v v ) + z z          zx xz yz xy

+v fv +v v W1 -v v H zy \ yz yx xz ' \ yx xy / I

Трансверсальные напряжения τ _xz и τ _yz определим из физических соотношений (12):

^T xz    G xz e xz ,    ^T yz    G yz e yz .              ⁽²¹⁾

Подставим равенства (19) и (21) в формулу (18) и заменим деформации, используя геометрические соотношения (17). Тогда для потенциальной энергии деформации заполнителя будем иметь

U h = ¹ i И Г E z ( ^d u / ^d z ) ² + G xz ( ^d U^{1 d} x ) 2 +

2 0 0 0 L

+ G _yz ( d u _z / д y ) 2 ddxddd z .

Подставляя равенства (14) в формулу (7), получим

Th =1J J J P* (d11 / dT)2dxdydz.(23)

Таким образом, потенциальная и кинетическая энергии заполнителя зависят только от перемещения uz. При симметричных колебаниях трехслойной пластины функция uz должна удовлетворять следующим условиям:

/ x [ w ( x , y , t) , z = h /2, u z ⁽ x , y , z , ^tM

[ 0,               z = 0.

образом, параметр ξ позволяет изменять размеры зоны заполнителя, в которой происходит затухание перемещения u z . Величина ξ будет вычисляться в процессе определения частоты симметричных колебаний трехслойной пластины.

Подставляя равенства (25) и (26) в выражения (22) и (23) и выполняя интегрирование, получим ab

U h = I ii

R _z w ² + K x

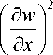
+ K I? ) (^д y )

dxdy ;

ab2

Th = 7 Bp J Лзт1 dxdy.(28)

0 0 v71/

Здесь

Rz = Ez(2/h)ф(^), Kx = Gxz (h/2)0(^),

K y = G yz ( ^h /W ) ,

Bph =ph (h/2)0(^).(30)

Функции φ(ξ), θ(ξ) определяются следующим образом:

Ф(^Н2/(2^-1), 0(^) = 1/(2^ +1).(31)

В равенствах (29) и (30) R z , K x , K y – жесткостные параметры заполнителя; B _{ρ t} – инерциальный параметр заполнителя. Выражения (27) и (29) определяют потенциальную энергию деформации и кинетическую энергию заполнителя в соответствии с допущением об отсутствии тангенциальных перемещений при симметричных колебаниях пластины.

При известных значениях потенциальной и кинетической энергий несущего слоя и заполнителя определим функцию Лагранжа для всей пластины. Подставляя уравнения (3), (4) в равенство (2), получим

L = T t + T h – ( U t + U h ). (32)

Учитывая эти условия, представим перемещение u z в следующем виде

U z ( x , y , z , t ) = f ( z ) w ( x , y , t ) .    (25)

Здесь функция f ( z ) задает характер распределения перемещений u z по толщине заполнителя. Из уравнений (24) и (25) следует, что f ( h/ 2) = 1 и f (0) = 0. При этом зависимость f ( z ) должна обладать возможностью регулировать закон затухания перемещения по толщине заполнителя. Поэтому зададим f ( z ) в следующем виде:

f ( z ) = ( z / ( h /2 ) ) * ,                (26)

где ξ – неизвестный, подлежащий определению параметр, который задает характер затухания нормального перемещения по толщине заполнителя. Изменение параметра ξ приводит к изменению характера затухания перемещения u z от величины прогиба несущего слоя w до 0. При ξ = 1 функция f ( z ) определяет линейный закон затухания u z по толщине заполнителя. При ξ > 1 основное затухание u z происходит в сужающейся зоне, которая приближается к несущему слою пластины. При ξ < 1 зона затухания u z увеличивается и смещается к срединной плоскости пластины. Таким

Учитывая формулы (5), (6), (27) и (28), представим функцию Лагранжа (32) в следующем виде:

т Hz^ I d ² w d ² w d ² w d w d w d w I , , L = Ф| —г,—г,--- ,—, —, —, w | dxdy .

** (d x ² d y ² d x d y d x d y дт )

Здесь

Ф =

I +

d ² w d ² w   „ | d ² w |         | d ² w |

+ 2 D_n         + D_??         + 4 D.,.,          +

¹² d x ² d y ^{2     22} (d y ² 1       ³³ (d x d y )

i (aw i aw

+Rw2 + KI ^w I + K Pw zx   y

( d x )      ( d y J

Подставляя (33) в (1), будем иметь

.

Ш . I д ² w д ² w д ² w д w д w д w I , , Ф1 —_r,—_r,---, —, —, —, w | dxdy .

_т 0 0 ( д x ² д y ² д x д y д x д y дт )

В соответствии с принципом Гамильтона, интеграл действия (35) в промежутке времени τ 2 – τ 1 для действительного движения трехслойной пластины

имеет стационарное значение. Тогда вариация функционала (35) равна нулю, т. е.

5 S = 0.

Приведем уравнение (42) к безразмерному виду. Для этого умножим его на a ² b ² и разделим на (D 11 D 22 )^1/2. В результате преобразований получим

Уравнение, описывающее симметричные колебания трехслойной пластины, является уравнением Эйлера для функционала (35). Это уравнение имеет следующий вид:

η mn = ζ mn γ mn .

д ²

дФ

д ²

дФ

+ дx д (д2w / дx2)   дxду д (д2w / дxду)

+

д ²

дФ

д у ² д ( д ² w / д у ² )

—

д

дФ

д x д ( д w I д x )

—

Здесь

Z _mn = n ⁴ ( a m ⁴ + 2 p m ² n ² + n ⁴ / a ) ,

Y mn = ^{1/1 + r} p ( ^{1 + П} 2 r x ^a m ^{2 + Г} у ^{П 2/} a / ^Z mn ⁺ t z / ^Z mn ) , a = 4 D ₁₁/ D ₂₂ b ²/ a ², ₽ = ( D ₁₂ + 2 D ₃₃ ) / D ₁₁ D ₂₂, r x = K x a ²/ D 11 , Г у = К у Ь ²/ D 22 , t z = R z a²b ²/ V D_nD 22 , r ,= B p h / B p t , П mn =®m_n B p t a ^{2 b 2 /} V ^D 11 ^D 22 .

д дФ ду д(дwIду)

д дФ +дФ дт д ( д w I дт ) д w

Подставляя (34) в (37), будем иметь

D ₁₁ д ⁴ w / д x ⁴ + 2 ( D₁₂ + 2 D 33 ) д ⁴ w I д x ² д у ² +

+ D ₂₂ д ⁴ w I д у ⁴ — K x д ² w I д x ² — К_у д ² w I д у ² + (38) + R z w + ( B р t + B р h ) д ² w I дт ² = 0.

Уравнение (38) представляет собой основное дифференциальное уравнение симметричных колебаний трехслойной пластины.

Рассматривая свободные колебания трехслойной пластины, представим прогиб несущего слоя в следующем виде:

w ( x , у , т ) = w ( x , у ) e ™^т ,            (39)

где i – мнимая единица; ω – круговая частота колебаний; w ( x , y ) – функция формы, описывающая моды колебаний несущего слоя.

Получим уравнение для определения формы несущего слоя при симметричных колебаниях. Подставляя (39) в (38), будем иметь

D ₁₁ д ⁴ w I д x ⁴ + 2 ( D ₁₂ + 2 D ₃₃ ) д ⁴ w I д x ² д у ² +

+ D ₂₂ д ⁴ w I д у ⁴ — K_x д ² w I д x ² — К_у д ² w I д у ² + (40)

⁺ R z w ^— ( B р t ⁺ B p h ) ® ^{2 w} = 0.

Здесь и далее w = w ( x , y ).

Трехслойная пластина с шарнирно-закрепленными несущими слоями. Определим частоту симметричных колебаний трехслойной пластины, у которой края несущих слоев шарнирно закреплены. Представим решение уравнения (40) в следующем виде:

w = EZ w_m „ sin X _mx sin X _пу ,     (41)

m = 1 n = 1

где m , n – число полуволн вдоль осей x и y соответственно; λ m = m π /a , λ n = n π /a , w mn – неизвестные числа.

Подставляя (41) в (40), получим

D ii X ⁴ m + 2 ( D 12 + 2 D 33 ) x m X n + D 22 X 4 —

2        2                       2    (42)

—KxX m — КуX n + Rz = ( Bpt + Bph ) tomn , где ωmn – частота колебаний, соответствующая номерам mn.

Равенство (48) определяет безразмерный частотный параметр η mn несущего слоя как отдельной пластины, не связанной с заполнителем. В формуле (43) величина γ _mn характеризует степень влияния заполнителя на частотный параметр несущего слоя. Величина ζ mn при этом определяет частотный параметр только пластины несущего слоя. На самом деле, если заполнитель отсутствует, то из формул (29), (30) и (47) следует, что r x = 0, r y = 0, t z = 0 , r ρ = 0. В этом случае из равенства (45) будем иметь γ mn = 1. Тогда η mn = ζ mn . Используя формулы (29) и (30), представим равенства (47) в следующем виде:

rx = P x 6^(Z) , ^Г у = Р у 6^(Z) ,                ₍₄₉₎

t z = s z ф ( ^ ) , r p = P p 6 ( ^Z ) .

Здесь px = Gxzha2/(2D11), py = Gyzhb2/(2D22), sz = 2Ēa2 b2/(h(D11 D22)1/2),

P p = P h h / ( 2 B p t ) .                    (50)

Подставляя (49) в (45), будем иметь

Y mn ( ^Z ) = ^{1 +} 0 ( ^ ) ^П 2 ( P x ^a m ^{2 +} Р у ^{П 2} / ^a ) /

/ Z mn +Ф® S z I Z mn ] / ( 1 + P p 6 ( Z ) ) .

Учитывая равенство (51), запишем выражение (43) в следующем виде:

^П mn   ^Z mn ^Y mn ^{(Z) .}

Таким образом, частотный параметр зависит от параметра ξ, который задает характер затухания нормального перемещения по толщине заполнителя.

Определим частоту симметричных колебаний трехслойной пластины. Из равенства (48) будем иметь

Jri

\ I mn у 11   22

^ab \   B p t

Подставляя (52) в (53), получим tomn =Vmn (Z)tomnt,                  (54)

где ψ mn (ξ) = (γ mn (ξ))^1/2. Величина ω mnt , представляющая собой частоту колебаний только пластины несущего слоя, определяется следующим выражением:

_ ^ mn  У ^D 11 ^D 22

ab N   B p t

Подставляя D ₁₁ и D ₂₂ из (58) и B _{ρ t} из (60) в выражение (55), получим

где λ _mn= (ζ _mn ) .

Из формулы (54) видно, что частота симметрич-

^to mnt   ^ mn

t      E xt E yt

ных колебаний трехслойной пластины зависит от величины ξ. Истинное значение частоты колебаний для каждой комбинации m и n может быть получено с помощью процедуры минимизации по параметру ξ. В этом случае

ab^ 12 p _t

Формула (64) определяет частоту колебаний однородного ортотропного несущего слоя.

Если несущие слои выполнены из изотропного материала, то для модулей упругости будем иметь

где

to = m to                    (56)

mn t mn mnt ,                     x 7

Ф mn = min 0 mn ^(S)] ,             ⁽⁵⁷⁾

^S l -S-S r

Ext = Eyt = Et,(65)

Ext = Eyt = Et,(66)

Extvxyt _Etvt,   Gxyt _0,5(1 -vt)/Et,(67)

где ξ r – ξ l – диапазон изменения параметра ξ.

Формула (56) определяет частоту симметричных колебаний трехслойной пластины. Как видно, частота колебаний ω mn представляет собой произведение частоты колебаний несущего слоя ω mnt и частотного коэффициента φ _mn , который учитывает динамическое поведение заполнителя. Отметим, что формула (56) оказывается особенно удобной для параметрического

где E t = E_t (1 -v 2 ); E_t - модуль упругости; v _t - коэффициент Пуассона.

Подставляя (65), (66) и (67) в равенства (61), получим

a_ b ²/ a ², p_ 1.       (68)

анализа, в котором исследуется влияние геометрических, упругих и инерциальных параметров трехслойной пластины на частоты колебаний.

Получим расчетные формулы для трехслойной пластины с однородными ортотропными несущими слоями. Изгибные жесткости такого несущего слоя определяются следующим образом:

C учетом соотношений (66), выражения (62), определяющие безразмерные параметры p x , p y и s z , примут следующий вид:

G ha

P x _ 6 "^x"--^:

x E _t t t

2 ,

p y

E z a ² b ²

sz _ 24=— z        Et t2 t2

h

t

= ₆ GLhbl

E_t t t 2 ,

. -1

.

D 11 = Et 3 /12, D 12 _ E xt V xytt ³/12,

D 22 _ E f t 712, D 33 _ G xyt t ³/12,

E xt = E xt / ( 1 -V xyt V yxt ) ,

E yt = E yt / ( 1 -^V xyt V yxt ) ,

Подставляя (66) в (64) для частоты колебаний изотропного несущего слоя, будем иметь t    Et to mnt =^ mn^-J ?;;—.               (70)

ab у12 p _t

где E xt , E yt – модули упругости; G xyt – модуль сдвига; ν xyt , ν yxt – коэффициенты Пуассона. Для инерциального параметра однородного несущего слоя будем иметь

B p t _p t t ,                      (60)

где ρ t – плотность материала несущего слоя. Подставляя (58) и (59) в (46), получим

^a   У E xt / E yt ^b 7 a ²,

₽ = ( E xt v xyt + 2 G xyt ) У E xt / E yt .

Структуры трехслойных пластин с композиционными несущими слоями и ортотропным заполнителем обладают большим разнообразием геометрических, упругих и инерциальных параметров. Каждый из этих параметров тем или иным образом может влиять на частоты симметричных колебаний. Исследование такого влияния в общем случае является достаточно громоздкой задачей. Для того чтобы сделать параметрический анализ обозримым и в то же время продемонстрировать возможности разработанной динамической модели, рассмотрим далее квадратную трехслойную пластину с изотропными несущими слоями и изотропным заполнителем. Получим расчетные формулы для такой пластины. Пусть в заполнителе

Определим далее безразмерные параметры p x , p y , s z , p ρ . Учитывая формулы (58) и (60), из равенств (50) будем иметь

G ha p _ 6 x-- x       tt

^G yz h b ^{2 p} y = 6^7^, E yt t t

Ex = Ey = Ez = Eh,(71)

Gxy = Gxz = Gyz = Gh,(72)

Vxy = Vxz = Vyx _ Vyz _ Vzx = Vzy = Vh ,

E z     a ² b²(h

24                     1-| ,

У E xt E yt t t I t J

P p

1 p h h

2 p t t

где E h , G h , – модули упругости; ν h – коэффициент Пуассона изотропного материала заполнителя.

С учетом равенства (71) и (73) выражение (20), определяющее приведенный модуль упругости материала заполнителя, примет следующий вид:

E h _ E h [ 1 - 2 v h / ( 1 -v h ) ]7        (74)

Подставляя (72) в (69) и учитывая, что a = b и

E z = E h , получим

G ha ²

px = p y = p = ⁶     T,

E t t t

E h a ⁴ Ш s_z = s = 24 - ^z E. t ⁴ 1 t )

.

Определим далее для рассматриваемой пластины параметры ζ mn , λ mn и γ mn (ξ) . Из первого равенства (68) при a = b будем иметь α = 1. Подставляя α = 1 и β = 1 в уравнение (44), получим

^Z mn ^ ( m ² + n ² ) ² . ⁽⁷⁶⁾

Тогда

^X mn = ^n = ^П ( m ² + n ² ) .

Подставляя α = 1, p_x = p_y = p , s_z = s в уравнение (51) и учитывая равенство (76), будем иметь

Y mn ( S ) = [ 1 + P 6^) / X mn + S Ф ( ^ ) / Z mn ] / / ( 1 + P P ⁶ ( ^ ) ) .

Частота колебаний квадратного изотропного несущего слоя может быть получена из формулы (70), если в ней принять a = b . Тогда

® mn, = X mn ^jT E ¹- .    (79)

a \ 12 p _t

Частота колебаний трехслойной пластины определяется по-прежнему с помощью формулы (56).

Сделаем еще одно упрощение при решении рассматриваемой задачи. Будем в дальнейшем отыскивать частоты колебаний только для случая, когда m = n . Получим необходимые расчетные формулы, заменяя при этом получающийся двойной индекс mn на одинарный индекс m . Из уравнений (76), (77), (78) и (79), полагая в них m = n , получим

Z m = 4 ~ 4 m ⁴, X m = 2n2 m ²,        (80)

Y m ( S ) = [ 1 + P 6 (У / X m + S Ф ( ^ ) / Zm ] / ( 1 + P p 6^ ) ) , (81)

® m, =X m^JzE¹- .     (82)

a \12 p ,

Частота симметричных колебаний рассматриваемой трехслойной пластины может быть найдена из следующих формул (см. уравнения (56), (57):

®m =Фm «mt,

Фm = “in Vm (^) ,

Sl ^S^Sr где

Vm (S) = 7US).(85)

Рассмотрим порядок определения частоты колебаний для произвольного номера m. Пусть известны размеры a, h, t, упругие характеристики Et, νt, Eh, νh (или Gh) и плотности ρt, ρh. С помощью формул (63), (75) определим безразмерные параметры pρ, p, s. Затем используя равенства (31), (81), (84), выполним процедуру минимизации функции ψm(ξ) по параметру ξ и найдем коэффициент φm согласно формуле (84). Завершая вычисления, определим частоту ωmt (82) и частоту симметричных колебаний трехслойной пластины ωm (83).

Выполним верификацию разработанной модели симметричных колебаний трехслойной пластины. Для этого сравним частоты колебаний, в одном случае полученные с помощью этой модели, а в другом – с помощью метода конечных элементов. Пусть рассматриваемая трехслойная пластина имеет a = 0,2 м; h = 0,04 м; t = 0,000 5 м;     E_t = 69 ГПа;     v _t = 0,33;

E_h = 165МПа; v р = 0,031 25; p _t = 2 700кг/м 3 ; p _h = 30кг/м 3 . Определим в примере частоту колебаний f m = ω m / 2π для m = 1, 3, 5. Результаты расчетов, полученные с помощью разработанной модели, имеют следующие значения: f 1 = 11 800 Гц, f 3 = 13 184 Гц, f 5 = 15 469 Гц.

Для определения частот колебаний с помощью метода конечных элементов был использован пакет COSMOS/M. Пластины несущих слоев моделировались элементами SHELL4, а трехмерный заполнитель моделировался элементами SOLID.

Результаты вычислений частот с использованием конечно-элементного моделирования обозначим /mFEM (m = 1,3,5). Были получены следующие значения частот колебаний:     fFEM = 11 803 Гц, f ,FEM = 13 191 Гц , fFEM = 15 483 Гц .

Сравнение частот колебаний f_m и f_m ^FEM ( m = 1,3,5) показывает, что относительная разница между ними составляет 0,025; 0,054; 0,090 % соответственно. Это дает основание утверждать, что разработанная модель позволяет с высокой точностью определять частоты симметричных колебаний трехслойной пластины. Частотный анализ, выполненный по приведенным выше формулам, требует минимальных вычислительных ресурсов, не сравнимых с вычислительными ресурсами, необходимыми для решения этой задачи методом конечных элементов. Преимущества разработанной модели будут особенно заметны в высокочастотном вибрационном анализе. При высокочастотных колебаниях длина полуволны становится заметно меньше толщины заполнителя. Если такую задачу решать методом конечных элементов, то для реалистичного описания движения трехмерного заполнителя надо будет использовать элементы очень малого размера. Это потребует значительных вычислительных ресурсов и увеличит время решения.

Таким образом, решена задача о симметричных колебаниях трехслойной пластины, структура которой состоит из двух одинаковых композитных несущих слоев и ортотропного заполнителя. С использованием вариационного принципа Гамильтона получено дифференциальное уравнение, описывающее движение трехслойной пластины. При выводе этого уравнения были использованы два предположения, касающиеся деформирования заполнителя. Согласно первому предположению, в заполнителе отсутствуют тангенциальные перемещения. В соответствии со вторым предположением нормальные перемещения в заполнителе изменяются от прогиба несущего слоя до нуля по нелинейному закону. Были получены формулы, определяющие частоту симметричных колебаний трехслойной пластины, у которой края несущих слоев шарнирно закреплены. Показано, что частота колебаний трехслойной пластины может быть представлена в виде произведения частоты колебаний несущего слоя и частотного коэффициента, который учитывает динамическое поведение заполнителя. Приведены формулы, определяющие величину частотного коэффициента для трехслойных пластин с ортотропными и изотропными несущими слоями. С помощью метода конечных элементов была выполнена верификация разработанной модели симметричных колебаний трехслойной пластины. Из сравнения результатов вычислений следует, что полученные в работе формулы позволяют с высокой достоверностью определять частоты симметричных колебаний трехслойных пластин. Разработанная модель дает возможность находить частоты с точностью, сопоставимой с точностью аналогичных расчетов, выполненных в пакетах COSMOS/M, ANSYS. При этом частотный анализ, выполненный на основе представленной модели, требует минимальных вычислительных ресурсов.