Simulation of a long-haul fiber optic link with a two-mode optical fiber

Nowadays modern telecommunication networks approach to capacity crunch, which is associated with so-called nonlinear Shannon limit, and a passage to fiber optic links with a few-mode optical fibers is considered as one of alternative solutions for described problem concerned with high nonlinearity of conventional commercial single-mode optical fibers [1–4]. At that time there are various known designs of few-mode optical fibers [5–8] as well as recently published works presenting experimental results demonstrating their potentialities for long-haul fiber optic links [9–12]. A lot of models of long-haul fiber optic links with few-mode optical fibers were developed and based on them simulations were performed to research few-mode optical fiber transport network features.

For example, work [5] presents results of mentioned simulations for two-mode optical fibers. Here just only one guided linearly polarized mode ( LP 01 or LP 11 ) satisfying to cut-off condition was utilized for channel data transmission, and computed results showed advantages in comparison with conventional single-mode optical fibers.

Also in few-mode optical fibers it is possible to utilize particular mode combinations as well as optical vortices [13–17]. Some works [8, 18, 19] announce that optical vortices modes are more resistant to perturbations, therefore they are more preferable for optical channel data transmission in telecommunications. This fact makes interesting the comparison between using of guided modes with particular order and application of optical vortices for optical channel data transmission over long-haul fiber-optic links with a few-mode optical fibers.

Presented work is concerned with described problem for 6000 km length long-haul fiber-optic link with two-

mode optical fiber and 100-km-per-span Erbium doped fiber optic amplifiers system under 100 Gbps DP-DQPSK data transmission.

Model of fiber-optic link with few-mode optical fibers

We utilized well known system of coupled nonlinear Schrödinger equations to describe propagation of optical pulses over few-mode optical fiber, which was written in the following form [5, 20–25]:

j _∂ ^lz ^{, m} + j ^β 1 l , m _∂ ^lt ^{, m} + ^β 2 l , m _∂τ ^l 2 ^{, m} + j α l , m A l , m +

+Y- TAlm- ZZ Q .„|A L| = 0;

2 ⋅ Rl,m p q

C l , m ; p , q

∞

∞

∞

∞

J J I E / , m |² J ^E ; , q ^d * d y

-∞ -∞ 0

∞

∞

J J | E / , m |'d * ^d y I • I J J I E ; , q |'d * ^d y

; (2)

-∞ -∞

-∞ -∞

γ = n2/(λ ⋅ a2), where Al,m is complex envelope of mode with the azimuthal l and radial m orders; αl,m is loss of mode with azimuthal l and radial m orders; β1l,m, β2l,m are inversed group velocity and dispersion parameter for mode with orders l and m; Cl,m;p,q is mode coupling coefficient between mode with orders l and m and mode with orders p and q; El,m is radial mode electric field distribution; n2 is nonlinear parameter corresponding to optical fiber material; λ is operating wavelength; a is optical fiber core radius;

During simulation we numerically solved system (1) by Split Step Fourier Method (SSFM) [20, 21, 26]. Gen-

erally this approach provides to find solution for piecewise regular transmission links under taking into account linear mode coupling. However, in the case of telecommunication fiber optic cables and optical fibers we supposed that linear mode coupling may be neglected. Proposed assumption allowed performing detailed comparison the influence of nonlinearity distortion factors during optical signal transmission by particular linearly polarized modes and their combinations.

During simulation, we utilized known models of DQPSK-system transmitter and receiver as well as model of Erbium doped fiber optic amplifier described in publication [27]. Also amplified spontaneous emission (ASE) was taken into account, and optical fiber loss complete compensation over transmission span was supposed. Dispersion was compensated by the equalizer placed at the regeneration span output, and its parameters were defined by preliminary performed test results. We estimated BitError-Ratio (BER) after equalizer signal processing according to recommendations based on algorithm described in work [27].

Computation of optical fiber mode staff parameters

During mode staff parameters computation we took into account that optical fiber is weakly guiding optical waveguide, that allowed to apply weakly guiding approximation concerned with linearly polarized mode representation [28] and utilize fast and simple Gaussian approximation method [29]. We propose to use modification of Gaussian approximation earlier developed for analysis of optical fibers with complicated refractive index profile [30]. Here characteristic equation for equivalent mode field radius is written in the following form:

N2

k ² A n i r i ² [ F m¹ ) ( x ) ] [ - C = 0.                   (3)

I i = 1                                       J

Mode propagation constant is calculated as follows:

в 2, m = k 2 П 22 —

b          (1 + m)!

^q q ! ( m — q ) ! ( I + q ) !’

^A n i = n i ^{— n} 2 _{+ 1} ^;

X = R ²/ R 1 2 m ;

where L ⁽ _p ^{l )} ( x ) is Laguerre polynomial; n i is refractive index of i -th layer; R = r / a is normalized radius; r is radial coordinate.

Mentioned above formulas become more simple for considered two-mode step-index optical fiber. Here propagation constant of the fundamental mode LP 01 is defined by well known analytical formula derived from (3) – (4) [29]:

P 0,1 = ^{k 2 n} 022 1 ^{1 +} -^7 a ^     ^R 0,1

Ro:i = —1—;

^0,1   2ln( V )

where V is normalized frequency of optical fiber.

For the second higher-order mode LP 11 we derived from formulas (3) and (4) both characteristic equation for equivalent mode field radius and expression for propagation constant, which have following form:

V ²

₂ exp R 1,1

1 R 1 ² ,1

— 2 = 0;

(                                              I

P 2,1 = k² n 0 ² —4,1 1 + R 121 + J2-1 . aR 1,1

Optical vortices are well represented by combination of linearly polarized modes [8, 14, 15]. Here we consider optical vortices with complex amplitude propagation over twomode optical fiber described by combination of linearly polarized mode LP11 components in the following form [31]:

^^^^^^s

^^^^^^e

m !

£k2An^ml) ( Xi )1 +

L i = 1                       J

C-J:

2 T?2 I ; a • R l , m J

^^^^^^s

cos(ф + п/2)1     ( пI

, x I•exp j ; sin (ф + п /2) J     V 2 )

(m + I — 1)! ,         m+ + I — 2)!

C = m (      ^ + ( m +I — 1)^-----^ +

(m — 1)!                 (m — 2)!

+ 2 1 -У i i + l — i)!; i = 0 i ^!

where

L F m ¹ ) ( x )^] = x l L L* — 1 ( ^x )^] exp (^{— x} ) ;

2 ⁿ             q±L + 1У !

^Ф( „ ⁾⁽ x ) = exp^{( —} x ) • £ g _q • x q + £ x ^{+ —} q = 0      L       k = 1 ( q + 1 — k ) !

q gq Z-l у q—j ;

j = 0

F¹ ( ^x 1,1 ) = x ¹ / ² • L¹ ( ^x 1,1 ) • exp ( ^{— x} 1,1 /² ) ;

^x 1,1 = ^R /^R 1,1 .

Results of fiber-optic link with two-mode fiber simulation

We performed simulation of 6000 km length long-haul fiber optic link with 100-km-per-span Erbium doped fiber optic amplifiers system. DP-DQPSK data transmission with 100 Gbps bit rate per channel is researched. Two-mode step-index optical fiber supporting propagation of two linearly polarized modes LP 01 and LP 11 was considered. It contains Germanium-doped fused silica core with radius 4.5 ц т bounded by solid outer fused silica cladding. Step refractive index profile height parameter is A = 0.025.

At first step we compared optical signal transmission by excited only one guided linearly polarized mode ( LP 01 or LP 11 ) supported by described fiber. Analogously to work [5] we supposed, that only one operating (or "active") mode is amplified. The next step was concerned with simulation of signal transmission by two linearly polarized modes and by optical vortices. Here we examined two version of receiving differing only by equalizer connection scheme.

All computed data were compared with simulations performed for the same fiber-optic link configuration but with standard single-mode optical fibers of ITU-T Rec. G.652. Sample of eye-diagram been computed during simulations is shown on Fig. 1. As a result of modeling we obtained curves of error probability dependence on transmitted optical channel power level. Optical channel potentiality was estimated analogously to work [5] as maximal possible value of power level providing still required quality of signal at the receiver end by using of error-correcting codes. According to work [32], forward error correction (FEC) DP-DQPSK system optical channel error probability boundary under described dispersion and nonlinearity factors corresponds to range 10–2…10–3. Here analogously to publication [5] we used probability error limit value equal to 3.8· 10–3. This threshold is further denoted in Fig. 2 – 4 as FEC limit

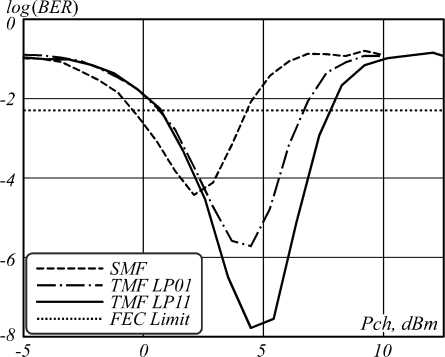
Fig. 2. Optical channel transferring by only one linearly polarized modes LP 01 or LP 11 supported by considered twomode optical fiber

Fig. 3 shows simulation results during optical channel transferring by two linearly polarized guided modes LP 01 and LP 11 over described above two-mode optical fiber. Here improvement for optical channel power level grows up to 5.25 dBm or 6.19 dBm in comparison with single mode fiber depending on receiver error correction method. Moreover it also increases up to 2.7 dBm or up to 3.8 dBm in comparison with previous case corresponding to optical channel transferring by only one linearly polarized mode LP 01 or LP 11 respectively.

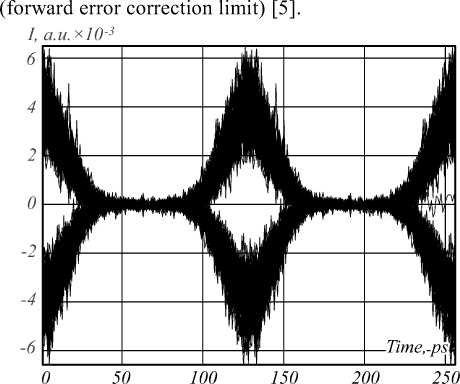
Fig. 1. Example of eye-diagram received at the equalizer output

Fig. 2 demonstrates results corresponding to modeling of optical signal transmission over described above two-mode optical fiber by one particular order linearly polarized mode LP 01 or LP 11 . Here due to using two-mode optical fiber it is able to increase optical channel power up to 2.37 dBm by transferring impulse by the fundamental mode LP 01 in comparison with standard single mode fibers ITU-T Rec. G.652, while it may be improved up to 3.48 dBm by optical channel operation at higher-order LP 11 guided mode. A good agreement should be noticed with researching results published in work [5] and experimental data represented in paper [9].

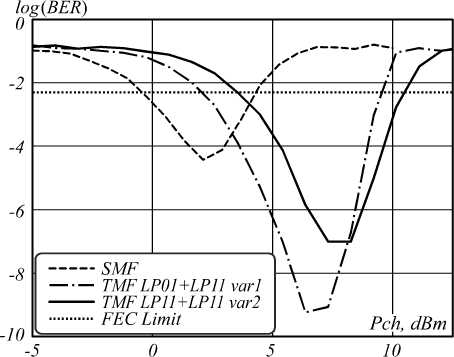
Fig. 3. Optical channel transferred by two linearly polarized modes LP 01 and LP 11 supported by considered two-mode optical fiber

Fig. 4 demonstrates simulation results corresponding to channel signal transmission by optical vortices over considered two-mode optical fiber. Here power level improves up to 5.14 dBm in comparison with single-mode optical fiber or e.g. up to the same value like in the previous case with optical pulse transferring by two linearly polarized modes LP 01 and LP 11 . Therefore optical cannel nonlinearity may be reduced by using combination of linearly polarized modes instead application of the only one linearly polarized mode with particular order for signal transferring.

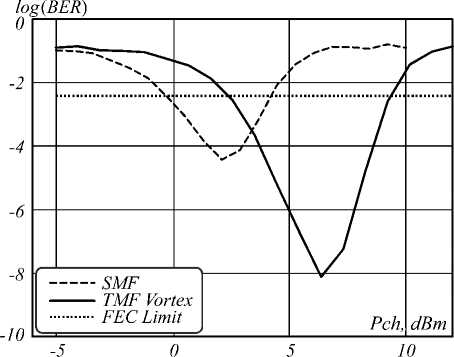
Fig. 4. Optical channel transferred by vortices over considered two-mode optical fiber

Conclusion

Presented results demonstrate advantages of fewmode optical fiber in comparison with single-mode in terms of nonlinearity distortion factors reducing for long-haul fiber optic links. We showed that for two-mode optical fiber the optical channel transmission by linearly polarized guided mode combination is more effective for nonlinearity decreasing in comparison with signal transferring by only one guided mode.