Simulation of algorithms for reducing the peak factor of OFDM signals and implementation of the best method for fading channgel

Data transmission with many subcarriers in the form of orthogonal frequency division multiplexing is widely recognized as one of the promising access schemes for use in developing wireless communication systems [1]. This data transmission mode is used in terrestrial television broadcasting in 4G and 5G generation communication systems, etc. [2]. The principle of OFDM operation is that high-speed data transmission is divided into many data transmission streams with lower speeds. Further, these streams arrive in parallel on orthogonal subchannels. Each subchannel can have its own type of modulator independently located such as BPSK, QPSK, QAM, etc. [3]. This versatility makes it possible to flexibly set the data transfer rate and effectively deal with selective fading and interference [4–7].

PAPR depends on the number of subcarriers of the considered signal, as well as on the modulation. The number of subcarriers is determined by the intended radio channel that will use the communication system. For channels with a strong effect of selective fading and significant intersymbol interference, the optimal number of subcarriers starts from 2048. An OFDM symbol with N = 2048 of subcarriers in use will have a maximum possible PAPR equals to10*log10 (N) = 33.3 dB for QPSK, and 10*log10 (2.6*N) = 37.3 dB for QAM -256 [8].

According to the definition of PAPR, P is a vector containing the power of all samples of some OFDM symbol, [W], Pav = sum (P)/length(P) is the average power of a given OFDM symbol, [W]. Then the peak factor of the considered OFDM symbol will be

PAPR = 10 log ( max^{{ p }} W],                      (1)

• V Pav j

where max{P} is a function that determines the largest value among the vector of values P.

In foreign and domestic literature, there are many algorithms for reducing the peak factor of OFDM signals, which make it possible to relax the requirements for the analog transmission and reception path. Such algorithms as Peak Cancelation Crest-Factor Reduction (PC-CFR), Partial Transmit Sequence (PTS), Selected Mapping (SLM), Discrete Fourier Transform spread OFDM (DFT-s-OFDM), Active Constellation Extension (ACE), Tone Reservation (TR) have been analyzed.

Direct clipping algorithms

Direct clipping algorithms [9; 10] (Peak Shrinking and Interpolation (PSI), Peak Cancelation CrestFactor Reduction (PC-CFR), Amplitude Clipping and Filtering) limit the signal to a certain level, leveling the consequences of this operation. They give an average PAPR reduction result. This is achieved at the cost of a significant deterioration in the bit error of the entire communication system as a whole. Out-of-band radiation appears, which has to be reduced by additional filtering, that adds the complexity to the implementation of this algorithm.

Partial Transmit Sequence Algorithm

The Partial Transmit Sequence algorithm (PTS) divides the input OFDM block into W subblocks, on which W of idependent IFFT operations (inverse fast Fourier transform) are performed, the results are multiplied by W of optimization coefficients and summed to each other.

The coefficients K 1 , K 2 ... K M have V of allowed values. These coefficients are calculated in such a way as to minimize PAPR of the output symbol. The block diagram of this method is shown in Fig. 1.

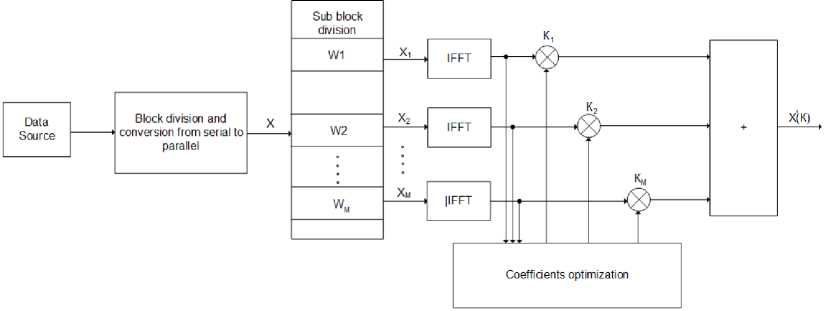
Рис. 1. Структурная схема PTS

Fig. 1. Block diagram of PTS

In the following, the PTS algorithm was simulated for different combinations of blocks W and V of allowed values of the coefficients. Fig. 2 shows the result of reducing PAPR depending on the CCDF (cumulative distribution function). It is shown that with an increase in the number of allowed values of the V coefficients, the efficiency of the algorithm increases. An increase in W blocks leads to an insignificant decrease in the peak factor. This algorithm requires additional processing at the receiver side and an additional channel for transmitting coefficient data to the receiver (log 2 (W^M-1)) bits per OFDM symbol. In summary, its performance is low, considering the computational complexity.

Selected Mapping Algorithm

The Selected Mapping algorithm (SLM) [11] is similar to PTS. The transmitter creates several potential OFDM data blocks, from which the block with the lowest PAPR is selected. Each block of data X is multiplied by U of different phase sequences B, each of length N, B(u) = [bu0, bu1, …, buN–1]T. IFFT is applied to the result, thus obtaining U of OFDM blocks x(1), x(2), ... x(U). As a result, among them, the block that has the smallest maximum value is selected. The effectiveness of PAPR reduction depends on the number of phase sequences, which also increases the number of IFFT blocks needed. Also in the classical implementation, an additional data channel is required to transmit the phase coefficients to the receiver. The complexity of the implementation rests on U of OBFT blocks.

Fig. 3 shows the results of the algorithm at U = 4 for an OFDM symbol with a QAM-256 data stream. It can be seen that the decrease in PAPR is about 2 dB. In summary, the performance of the algorithm is low when considering the computational complexity.

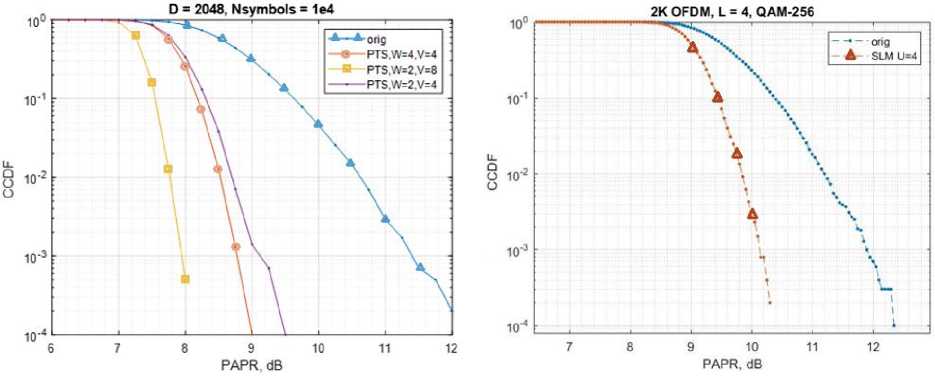
Рис. 2. Результат обработки OFDM сигнала алгоритмом PTS

Fig. 2. Result of OFDM signal processing by the PTS algorithm

Рис. 3. Результат обработки OFDM сигнала алгоритмом SLM

Fig. 3. The result of OFDM signal processing by the SLM algorithm

DFT-spread-OFDM Algorithm

The DFT-spread-OFDM approach is widely used in uplink signal transmission in the LTE (LongTerm Evolution) and 5G NR (SC-OFDMA) mobile communication standards [12]. The principle of operation of the algorithm is to precode subcarriers with data using FFT (Fast Fourier Transform) on the transmitter side before OFDM modulation. At the receiver side, after OFDM demodulation, the block is also decoded with an additional IFFT operation. The performance of the method does not depend on the modulation of the signal.

The performance of the DFT-spread-OFDM algorithm was evaluated on an LTE signal with QAM-4 modulation and a bandwidth of 20 MHz. The simulation results of the algorithm are plotted in Fig. 4. UL is the crest factor curve after the algorithm, DL is the signal without the algorithm, DL x8 is the signal with 8 times increased resolution.

Fig. 4 shows that the DFT-spread-OFDM algorithm reduces PAPR by 2.4 dB. In summary, the performance of the algorithm is average, with low computational complexity.

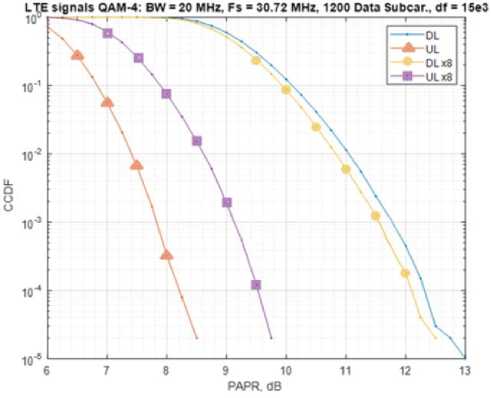
Риc. 4. Результат обработки OFDM сигнала методом DFT-spread-OFDM

Fig. 4. The result of OFDM signal processing by the DFT-spread-OFDM method

Tone Reservation Algorithm

The Tone Reservation (TR) algorithm is a very flexible method. Its performance strongly depends on the selected Reference kernel and the number of iterations. The work [13] describes in detail the process and approaches to designing a Reference kernel, as well as the TR algorithm itself.

Fig. 5 presents a block diagram of the TR algorithm [14], which shows that in the input OFDM block x , the maximum value modulo and its position (Peak detection) are searched, then a Circular shifting of the Reference kernel stored in memory is performed by the number of samples corresponding to the position of the maximum. Then the optimal coefficient is searched for in the Scale and phase rotating block, which is multiplied by the cyclically shifted Reference kernel, obtaining the signal C n . Further, the signal C n is added to the input OFDM signal X n , obtaining a block y with a reduced PAPR relative to X n .

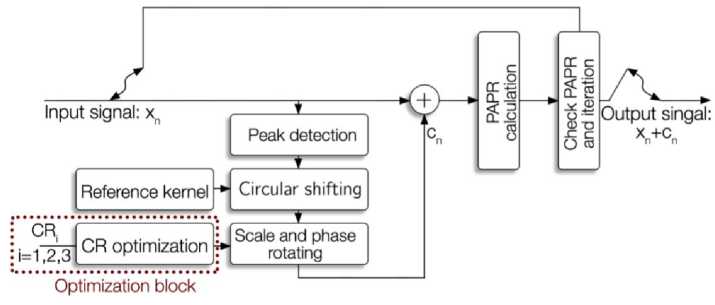
Рис. 5. Структурная схема алгоритма TR

Fig. 5. Block diagram of the TR algorithm

The advantages of the TR algorithm are as follows. It is economical on FPGA resources, does not distort the signal, is equally effective for all types of modulation (from QAM-4 to QAM-256) and does not require a reverse channel. But this algorithm has some disadvantages. It reduces the potential data rate, increases the average signal power, requires 10 iterations for high efficiency, slightly worsens the BER (due to the increase in the average signal power).

The efficiency of the TR algorithm was evaluated on a signal with QAM-16 modulation. The result of the algorithm is shown in Fig. 6.

The algorithm was modeled for 2048 subcarriers with 10 iterations, where a kernel block from the DVB-T2 standard was used. The percentage of TR subcarriers relative to all useful subcarriers is less than 5%, therefore, kernel blocks with a large number of TR subcarriers were considered (5, 10 and 20%) and with different number of iterations, as shown in Fig. 7.

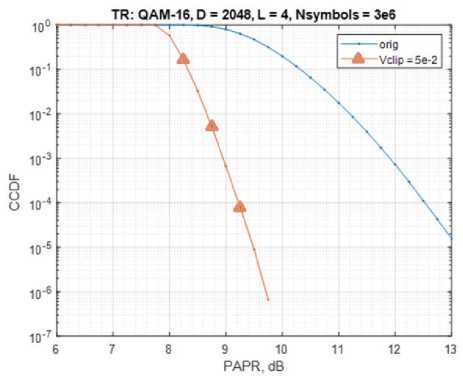
Рис. 6. Результат обработки OFDM сигнала алгоритмом TR (DVB-T2)

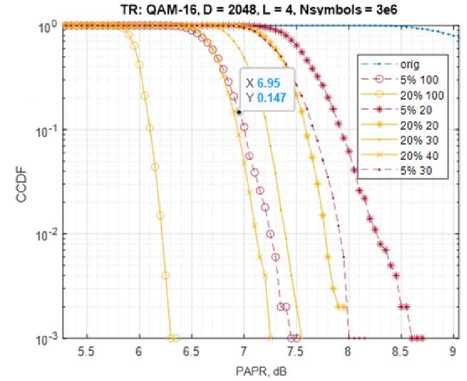
Рис. 7. Результат обработки OFDM сигнала алгоритмом TR

Fig. 6. Result of OFDM signal processing by TR algorithm (DVB-T2)

Fig. 7. Result of OFDM signal processing by the TR algorithm

The type of modulation does not affect the peak factor reduction in the TR algorithm, so there will be a similar gain for all constellations. It can be seen that the algorithm can give a reduction in PAPR from 3 dB (5% 10 iterations) to 5.8 dB (20% 100 iterations). In summary, TR has good performance at medium complexity.

Active Constellation Extension Algorithm

The Active Constellation Extension (ACE) algorithm uses the possibility of expanding the signal constellation on the sides without distorting the transmitted symbols [15]. Obviously, with an increase in the modulation order, the number of symbols that can be extended sideways will decrease relative to the total number of symbols, which will affect the performance of the algorithm. So, for QPSK, 100% of the symbols can be expanded sideways, and for QAM-16, only 75%.

A block diagram of the ACE algorithm, where the FFT and IFFT blocks perform the FFT and IFFT functions is shown in Fig. 8. The Clip block clips the signal in the time domain to a given level and the 4x-FFT operation moves the signal back to the frequency domain.

Between the received after clipping subcarriers X' and the original subcarriers X, the difference in the Cclip block is searched. This difference is a set of complex vectors with a random phase, then only those vectors are determined that point in the direction allowed for the corresponding subcarrier (symbol). This is done using filtering logic, resulting in signal C. Next, signal C is translated into vector c using 4 IFFTs (IFFT). Then, based on the maximum amplitude of the OFDM block and the projection of the vector c onto the original signal x, the balancing coefficient u is determined, which, together with c, is used to correct the input signal (y = x + u*c).

The advantages of the ACE algorithm are as follows. It does not affect the data transfer rate in any way, does not have a reverse channel, and does not distort the signal. The ACE algorithm has some disadvantages. Its efficiency decreases as the modulation order increases (from QAM-4 to QAM-256),it increases the average signal power, it is complex in hardware implementation (requires 3 FFT operations), worsens BER (due to an increase in average signal power).

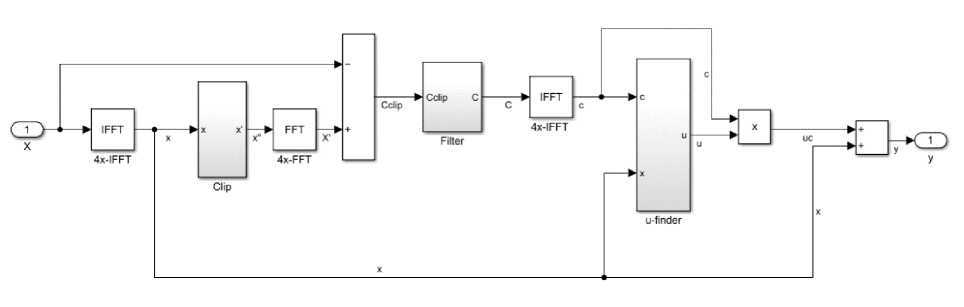
Рис. 8. Структурная схема алгоритма ACE

Fig. 8. Block diagram of the ACE algorithm

The results of ACE operation for a 4-QAM OFDM signal are shown in Fig. 9. After the first iteration (ace x1 curve) PAPR decreased by 4.4 dB, after the second iteration (ace x2 curve) by another 1.2 dB, and in total it decreases by 5.6 dB. In summary, ACE has good performance at medium complexity.

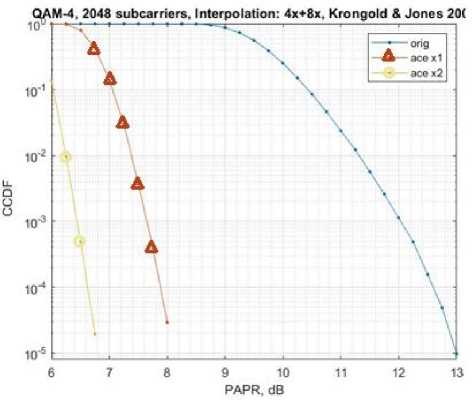
Рис. 9. Результат обработки OFDM сигнала алгоритмом ACE

Fig. 9. Result of OFDM signal processing by ACE algorithm

Combination of PAPR reduction algorithms

A combination of several peak factor reduction algorithms can produce greater peak factor reduction than either algorithm alone. So, it is possible to implement a combination of ACE and TR algorithms.

The block diagram of the combination block of PAPR reduction algorithms is shown in Fig. 10. In the proposed implementation, the ACE algorithm is first applied to the input signal, and then TR algorithm is applied. The ACE subsystem is presented in Fig. 11, PAPR subsystem is presented in Fig. 12.

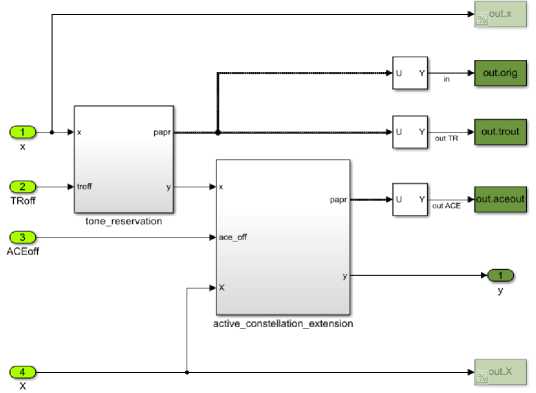
Рис. 10. Структурная схема комбинированной системы снижения пик-фактора

Fig. 10. Structural diagram of the combined PAPR reduction system

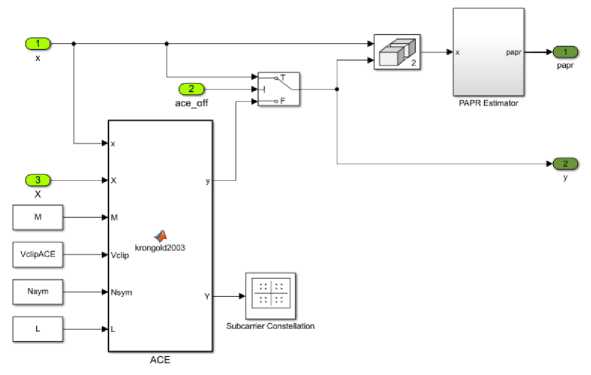
Рис. 11. Структурная схема подсистемы ACE

Fig. 11. Structural diagram of the ACE subsystem

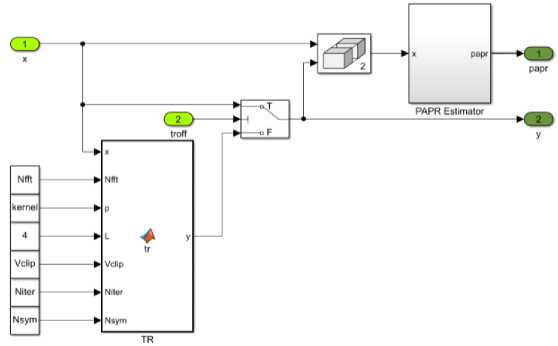
Рис. 12. Структурная схема подсистемы TR

Fig. 12. Structural diagram of the TR subsystem

The software implementation of the ACE algorithm is shown in Fig. 13; the software implementation of the TR algorithm is shown in Fig. 14.

15 1€

3€

4G

GO

G3

G4

function [yrY] = krongold2003 (x,X,M, Vclip,Nsym,NsymH, L) Nfft = 2048;

x = x*L;

X = X*L;

H SGP-ACE proc.

for j = l:Nsym if j <= NsymH extborder = 2;

else if M = 25€ I I M = 128 II M = €4 extborder = 4;

elseif M = 1G extborder = 2.82;

else extborder =2;

end end xl = x((j-1)*Nfft*L+l:j*Nfft*L); XL = fftshift(X((j-l)*Nfft*L+l:j*Nfft*L) ); %1) Starting with the data symbols in X ... avp = mean(abs(xl).*2); % Symbol average power % 2) Clip

A = sqrt (avp*10* (Vclip/10) ) ;% !! Convert clipping level (dB to V) xll - xl;

xlKabs(xl) > A) = A*exp (li* angle (xl (abs (xl) > A)));

% 3) Compute the clipped signal portion cclip = xll-xl;

% 4) FFT Cclip = fft(cclip)/sqrt(length(cclip));

% 5) Keep only extension with acceptable direction

Xl = XL+l*Cclip;

absRe = abs(real(XL));

abslm = abs(imag(XL));

reisext = absRe < abs(real(Xl)) & absRe >= extborder & abslm > 0; imisext = abslm < abs(imag(Xl)) & abslm >= extborder & abslm > 0;

Cre = zeros(Nfft*L,1);

Cim = zeros(Nfft*L,1);

Cre(reisext) = real(Cclip(reisext));

Cim (imisext) = imag(Cclip(imisext));

C = complex(Cre,Cim) ;

c = ifft(C)*sqrt(length(C));

% Determine a step size u

% 1’) Find max sample [E,nmax] = max(abs(xl)); % 2’) Compute projection of c cproj = real(xl.*conj(c))./abs(xl); % 3') Compute approx balancing u = (E-abs(xl(cproj > 0)))./(cproj(cproj > 0)-cproj(nmax)); % 4’) Find minimum u if isempty (u (u>0) ) mu =1;

else mu = min(u(u>0)); end % 6) Compute x[i+l] X((j-1)*Nfft*L+l:j*Nfft*L) = XL+mu*C; % For next iteration x((j-1)*Nfft*L+l:j*Nfft*L) = xl+mu*c; % Output end

Y = X*0.25;

y = x*0.25;

Рис. 13. Программная реализация алгоритма ACE

Fig. 13. Software implementation of the ACE algorithm

function у = tr(x,Nfft,p,L,Vclip, Niter, Nsym)

% Алгоритм TA for j = l:Nsym for i = 1:Niter

S

э

[yi, mi] = max(abs(x((j-1)*Nfft*L+l:j*Nfft*L))); % Search of maximum if yi <= Vclip break end kernel = [p (Nf ft*L-mi+2 :Nf f t*L) ; p(1:Nfft*L—mi+1)]; % Kernel-block shift alpha = x((j—1)*Nfft*L+mi)/yi*(yi—Vclip);            % Search for scale coef.

x((j-1)*Nfft*L+l:j*Nfft*L) = x((j-1)*Nfft*L+l:j*Nfft*L) - alpha*kernel; % Correct end end у = x;

Рис. 14. Программная реализация алгоритма TR

• Fig. 14.    Software implementation of the TR algorithm

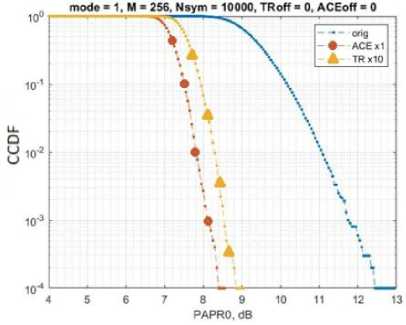
  The probability diagrams of exceeding PAPR are shown in Fig. 15 for 10000 OFDM symbols for basic modulations and all modes. These diagrams can also be referred to when considering the operation of the TR algorithm separately from ACE.

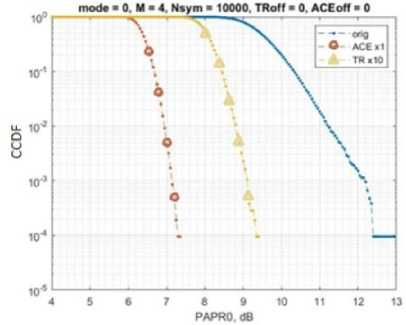
а

Рис. 15. Результат снижения пик-фактора алгоритмами ACE и TR: а – для QPSK; б – 256-QAM сигнала

б

• Fig. 15.    The result of reducing the crest factor by the ACE and TR algorithms: a – for QPSK; b – 256-QAM signal

Conclusion

The main methods for reducing the peak factor of OFDM signals, suitable for use in channels that are significantly affected by selective interference, intersymbol interference, and frequency-selective fading, are presented in this article.

The use of peak factor reduction algorithms can significantly reduce the requirements for the linearity of the transmitter amplifier of the communication system. The software implementation of the combined method of struggle in the Simulink software environment is given, which, in the future, will be implemented in a serial product. The combination of ACE and TR algorithms makes it possible to reduce the peak factor for OFDM signals by ~5.5 dB for BPSK data stream and ~4.5 dB for 8-PSK, QAM-16, QAM-64, QAM-128 and QAM-256 data streams, thereby improving the efficiency of the overall communication system.