Simulation of plastic deformations in metal rolling

Model of plastic deformations in rolling of porous materials

A real deformation state in a plastic zone beneath rolls and corresponding kinematic and dynamic conditions on the contact surface are considered as a limited one for the consequent approximate deformation states and found out by the method of approximated approach [1 – 5]. In this process the real values of the variation parameters describing the deformation state, kinematic and dynamic conditions on the contact surface are calculated by the step-by-step using of the basic energetic relationship of plasticity [6 – 11]:

• v . THav + ^ j J _n . T_s|Av_T| j dQ-

  -f_Fk^dF = 0 (1) and the variation inequality describing the principle of minimum of entire deformation energy [12 – 14]:

Jv TH^dV + Xj Jn.TsIAvTljd^ -

Lj^VdF>0. (2) where an asterisk marks is for the values relating to a kinematic admissible deformation state in the plastic zone; H – the intensity of the shear strain rates; T – the intensity of the shear strains (T = τs – in the state of ideal plasticity); p = [px; py; pz] - a vector of the surface unit pressure and its components; v = [vx; vy; vz} -a vector-velocity of a particle displacement in the deformation zone V; |AvT| j - a leap of the tangent component of a velocity on a discontinuous surface Ωj; Fk – the contact surface. In constructing the mathematical model of the rolling process the following assumptions are adopted:

• 1)    any plastic deformation state is described in accordance by the plane cross sections hypothesis [15], when

O x = O x to, V x = V x to, P x = P x (^); (3)

• 2)    an increasing of porous material density dρ on any cross-section x ∈ [0; l] of the plastic zone is proportional to a product of a relative degree of deformation dh / h ( x ) on this cross-section, of an accumulative logarithmic deformation ln( h 0 / h ( x ) ) and at the same time is inversely proportional to strip density at the same crosssection of the deformation zone, that is

dP = ^\l^^^» (4) where A is a proportional coefficient; m and n (m ≥ 1, n ≥ 2) are parameters characterizing the rate of porous strip compactness in the direction of rolling (Fig. 1).

S olv ing di f fe r ent ia l r elati onshi p ( 4 ) under the boundary conditions given:

p(x)\x=t = p0, p(x)\x=0 = p^         (5)

where x = l i s the equation of the e nt e r p la ne a n d x = 0 is the eq ua t i on of th e e x it p la n e o f th e d e for ma tion zone in r o ll ing r e spe ctiv e ly , i t i s f o und o ut the fol lowing a na ly ti c f unc t ion desc rib ing p o ro u s m at eri al d en si t y d i s tri b u t i o n al o n g th e p l astic deformation zone (Fig. 2): p^p » - /^/—1]{ -=5^ (6)

^p 0              ¹ПП о ^/? 1

• 3)    de ns ity of por ous s trip and a ny k ine ma tic - admissib le def or ma tio n state a re int e rr elate d by ac c o r ding to t he c on st a nt ma ss l a w whic h is written as follows

^div(p^ = £ ^(pvx) + ^p(%) [^ 7 ⁺ 5] = °, ⁽⁷⁾

where the assumptions mentioned above are taking into account;

• 4)    on the contact surface z = h ( x ) = R + h ^ —

—^R2 — %2,% G [°; Z], there is a relative movement and an intensive force vector of friction f is defined as following:

^f = fv⁽x⁾ !^^ _v

where f is a friction coefficient; p = p(x) is a function describing the changing of intensive normal pressure on the contact surface along the direction of rolling; is a velocity-vector of relative movement on the contact surface.

An initial deformation state is chosen as that concerning to rolling process without broadening. Using basic energetic relationship (1) adopted to an elementary volume as a thin cross-section layer of the deformation zone we have got a differential equation of the distribution of normal

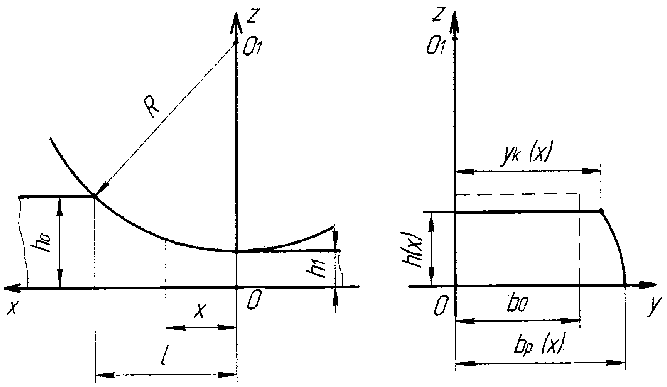
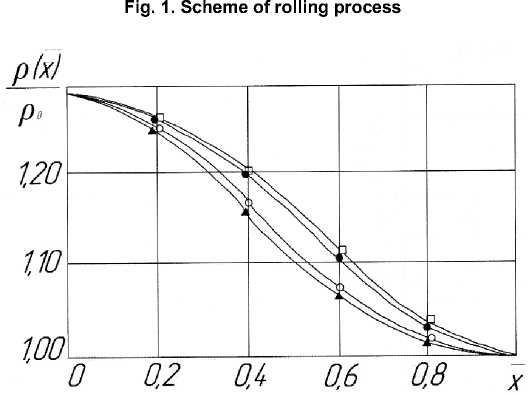
Fig. 2. Density curves of porous strip along the deformation zone (x = x/Z) when the ratio is —=1,29: • - m =1, n = 1; ▲ - m = 2, Po n = 2; □ – m = 1, n = 3; ○ – m = 2, n = 3

Обработка металлов давлением…

intensive pressure on the contact surface. Solving this equation with taking into account the characteristics of the initial deformation state there found out the corresponding dynamic ( p = p ( x )) and kinematic (a value of critical angle γ ) conditions on the contact surface. Then fixing on these dynamic and kinematic conditions on the base of variation inequality (2) there are found out characteristics of the first deformation approach state. Repeating the procedure mentioned above there are defined corresponding kinematic and dynamic conditions on the contact surface. Analogously there are calculated the following approaches of deformation states. An exit of this iteration process is done by means of reaching the accuracy given before for one of the important technologic parameters.

admissible velocity field in the deformation zone beneath rolls:

^V x ^(x) = p(X5 ^V i [ 555 ] ‘ ^;

^V y ^(x,^y,^{z) = -} Pⁱ)1+i^XX;:) ^y dX ⁽P^V x ^{);    (12)}

^ V z ⁽X,Z) = -

1 d p(x) dx du

where 9 = f¹             .

J0 i+a0+a1u+a2u

^{z d}

⁽^^{V x )}J o i+k(x,t) ’

2 "

Relying on the values and relationship of the variation coefficients a 0 , a 1 , a 2 and the variation parameters n, m, ρ 1 in formula (6) the different variants of kinematic admissible states in the plastic deformation zone are constructed.

Kinematically admissible trajectories of particles displacement in the deformation zone

A kinematically admissible velocity field in the deformation zone

Let's consider the deformation zone in rolling of porous strip with a rectangular crosssection area in two rolls when a changing of broadening is not uniform along a height of rolling porous strip. Due to symmetry of plastic flow along the height and width of the deformation zone the analytic describing of the rolling process is considered for 1/4 part of the deformation zone (Fig. 1). A kinematically admissible velocity field and corresponding deformation state of plastic zone are constructed on the assumptions mentioned above and the following addition hypotheses:

• 5)    there is a relative movement of material particles on the contact surface:

V n = V_x⁽x⁾ ^ - V z [x, y, ^⁽x^)] = 0;     (9)

• 6)    there are the kinematic conditions on symmetric planes:

As is known on the base of functions (12)

and the differential equations of trajectories,

namely dy _ yy(x,y,z) _ dz _ vZ(x,z) dx     ^x(x) ; dx vx(x) ,

where x is an independent variable, we are able to calculate on any computer by means of one of numerical methods the kinematically admissible trajectories of particles displacement in the plastic

deformation zone in rolling. Let’s point out two simple partial cases of solving of system (13).

SOLUTION 1. Let’s find out trajectories of particles displacement on the horizontal symmetry plane z = 0. At this case differential system of equations (13) is transformed as follows:

dy dx

-

—"(№); ?=0.

1+a0pvxdx    x dx

V y (x, 0, z) = 0; v_z(x, y, 0) = 0;

7) the components ξ y and ξ z of the deformation rates at any point of the plastic zone are interrelated as follows:

Integrating of system (14) gives the following equations of trajectories on the plane z = 0:

«0

y(x) = y o [ ^pP^x)^ ^ (^x2 ] ^1+ao;z(x) = 0, (15) where y 0 is an у -coordination of a particle on the enter cross-section plane x = 1.

= k(x,z,a₀,a₁,a₂), 5 Z where

k(x, z, a o ,a i , a₂) = « o + « i ^x_ + « 2

SOLUTION 2. Let’s find out trajectories of particles on the contact surface z = h ( x ). Reasoning analogously, we have got the following equations:

z² h²(x) ,

a 0 , a 1 , a 2 – the variation coefficients the real values of which are found out as the result of solving the general variation problem of plasticity. Taking into account all of assumptions and hypotheses mentioned above it is found out the following functions describing the kinematically

В

y⁽x) = y o [ ^^ ]^е; z⁽x) = h⁽x) ,       (16)

where _s = ^0 +0 1 +0^ .

1+a0+a1+a2

Analyses of the kinematically admissible model of particles displacement shows that the values of variation coefficients and parameters and as well their relationship give the following two cases on the contact surface:

• 1)    there is plastic flow along the Y -axis if

a 0 + a 1 + a 2 ≠ 0;

• 2)    there is no plastic flow along the Y -axis if a 0 + а 1 + a 2 = 0.

Results

• 1.    It is propounded a new hypothesis of density distribution of porous strip along the plastic zone in rolling and it is got corresponding analytic function.

• 2.    In case of simple rolling process, it is constructed spatial kinematically admissible velocity field (12) that is not uniform along the height (the Z -axis) and the width (the Y -axis) of the plastic deformation zone.

• 3.    It is worked out the method of approxi-

• mated approaches inside of which the basic energetic relationship of plasticity (1) and the variation inequality (2) expressing the principle of minimum of entire deformation energy are interrelated.

The work was supported by Government of the Russian Federation (Act 211, contract No 02.A03.21.0011) and by the Ministry of Education and Science of the Russian Federation (4.5749.2017/7.8). The paper was written with support from the Ministry of Education and Science of the Russian Federation in the framework of the project “Development of new methods and technologies to create products for electrical and structural application of graphitic composite materials by means of high-speed dynamic molding” of the State task No 9.1329.2017/4.6.