Simulation of the evolution of laser beams in impurity carbon nanotubes using the Madelung approach

One of the main tasks of nonlinear optics is the study of the interaction of high-power laser radiation with various media. Recently, many works have been devoted to this topic, including the field of theoretical modeling [1 – 3], which allows not only to identify new interesting effects, but also to find the media most suitable for obtaining or maintaining specified radiation parameters. Note that carbon nanotubes (CNTs) are promising from the point of view of stable propagation of the electromagnetic field [4]. They are widely used in many nonlinear optical applications [5], including the creation of fiber [6] and soliton laser [7], generation of light pulses of various ranges [8], in the development of photonic devices, including optical memory [9], etc.

Another direction for using carbon nanotubes is the creation of waveguides based on them in view of the possibility of propagating localized structures, including light bullets [10]. At the same time, the influence of the parameters of a medium with nanostructures, as well as physical factors (external fields, nonlinear and multiphoton absorption) on the dynamics of electromagnetic radiation is studied. All this allows us to obtain a well-developed theoretical basis for the creation of modern information transmission systems. Thus, the work [11] shows the possibility of controlling the shape of an ultrashort optical pulse and stabilizing it by changing the amplitude of the pump pulse. Features of the pulse evolution in the presence of an external electric field [12] and magnetic field [13] have been revealed, as well as taking into account various absorption mechanisms. Note that the listed results were obtained without using the approximation of slow amplitudes and phases based on the Maxwell’s equations.

It is known, that the propagation of powerful electromagnetic radiation in a nonlinear medium can also be described using a different approach, using the nonlinear Schrödinger equation (NLS). In this case, the Madelung transformation connects Schrödinger-type equations in quantum mechanics and the Euler equations for liquids. Since 1927, when this transformation was proposed [14], many of its modifications have appeared, which are a useful approach in many applications: from stochastic mechanics to quantum cosmology [15 – 17]. We also note that the use of this transformation make it possible to apply and develop new numerical methods for effective modeling of nonlinear hydrodynamics [18], including more complex modifications of the problem of the dynamics of laser beams in various nonlinear media.

In this work, for the first time, we propose a model that describes the interaction of a laser beam with an array of impurity carbon nanotubes within the framework of the hydrodynamic approach.

Model and description of the research method

Let us consider the propagation of an electromagnetic beam in an array of zigzag single-walled carbon nanotubes, over which the impurity is uniformly distributed. The wave vector is perpendicular to the array and the OZ axis. In our model, all CNTs are parallel to the OX axis and are considered infinite.

The energy spectrum of electrons in impurity CNTs can be written in the form [19]:

& imp ( P x , S ) = 0.5 ^X ( R + Q +

+ /R - Q ) 2 - 4 ( D ■ ( f + f * )-< P x , s ) 2 - D 2 ) ] ^, (1)

where values R, Q determine the energy of electron transitions from impurity levels to each of the two sublattices of the nanotube, value D corresponds to the energy of electron transition, due to the presence of an impurity, from one CNT sublattice to another, f is the complex function that determines the electronic energy spectrum of CNT - e ( p x , s ) = | f | is the dispersion law for conduction electrons of CNTs in the absence of impurities [20]:

kB is the Boltzmann constant, T is the temperature, as,q = a | emp (Px,s)-cos (Px - a - q)-dPx.           (7)

^п BZ

Taking into account the expressions for the coefficients b s, q , a s, q , as well as the current densities, Eq. (3), describing the evolution of the field in an array of carbon nanotubes with impurities takes the following form:

e у Px , si Y 0 л i ± । cos I apx I cos        i । cos , mm

I                            I apx I      I ^s I I j + j = 2y01 cos (apx) + 2cos II cos I — II,

I                  I 2 J    I m JJ ea Id2 A a2 AI eaed2 A

1                   +I c к ay2 az2 J c3 at2

” m

-й2 ZZ bs. q sin q =1 s=1

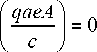
here s describes the quantization of a quasi-momentum along the perimeter of the nanotube cross section with the type ( m , 0), p x is the projection of the conduction electron quasi-momentum onto the CNT axis, y ₀ ® 2.7 eV, a = 3 b / 2h, b = 1.4-10 ^{- 10} m is the bond length between carbon atoms.

According to the studies carried out, the contribution of the level to the parameters of the impurity decreases with increasing the level number. Therefore, when considering impurity, we take into account only four levels [19].

The electric field of the laser beam has the form: E = ( E ( y , z , t ), 0, 0), electric current density is j = ( j ( y , z , t ), 0, 0).

The equation describing the behavior of the component of the vector potential of the electric field directed along the OX axis has the following form:

e d ² A d ² A a ² A 4п ,

=++ j ( A ) , c ² a t ² a y ² a z ²

ю0 is the characteristic frequency.

Next, let us non-dimensionalize the x -components of the vector potential:

ea

A = —A = A₀ ( y , z ) cos ( й t - kz - ф ) ,

A ( y , z ) is the envelope of the projection of the vector potential onto the Ox axis, k = й/е/ c is the wave vector module, ф is the initial phase.

Next, we use the Jacobi-Anger expansion for the function of the form sin(p-cos(c)) in formula (8). In the approximation of the slowly varying amplitudes and phases [22], as well as taking into account the formula for the Bessel function of integer order and its expansion, we obtain the equation for describing the dynamics of the amplitude of the vector potential: V ( y , z ) = A ( y , z ) exp ( i ф ) :

here c ® 3 - 10 8 m/ s, e is the dielectric constant of the medium. Field inhomogeneities along the CNT axis are not considered.

Next, we write the standard expression for the x -component of current density [21]:

m j = 2eZfu(Px,s)-F-dPx ,                      (4)

^s =1 BZ

a ² v ,. 5y --+ 2 1 к—

a^ ²

дт

-

m ”

-V ZZ b s , q Z q =1 s =1         r =0

( - 1 ) q ² r +¹ M ² r

2 ^{2 r + 1} r ( r + 1 ) Г ( r + 2 )

= 0

where e is the electron charge, u ( p_x , s ) = de _imp / a p_x is the electron speed, F is the Fermi-Dirac distribution function,, BZ is the first Brillouin zone.

Using the Fourier series expansion of the dispersion law, as well as the collisionless approximation, we can rewrite formula (4) in the form:

I qaeA I j =-en0Y0aZZbs■ ^s™ II, (5) q=1 s=1 к c J

here Г( r ) - gamma function, к = kc ² /й 0 , ^ = y й ₀ / c , т = z й₀ / c .

Next, we use Madelung’s approach [23] and rewrite equation (10) in the hydrodynamic form:

a

Р т + — ( p u ) = 0, at

кZ X

I a I        1 a uT + u~ u = 7_(P + pmp) ,

I at J     paJ

here n 0 determines electron concentration,

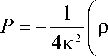
Р

b s , q

f ¹ v“ s ■ q c^os ( qr )L I cos ( qr ) exp I - Z           I dr

-п              к q =1      k B T     J

п

I exp

-п

Ю

-Z

q =1

cos ( qr ) k B T

, (6)

dr

1   ” m ”

P mP = ЙТ ZZZ ^{2 K} q =1 s =1 r =0

b s , _q ( - 1 ) r r q ^{2 r + 1} Р ^{r + 1}

2 ^{2 r + 1} ( r + 1 ) Г ( r + 1 ) Г ( r + 2 )

here p=M2, u =к^-1 дф/д^, P is the analogue of quantum pressure, P imp is the term determined by the nonlinearity associated with impurity carbon nanotubes.

Numerical simulation and results

We solve the resulting equations (11), using the method of smoothed particles (SPH - Smoothed-particle hydrodynamics) [24, 25], which has proven itself in solving problems of hydro- and gas dynamics and is being actively developed. Note that the SPH method is stable and does not lead to divergences. There are other numerical methods for solving the NLS equation, one of which is the split-step method [26, 27]. It is efficient and quite fast, but depends on the distribution of computational grid points. Mesh independence allows the SPH method to easily adapt to the specifics of the solution. Since the particles themselves are carriers of information about the state of the medium, regions of increased density are regions of increased numerical resolution. Also, the advantages of the SPH method include the simplicity of its algorithmic implementation and the ability to easily improve the model by taking into account additional physical processes. The computational complexity of both methods is O ( N -log N). Both methods perform well in solving NLS equations, including in combined form [28].

In SPH method, any physical quantity B ( r ) is specified in the form:

B ( r ) = E mA ( r j ) W ( r - r j , h ) • j Pj

The initial condition for the amplitude of the vector potential has the form:

y ( g ,0 ) = a о exp ( ^- q ² II f)

a о is the beam electric field amplitude and l z is the halfwidth of the beam at the initial moment of time.

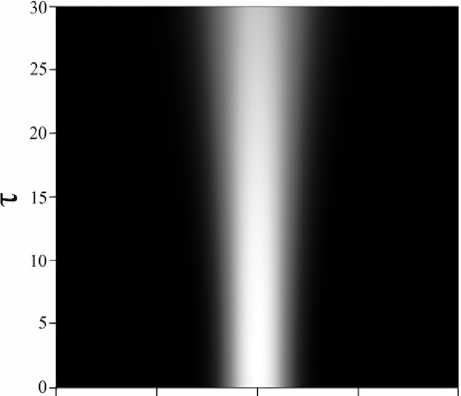
The dependence of the intensity of the electromagnetic beam (proportional to the value of p) on the coordinates during its propagation in a medium with carbon nanotubes without taking into account the impurity is shown in Fig. 1.

0            5            10           15           20

0.0       0.2       0.4       0.6       0.8      1.0

р/Ы2

Fig. 1. Laser beam intensity distribution in a CNT array

Let`s now study the influence of the impurity contained in the CNT array on the spatial-energy characteristics of the laser beam (Fig. 2 and Fig. 3).

We suppose that the parameter characterizing the change in electron energy during transitions between two nanotube sublattices caused by the presence of an impurity lies within the following limits: D e [0, y o ]-Taking into account the equivalence of CNT sublattices, we assume that the parameters R and Q are also equivalent. Therefore, the relation holds: R = Q =– D .

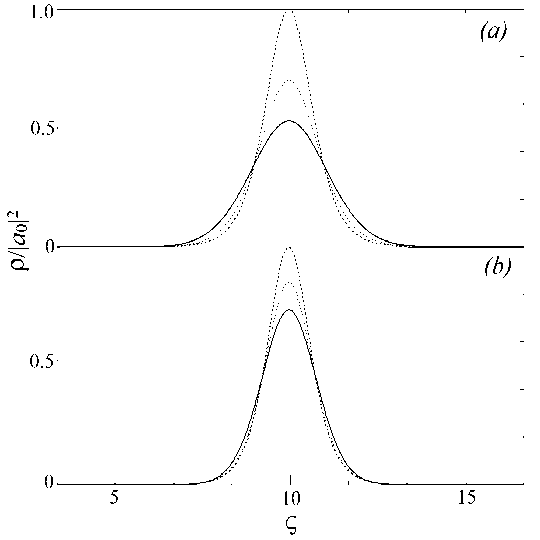
Fig. 2. Dependence of the laser beam intensity on the transverse coordinate ς at fixed values of the coordinate τ: the curves in figure (a) correspond to τ = 30 units, the curves in figure (b) – τ = 15 units.

The solid line – the absence of the impurity; the dotted line –

R = Q = – D = – 0.5γ 0 ; the dashed line – R = Q = – D = – γ 0

From Figure 2 it can be seen, that the behavior of the pulse does not change with increasing coordinate т for different impurity parameters; a narrowing of the laser beam is observed. Moreover, its intensity increases with increasing energy of impurity-mediated transitions. Note that by varying the parameters of the impurity, it is possible to increase its intensity by 50%. This behavior can be explained by a stronger connection between carbon atoms and impurities (with increasing impurity parameters), which leads to the change in the energy spectrum, and, as a consequence, the nonlinear properties of the medium, which ensure the ability of the beam to resist diffraction.

The influence of impurity on the laser beam width is shown in Figure 3. The width l corresponds to the distance at which the beam amplitude drops by a factor of 2.

Figure 3 demonstrates that the introduction of a dopant prevents the broadening of a Gaussian laser beam. In the absence of an impurity, the final width (at т=30) is approximately 1.5 times larger than for the impurity case.

Conclusion

• 1.    An analogue of the hydrodynamic equations is obtained to describe and simulate the propagation of the laser beam in an array of carbon nanotubes, taking into account impurities. This model allows us solving more complex problems taking into account additional effects, as well as generalization to the threedimensional case.

• 2.    It has been shown that, despite diffraction spreading, the laser beam in an array of nanotubes propagates over a considerable distance, which allows one to judge its stability.

• 3.    By varying the parameters of the impurity, we can control both the width of the laser beam and its intensity. Moreover, the presence of an impurity counteracts the spreading of the electromagnetic beam.

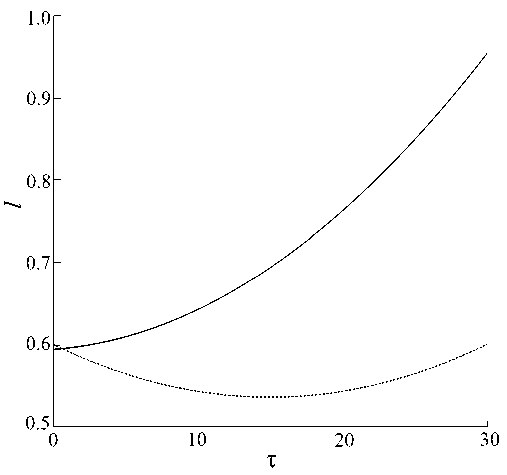
Fig. 3. Dependence of the laser beam width l on the running coordinate τ: the solid line – the absence of the impurity; the dashed line – R = Q = – D = – γ 0

Acknowledgments

The study was supported by the Russian Science Foundation (RSF) (grant no. 23-71-00016, . The work was carried out using the equipment of the Center for Collective Use of Ultra-High-Performance Computing Resources of Moscow State University named after M.V. Lomonosov.