Simulation of the magnetic structure upon ordering eg orbitals to the quasi-one- and quasi-two-dimensional magnets by quantum Monte Carlo method

Magnetic materials with double orbital quasidegeneration are characterized not only by spin-dependent interactions, but also by the dependence of the exchange integral on the mutual position of the orbitals. The interplay of spins with the charge-orbital ordering changes not only magnetic properties, but also transport characteristics, for example, gives rise to giant magnetoresistance in manganites. The orbital ordering forms a quasi-low-dimensional structure in KCuF3 [1] and two-dimensional antiferromagnetic in NH4CuCl3 [2] at low temperatures.

When studying the ground state and low-temperature effects in low-dimensional systems, one should remember that the quantum fluctuations in a spin system are of significant importance and, in the case of the strong interaction of spins with orbitals through the exchange interaction, it must be taken into account that the hopping integrals between the neighboring 3 d ions depends on both the orbital type and on the mutual position of the sites, because the electron-density distribution is not spherically symmetric.

The interrelation between the spin order and orbital ordering is clearly illustrated in a Kugel’–Khomsky model [1] for the Hamiltonian of perovskites ( e_g ions at the sites of a simple cubic lattice), which is obtained from the multielectron Hamiltonian with the same exchange parameters J = 4 t ² / U , where t is the hopping integral and U is the Coulomb-repulsion parameter at the site between the d_{z 2} – d_{z 2} and d_{x 2 – y 2}– d_{x 2 – y 2} orbitals.

The physical origin of this peculiar situation is the strong spatial anisotropy of the e_g orbital wave functions. This type of the orbital ordering provides the largest energy gain due to the quantum spin fluctuations. An orbital flip modulates strength of the neighboring exchange bond and causes the existence of the strong antiferromagnetic exchange interaction directed along the overlap of the orbitals with strong space anisotropy of the exchange interactions that are typical of the quasi-one-dimensional system under the condition of the presence of a gap in an orbital excitation spectrum.

In addition to the ferro- and antiferromagnetic ordering of the d _{3 z 2-– r 2} orbitals, the ordering of the d _{3 z 2 – r 2} and d_{x 2 – y 2} orbitals is also possible with account for the fact that the hopping integral between these orbitals may substantially differ due to the strong electron correlations. Strength of the antiferromagnetic interaction is determined by a region of the overlap of the 2 p– 3 d orbitals and depends on the orbital e_g state of an electron. The overlap integral between the d_{x 2 – y 2} and p_x orbitals is E_{x a} ( l , m , n ) = V 3/2 l ( l ² - m ² )( pd s), where ( pd s) is the overlap ^, integral between the d and p orbitals and ( l , m , n ) is the unit vector along the direction from a cation to an anion. The overlap integral between d _{2 x 2 – z 2 – y 2} and p_x orbitals is expressed as E_{x p} ( l , m , n ) = l [ n ² - ( l ² +m ² )/2]( pd s) [3]. Then, the hopping amplitude between adjacent copper ions via the p orbital along the x axis is evaluated as t _α ^x _β = E_x , _a (1, 0, 0) E_x(- 1, 0, 0) / ( e_p - e d ) [3], where e_p and e d are the energy levels for the d and p orbitals, respectively, and E_{x a} and E_{x p} are the overlap integrals of the d_{x 2} _ y ₂ and p_x orbitals and p_x ^, and d _{2 x 2 – z 2 – y 2} orbitals, which will be denoted as d_x ² .

The account for the Coulomb interaction between electrons located both at a site and between different orbitals will also lead to modification of exchange parameters and alteration of the Jaa IJpp relation between them. Below we consider a model with one electron (hole) on the eg orbital with an exchange interaction between them specified by a parameter. This model is applicable to perovskites containing Mn3+, Ni3+, Cu2+ and Fe2+ ions in octahedral environment.

This study is aimed to determination of the effect of the exchange interaction between e_g electrons on the ordering of d _{2 x 2 – z 2 – y 2} and d_{x 2 – y 2} orbitals in a Mott insulator and estimation of a region of the parameters, at which the magnetic order dimensionality changes from quasi-two-dimensional to quasi-one-dimensional antiferromagnetic. It is known that low-dimensional systems with alternating exchange imitating the spin Peierls transition are in a more stable state and have an energy gain of E I J ~ 5 , where 5 = J ₊₁ - J i _{+1 i +1}. The interaction of the electrons on the e_g orbitals with various octahedron oscillation modes forms orbital ordering. The most widespread type of the orbital ordering is associated with the alternating of the d _{3 x 2 – r 2} and d _{3 y 2 – r 2} orbitals whose schematic arrangement has the form b^b^ . The exchange altenating in the spin Peierls quasi-two-dimensional antiferromagnetic gives rise to dissappearing long range order and to the formation of a singlet state. Possible the alteration of exchange along of one direction of lattice as a result of orbital ordering causes the instability AF order.

Let us determine change of the magnetic properties and the magnetic order type at the formation of orbital ordering.

1D Model. Let us consider the quasi-one-dimensional models with the symmetric alternating exchange (fig. 1, b ) described by the Hamiltonian:

H -z[( J+6) SiS+1 +JS+iSi+2 + i ^)      ^)              ^)      ^)

+ ( J - 6 ) S i+ 2 S i+ 3 + JS i+ 3 S i+ 4 ] - I H i S i , and with the asymmetric alternating exchan ⁱ ge(fig. 1, c ):

H = -Z[( J+26) SiS+1 +JSi+1 Si+2 + i                                                   (2)

+ ( J - 6 ) S i+ 2 S i+ 3 +JS i+ 3 S i+ 4 ] - I H i S i .

2i where J ~ tα,β is the exchange interactions between electrons located at the nearest d3z2 – d3z2, dx2 – y2 – dx2 – y2 d3z2 – dx2 – y2 orbitals, there are J(1 ± 5), J(1 + 25), J(J < 0), 5 - a value of the alternating exchange; H is the external magnetic field. When the ratio of the hopping integrals is written as taa 11pp = 3/4 and tap 11pp = ^3/2 , the exchange interactions between electrons on the dx2 – y2 and d3z2 orbitals differ by a factor of almost: Jaa1J№ = 0.56, Jap1JPP = 0'75'

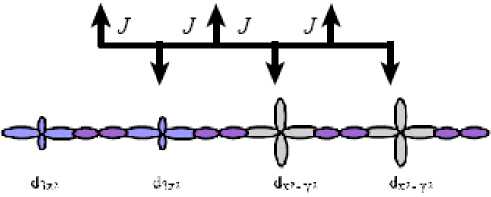
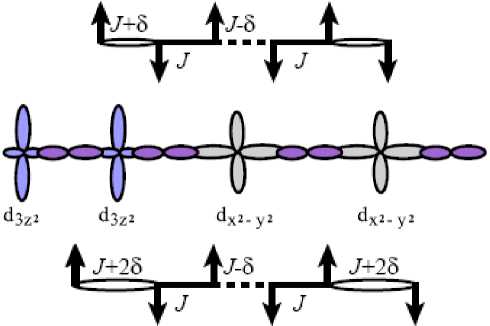
Fig. 1. Illustration of the orbital ordering d _{3 z 2} and d _{x 2 – y 2} for Neel AFM with homogeneous distribution of an exchange interaction ( a ), with the symmetric alternating exchange (eq. (1)) ( b ) and with the asymmetric alternating exchange (eq. (2)) ( c ) on a chain

As a calculation method, we take the quantum Monte Carlo method unifying two algorithms, worldlines and continuous time [4]. The continuous time world-line Monte Carlo approach is based on expansion of a statistical evolution operator exp(–H/T) by exchange interaction strength. The world-line configuration of spins flips under the action of operators of the creation and annihilation of a spin state in imaginary time and real space [4; 5]. For the spins S = 1/2 located at the sites of the chain L = 400 with the nonuniform exchange distribution and periodic boundary conditions in the Trotter direction and on the chain are used. The calculation method was described in detail in [6]. The following quantities are calculated in the framework of this method: the magnetization m = 2< S z >, spin-spin correlation function < S z(0)S z(r) >, correlation radius, static susceptibility c = m/H in the external magnetic field directed along the quantization axis, staggered magnetization ms, energy E, a magnetic structure factor

S ( q ) = ¹ ∑ exp( - iqr j ) S^z (0) S^z ( r j ). (3) N ^r j

The exchange alternating in the spin Peierls chain induces a gap in the spectrum of the triplet excitations and gives rise to a finite correlation radius in the ground state. Using the calculated dependences of the magnetization and spin correlation functions on the external magnetic field, we determine the critical fields H_c corresponding to the formation of the long-range magnetic order and the gap in the tripletexcitation spectrum. The calculations provide a linear dependence of ∆ ≈ 2 δ the gap on the exchange alternating and are in good agreement with the limiting case for one dimer, H_c = gS^zJ (1 + δ ) = 2 J . The thermodynamic characteristics – the specific heat and susceptibility -decrease according to the exponential law below this temperature.

The ordered arrangement of the orbital pairs described by Hamiltonian (eq. (2)) gives rise to the appearance of the plateau m = 1/2 on the magnetization curve m ( H ) at a critical external field H_{c 1} as shown in fig. 2, a . The magnetic structure factor determined from the spin-spin correlation function has the main maximum and a number of satellites. The magnetic field aligns the spins of the kinks along the field and stabilizes the long-range ferromagnetic order, which does not coincide with the shortrange order calculated by chain-averaging of the spin-spin correlation function in the first coordination sphere (fig. 2, b ). As the magnetic field increases, the modulation of the magnetic structure with the wave vector q = π /2 is observed near the magnetic field H ~ H_{c 1}. The arrangement of the spins in the chain in the plateau region H_{c 1}<  H <  H_{c 2}can be represented as ↑↑↑↓↑↑↑↓ . The linear dependence m ( H ) for low external fields (see fig. 2, a ) indicates the absence of the gap in the spectrum of triplet spin excitations and the magnetic state is a quantum spin liquid with the finite correlation radius.

The ordering of orbital pairs in the magnetic field provides three types of the magnetic order: short-range antiferromagnetic order, ferromagnetic order, and modulated ferromagnetic order with the wave vector is equal to Q = π /2, depending on the relation of the magnetic field and exchange alternating. Figure 3 shows the regions of these phases in the (magnetic field, exchange alternating) plane.

The decrease in the energy of the antiferromagnetic chain with the nonuniform periodic distribution of exchange is caused by the decrease in the effective chain length owing to a change in the correlation radius. In particular, in the limiting cases, the energies per spin in the infinite antiferromagnetic chain and dimer are E _chain = –2ln 2 + 0.5 ≈ ≈ – 0.443 3 J and E_d = –0.75 J , respectively. As a result, the energy of the alternating chain depends on the wave vector of the exchange modulation; i. e., the larger the number of the spins coupled by the strong exchange, the lower the change in the energy of the chain after the exchange alternating. The unit cell contains two and four spins in a spin Peierls magnet and in a magnet with orbital ordering, respectively. Figure 4 shows the Monte Carlo calculations of the relative energy change as a function of the exchangealternating magnitude.

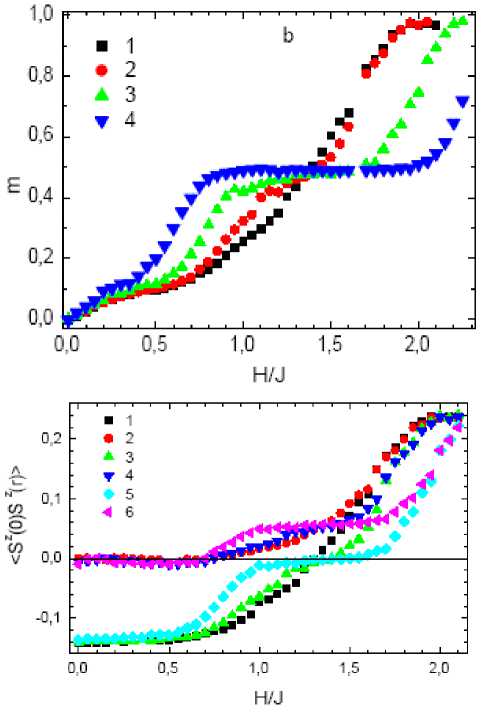
Fig. 2. Field dependences of the magnetization m ( a ) and spin– spin correlation functions < S ^z (0) S ^z ( r )> ?( b ) at the distance r = 1 (1, 3, 5) and r = 31 (2, 4, 6) for δ = 0.2 (1), 0.4 (2), and 0.6 (3). The symbol sizes correspond to the errors

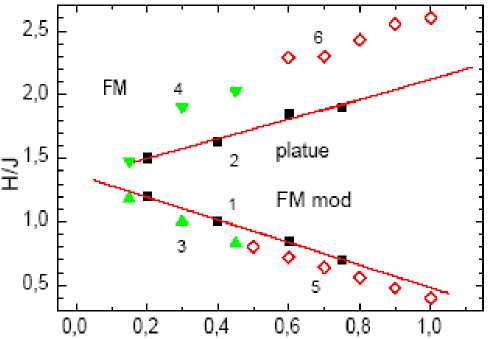
Fig. 3. Phase diagram of the magnet with the orbital ordering of pairs containing the regions with the short-range antiferromagnetic order (AF), ferromagnetic order (FM), and modulated ferromagnetic order (FM mod) with the plateau m ( H ) = 1/2 in the field region H _{c 1} (1) – H _{c 2} (2) in the (magnetic field, exchange alternating) plane. For the model with the symmetric alternating exchange (eq. (1)) are the critical fields H _{c 1} (1, 2), and asymmetric alternating exchange (eq. (2)) are H _{c 1} (3, 4, 5, 6). The critical fields H _{c 1} (5, 6) correspond to the singlet-triplet transition in a four-spin cluster and are calculated with δ → 1 by exact diagonalization method in this cluster

Using the typical parameters of the hopping integrals from the cation to anion t_{dz 2 – p} = 2 eV, t_{dx 2 – p} = 0.5 eV, and t_{d ( x 2 – y 2) – p} = 1.5 eV, charge gap e_p – e_d = 3 eV, and U = 6 eV, we estimate the gain in the exchange energy as AE ex ~ 0.05 and 0.017 eV for the bb^^ ordering ofpairs of orbitals and for the d_{z 2} – d_{z 2}– d_{x 2 – y 2}– d_{x 2 – y 2}ordering, respectively. Owing to the competition between the Coulomb and exchange interactions between the electrons on the neighboring orbitals, a certain orbital order with the structure wave vector Q = n/2 can be induced. In magnets with narrow optical bands and weak dispersion of the optical oscillation mode and the electron-phonon coupling constant ~ g k ® ^{- 1} near the band edge, the exchange mechanism possibly gives rise to change in the magnetic and orbital orders with decreasing the temperature.

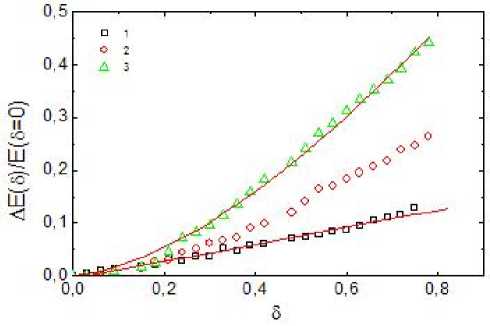
Fig. 4. The dependence of the change normalized energy state A E ( 5 )/ E ( 5 = 0) = ( E ( 5 ) - E ( 5 = 0))/ E ( 5 = 0) from the alternating exchange for the ordering of the orbitals (1) (eq. (2)) and (2) (eq. (1)), the spin Peierls 1D model (3), and power law approximation functions A E ( 5 )/ E (д = 0) = A 5 " with he parameters (3) A = 0.67 (2) and a = 1.50(4) and (1) A = 0.15(1) and a = 1 (orbital ordering).

The errors correspond to the symbol sizes

Thus, in a quasi-low-dimensional magnet with one electron (hole) on the e_g orbital and competing Coulomb and exchange interactions, the appearance of the orbital order with the structure wave vector Q = n /2 or the softening of the elastic oscillation mode near this vector is possible. The regions of existence of a plateau and of the modulated ferromagnet with the special exchange topology in the (magnetic field, exchange alternating) plane are determined.

2D Model. Let us consider a model with antiferromagnetic exchange alternation and a stripe structure for a spin S = 1 / 2. The Hamiltonian has the following form:

H = - S [ ( 1+5 )J ““ S + 1, j S + 2, j + i , j ,α

αααααα ^{+K ( S}i+ 1, j ^S i+ 1, j+ 1 ^+Si+ 2, j^Si+ 2, j+ 1 ^{) +}

αααα

^+JSi , j^Si+1 , j⁺                      (4)

+ (1 - 5) J ^aa S i a j S ^a j+ 1 +J ^aa S + 2, j S + 3, j +

+ (1 - 5) J ^aa (S + з, j S + 4, j +S i+ з, j S + з, j _{+ 1} ) ] -

- S H i s z ,

i where J(1 + 5), J(1 - 5), J(J< 0) are the exchange interactions between electrons located at the nearest d2x2 – d2x2, dx2 – y2 – – dx2 – y2, dx2 – y2– d2x2 orbitals; H is the external magnetic field, q = Jzz - J xx(yy)/Jzz is the exchange anisotropy value; K < 0 is the interchain exchange value fixed in our calculations as K/J = 1/16. The ratio of the hopping integrals are tбб /tbb = 3/4 and tap /1pp =1 /4. The exchange interactions between electrons on the dx2 _y2 and d2x2 _ z2 _y2 orbitals are Jaa IJpp = = 0.56 and JaIJpp = 0.063. This problem was solved by the described quantum Monte Carlo method. In the calculations a square lattice with L = 40; 48; 60; 72 and periodic boundary conditions in the Trotter direction and on the lattice are used. From 40 000 to 60 000 Monte Carlo steps (MCS) per site are spent to reach equilibrium and another 80 000…100 000 MCS are used for the averaging. The root mean square errors of the computed quantities lie in the range of 0 : 1 % to 0 : 6 %.

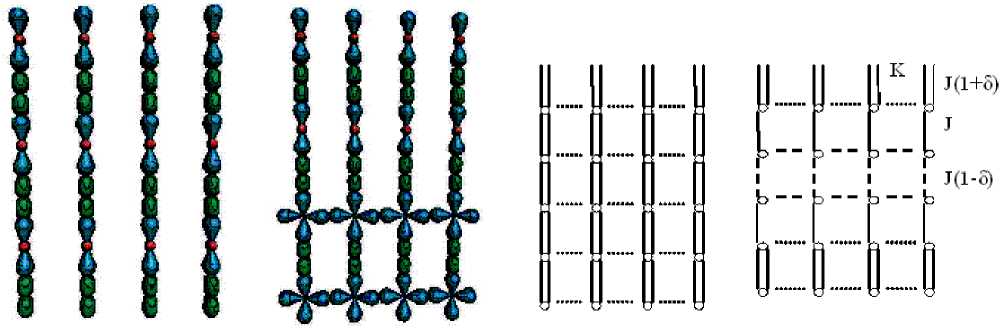
We consider two types of the orbital ordering that illustrated in fig. 5. The d _{2 x 2}– d _{2 x 2} orbitals overlap gives rise to the strong antiferromagnetic exchange and space anisotropy of the exchange interactions in a lattice, which differ in more than an order of magnitude. The magnetic properties of such a system are similar to those of a quasi-one-dimensional antiferromagnet. Alternation of pairs of the d _{2 x 2} – d _{2 x 2}, d_{x 2– y 2} – d_{x 2 – y 2} orbitals induces stripes along the [01] direction and alteration of the exchange interactions along the [10] direction, as one can see in fig. 5, c , d . The magnetic properties of systems with the two types of orbital ordering have been analyzed on the basis of a spin-spin correlation function, staggered magnetization m_s , a magnetic structure factor (eq. (3)), energy and specfic heat Ck_B / N = dE /dT .

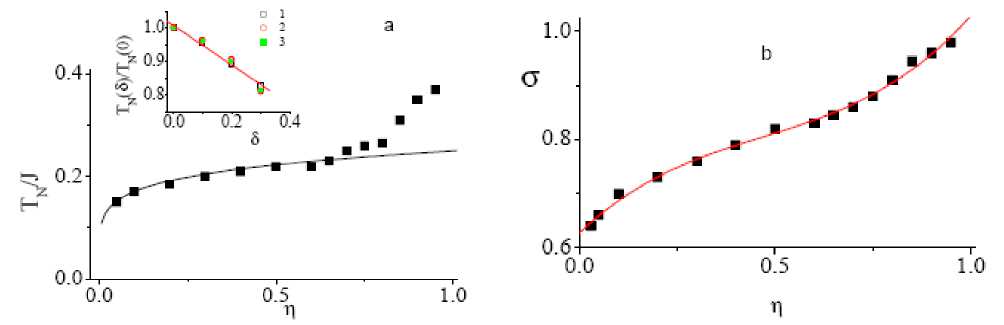
Alternation of exchange along one of the lattice directions enhances the quantum fluctuations, which results in reducing spin on site in the limit of 5...9 % in the range of parameters 0 <  5 <  0 : 4 and decreasing Neel temperature. Normalized Neel temperature is well fitted by the linear function T N ( 5 )/ T N (0) = 1 - 0 . 6 5 for a series of anisotropy parameters (insert in fig. 6). Monte Carlo simulation of thermodynamic characteristic at larger 5 and interpolation of linear function T N ( 5 )/ T N (0) indicate to stability ofAF order as compared to disordered spin state. Similar effect of reduction of spin arises from the exchange anisotropy. Staggered magnetization and Neel temperature of AF having the stripe structure rises at increasing anisotropy as shown in fig. 6. The dependence of T N ( n ) versus exchange anisotropy is better interpolated by a power function T N ( n )/ J = 1 / 4 n ^1/6 than a logarithmic law. It differ from behavior anisotropic Heisenberg antiferromagnetic with S = 1 / 2 on a square lattice that reveals the logarithmic dependence T N ( n )/ J = 2 / ln(11 / q ).

We have determined the basic magnetic properties of a two-dimensional magnet with the orbital ordering presented in fig. 5, b. As a consequence of low dimensionality of a system, the quantum spin fluctuations may cause orbital correlations and the ordering of the d2x2 – d2x2 orbitals. In this case, spin interactions are quasi-one-dimensional along a chain and favor the rise of exchange energy, which is proportional to E/J = 0.44(1 + 5). Ising-like anisotropy suppresses the quantum spin fluctuations and decreases an absolute energy value from E/J = 0.44 to 0.25 with an increase in the exchange anisotropy. With the growth of the exchange alternation along the [10] direction, energy of a 2D system decreases due to a decrease in the interchain interaction. Figure 7 illustrates energy of a 2D magnet calculated for several lattice sizes. The intersection of energies of the 1D and 2D magnets with the arrangement of bonds in a lattice as in fig. 5, c, d determines a region of stability of the 2D magnetic ordering with a stripe structure. A phase boundary separating the region of existence of a magnets with the d2x2– d2x2 and d2x2 – dx2 – y2 orbital ordering is given in fig. 8.

The quasi-one-dimensional AF ordering becomes stable at δ >  0.2; η = 0, δ > 0.34; η → 1. The ratio of exchanges in KCuF 3 is J ( d x 2 – y 2 – d x 2 – y 2 ) /J ( d 2 x 2 – d x 2 – y 2 ) ≈ 0 : 78 that corresponds to δ ~ 0.22. Exchange anisotropy is small for the cubic crystal and according to our results the ordering of the d _{2 x 2}– d _{2 x 2} orbitals is more preferably. Orthorhombic distortion of a structure in NH₄CuCl₃ induces distortion of a crystal field and the intra-atomic Coulomb interaction U_dd between electrons on the orbital. The change in distance and angle of a bond between the nearest cations modifies the overlap of integral of the wave functions of the d _{2 x 2} and d_{x 2 – y 2}orbitals. As a result, the ratio of amplitudes of the hopping integrals may vary in the wide range 0 . 1 < t _aa / t _ββ <  1, because the hopping integral is t = E ² / ( e_p – e_d + U_dd ). The exchange interaction between electrons on the d _{2 x 2} – d _{2 x 2} orbitals decreases and the ratio of exchanges J ( d_{x 2 – y 2} – d_{x 2 – y 2}) /J ( d _{2 x 2}– d _{2 x 2})

grows, that corresponds to the decreasing of an alternation parameter. As a consequence, the exchange interaction causes rearrangement of the d _{2 x 2}and d_{x 2 – y 2}orbitals and lead to strong decreasing Neel temperature in NH₄CuCl₃.

Thus, we study the exchange mechanism effect on the ordering of electrons on e_g orbitals in a square lattice by the Heisenberg model with exchange anisotropy. The ordering of pairs of the d _{2 x 2} – d _{2 x 2}, d_{x 2 – y 2}– d_{x 2– y 2} orbitals provides the two-dimensional antiferromagnetic state with a stripe structure. In the quasi-two-dimensional model with the alternating exchange the regions of the stable antiferromagnetic order in (alternating exchange-exchange anisotropy) plane are determined. The critical parameters of the alternating exchange and exchange anisotropy, at which the quasi-one-dimensional state becomes unstable are calculated.

We have analyzed the exchange mechanism of the ordering of electrons on the e_g orbitals in the quasi-low-dimensional magnets using the Heisenberg model with the special exchange topology. The gain in the exchange energy for the orthogonal ordering of orbitals pairs bb↔↔ and for the d_{z 2}– d_{z 2}– d_{x 2 – y 2} – d_{x 2 – y 2} ordering has estimated. We have found the exchange parameters associated with the relation of the exchange interaction of electrons on the

abc d

Fig. 5. d _{2 x 2} – d _{2 x 2} ( a ) and d _{x 2 – y 2} – d _{2 x 2} ( b ) orbital ordering. Arrangement of the strong intrachain J (1 + δ ) and week interchain K exchanges in a square lattice; the J – exchange is related to the overlap of d _{2 x 2 – dx 2 – y 2} orbitales; J (1 + δ ) is related to the d _{2 x 2} – d _{2 x 2} orbitals, J (1 – δ ) is the d _{x 2 – y 2} – d _{x 2 – y 2} orbitales overlap

аб

Fig. 6. Neel temperature T _N /J of the quasi-two-dimensional AF at δ = 0.3 (1) and fitting function T _N /J = η ^1/16 / 4 (solid line) as a function of exchange anisotropy ( a ). Insert: normalized Neel temperature T _N ( δ ) = T _N (0) versus alternating exchange at η = 0.25 (1); 0 . 5 (2); 0 . 75 (3). Magnetization on the site s calculated by MC at T/TN = 0 . 2; L = 60 versus exchange anisotropy ( b )

d _{2 x 2} – d _{2 x 2} and d_{x 2 – y 2} – d_{x 2 – y 2} orbitals and exchange anisotropy, at which the ordering of pairs of the d _{2 x 2} – d _{2 x 2}, d_{x 2 – y 2} – d_{x 2 – y 2} orbitals forms the two-dimensional antiferromagnetic state with a stripe structure. In a quasilow-dimensional magnet with one electron (hole) on the e_g orbital and competing Coulomb and exchange interactions, the appearance of the orbital order with the structure wave vector Q = π /2 or the softening of the elastic oscillation mode near this vector is possible. The phase diagram of the modulated quase-one-dimensional ferromagnet is determined. This diagram has a plateau m ( H ) = 1/2 on the magnetization curve in the (magnetic field, exchange alternating) plane. The region of the existence of an quasi-two-dimensional antiferromagnetic in the plane of alternation – anisotropy of exchange have been calculated. Quantum reduction of spin on site for quasi-two-dimensional antiferromagnetic with stripe structure versus exchange anisotropy has been estimated.

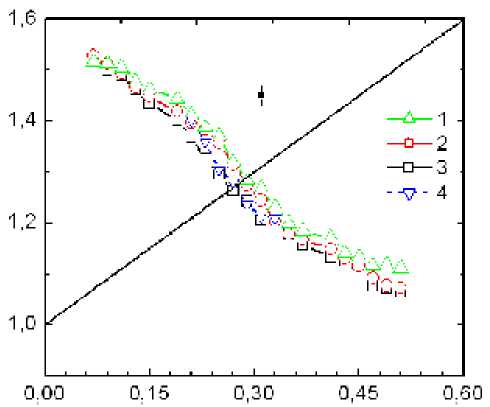
Fig. 7. Energy of a quasi-two-dimensional antiferromagnetic E _2D (see fig. 5, d ) and a quasi-one-dimensional antiferromagnetic with the strong intrachain J (1 + δ ) exchange normalized to the energy of the E _1D antiferromagnetic with the exchange ratio K / J = 1 / 16 for η = 0 . 25; L = 40(1); 48(2); 60(3);

72(4) calculated at T/T _N = 0.2 as a function of the exchange alternation. Maximum error bar denoted by square