Simulation of the mode of electron-beam welding of a thin-wall structure from AD31 alloy

Currently, a variety of technologies are used in the production of waveguide tract structures, carrying large costs due to the low reproducibility of the quality of structural joints [1–3]. The small thickness and low melting temperature of the joined products cast doubt on the feasibility of electron-beam welding in this direction [4–6]. In works [7–9] the authors simulated the electron beam welding (EBW) process for titanium alloy in order to find the optimal mode. The resulting modeling experience led the authors to the idea of investigating the possibility of applying electron-beam welding to thin-walled aluminum structures. Thus, the goal was to simulate the welding process of the investigated material with a given thickness and to compare the simulation results with the capabilities of electron-beam equipment.

The studies were based on the classical theory of thermal processes [10; 11]. The temperature distribution in a thin-layer material under the action of a moving point source on its surface can be calculated using the superposition method (source addition) [12–15]. The actual point source shown in Fig. 1 is assumed to be moving on the surface of a semi-infinite body.

The reflection of the heat flux given by the source Q1 from the boundary II is taken into account by introducing the source Q4, symmetrical to the source Q1 with respect to the boundary II, i.e. at distance 2δ from the source Q1, acting at the boundary I. In turn, the boundary I for source Q4 will be taken into account, if we introduce a fictitious source Q3, remote from the boundary I at distance 2δ. To account for the material thickness δ, a linear moving source Q2 was introduced in the simulation of the thermal process.

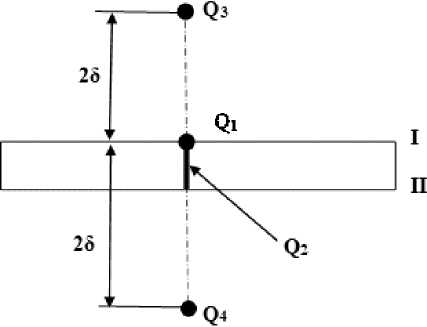
Рис. 1. Схема введения фиктивных источников для расчета температур в плоском слое

Fig. 1. Scheme of introducing fictitious sources for calculating temperatures in a flat layer

Mathematical apparatus

Adopting the selected set of heating sources and applying the superposition method [10], we obtain the final heating temperature model (1):

T^= T + T2 + T3 + T4, where T = TH +--Q==

vx t e 2ajexp

2   2.2

v т x + y

---

4 a

4 a т

dτ is the temperature of heating from an τ3/2

instantaneous point source moving on the surface;

Q ₂

‘ 2 = T H ⁺ 4nM

vx t e 2ajexp

moving linear source;

Q ₃

T 3 = T H ⁺    1----

—

v 2 τ 4 a

2^т  ( x ^{2 +} У 2 ) ^ d т .   ,

---— is the temperature from the heating of a

- - -

cρδ     4 a τ

τ

vx t e 2ajexp

-

v ²τ 4 a

-

x ² + y ² + ( z - 28 ) 2 ^ d т

4 a τ

3/2 τ

is the temperature

of

heating

from a fictitious instantaneous point source moving over the surface;

T 4 = T h +    7 ^Q 4  ₃

vx t e 2ajexp

—

v 2 τ 4 a

—

x ² + y ² + ( z + 28 ) ²   d т

4 a τ

τ3/2

is the temperature

of

heating

from a fictitious instantaneous point source moving over the surface.

When modeling the thermal process, the authors use a functional developed by them:

J =

A Ё ( T . i — T . J ' , n ^-1 ft.

T where THi = — ; Tax = max A . Tmax

The choice of parameters in the simulation was carried out according to the minimum of the functional. For example, the speed of movement of the heating source was determined by the coordinate of the position of the extreme point of the functional, as shown in Fig. 2.

Heating temperature calculations (2) were performed at integration time values corresponding to the moment of reaching the boundary of the heat-affected zone of the lower surface of the heated material, an example is shown in Fig. 3.

The maximum temperature value, which corresponds to the reference [11] properties of the studied material ( c , ρ, a , λ), is taken as the boundary of the heat-affected zone.

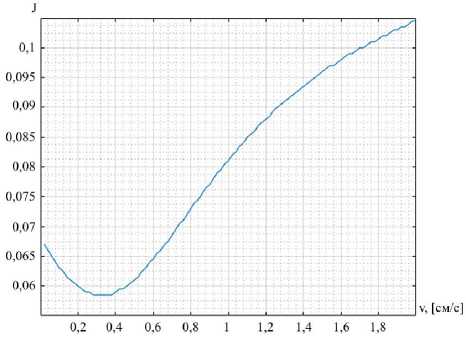
Рис. 2. График изменения функционала от скорости перемещения источника нагрева

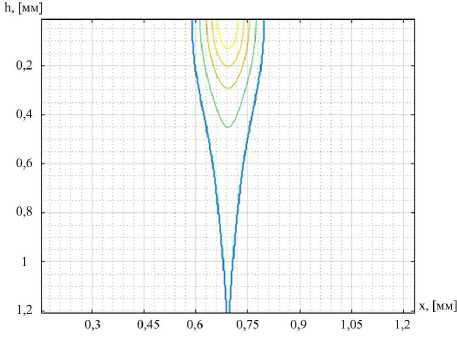
Рис. 3. Моделирование поперечного сечения зоны термического влияния:

h – толщина сварного шва; x – ширина изделия

Fig. 2. Graph of the change in the functional from the speed of movement of the heating source

Fig. 3. Modeling a Cross-Section of a Heat-Affected Zone: h – the thickness of the weld; x – product width

The criterion of optimality is the minimum of the functional under variation of the parameter for which the search for a solution is carried out. The proposed criterion is attractive because its character has a physical semantic orientation, along with this criterion has extremes at characteristic values of the varied parameters. Functional was calculated for a volume bounded by a heat-affected zone, shown in Fig. 3. Normalized numerical values of the functional were used to simulate the process.

From the physical point of view, the assumption was made that the minimum of the proposed function is proportional to the minimum temperature dispersion of heating the metal. If we take into account the volume limitations adopted by the authors of this function, then we can assume the following: in the case of uniform heating of the material, that is, the minimum temperature dispersion in the volume under consideration, the probability of uniform melting of the metal will be the highest. This will entail the formation of the weld with the best quality indicators and minimal residual stresses. The introduction of normalized indicators increases the sensitivity of the criterion, which is especially important for temperatures not exceeding the temperature of phase transitions of the materials being welded.

Results

Based on the results of studies of the behavior of the functional for different energies of the heating source, the authors formed an algorithm for calculating the parameters of the technological process, recommended in the future for the development of electron-beam welding technology.

For clarity of the information obtained in modeling, the results of calculations are summarized in the table.

Results of model calculation (2)

1	2	3	4
Q, [cal]	J	v , [cm/s]	t , [s]
3	0,0979	0,21	1,107
4	0,0958	0,27	0,869
5	0,0939	0,32	0,721
6	0,0922	0,36	0,619
7	0,0907	0,40	0,545
8	0,0892	0,44	0,489
9	0,0874	0,49	0,446
10	0,0865	0,52	0,409
11	0,0857	0,56	0,379
12	0,0837	0,60	0,355
13	0,0835	0,64	0,333
14	0,0815	0,67	0,314
15	0,0806	0,70	0,298
16	0,0809	0,74	0,284
17	0,0798	0,77	0,271
18	0,0795	0,80	0,259
19	0,0787	0,84	0,249
20	0,0782	0,86	0,239
21	0,0774	0,90	0,231
22	0,0770	0,93	0,223
23	0,0764	0,96	0,216
24	0,0762	0,99	0,209
25	0,0755	1,02	0,203
26	0,0742	1,05	0,198
27	0,0744	1,07	0,192
28	0,0743	1,11	0,187
29	0,0727	1,13	0,183
30	0,0733	1,16	0,178
31	0,0725	1,18	0,174
32	0,0727	1,22	0,170
33	0,0713	1,24	0,167
34	0,0718	1,27	0,163
35	0,0709	1,29	0,160
36	0,0705	1,32	0,157
37	0,0704	1,35	0,154
38	0,0702	1,37	0,151
39	0,0695	1,41	0,149
40	0,0693	1,42	0,146
41	0,0686	1,45	0,144
42	0,0690	1,47	0,141
43	0,0685	1,50	0,139
44	0,0680	1,52	0,137
45	0,0679	1,55	0,135
46	0,0676	1,57	0,133
47	0,0677	1,60	0,131
48	0,0676	1,62	0,129
49	0,0678	1,64	0,127
50	0,0667	1,67	0,126

The table contains the numerical values of the given complex heating source Q, according to equation (1). The numerical values of the velocity of the moving heating source v and the integration time t were chosen by analogy with Figs. 2 and 3, respectively. The calculations were performed using the simplified model (2), that is, the y and z coordinates were varied, and the x coordinate was selected by the maximum area of the heat affected zone. With such choice of modeling parameters according to the results obtained by the authors earlier [8-10], the shape of the heat-affected zone is as close as possible to the shape of the weld cross-section. Numerical values of functional J in the table were determined by equation (2) for the whole volume of material bounded by the heat-affected zone. The authors admitted the existence of correlation between the values of all columns of the table.

Based on the results presented in the table, the authors obtained a graph of the dependence of the functional J on the value of the input energy of the complex heating source, shown in Fig. 4. If we take as a basis the hypothesis about the proportionality between the quality of the weld and the numerical value of the functional (2), then according to the obtained dependence shown in Fig. 4, the authors made the following assumption that when welding thin-walled structures, there is no need for equipment that provides a highly stable very small welding current.

Thus, using a modern development tool, the authors will develop a new approach to the search for welding modes in order to obtain a stable weld quality and repeatability.

Based on the tabulated results, the authors obtained a graph of the dependence of the energy of the heating source and the speed of its movement, shown in Fig. 5. This graph is an important addition to Fig. 4. It explains how in practice it is possible to implement the hypothesis, suggested by the authors, of improving weld quality due to a proper combination of the heating source energy and its velocity.

It should be taken into account that the simulation was performed for an ideal heating source. For real welding equipment, the simulation results do not match. That is why the authors suggest determining the scale factor of a particular equipment. For this purpose it is necessary to carry out a test welding on the sample, followed by measuring of penetration depth. On the diagram in Fig. 5, it is necessary to find a point corresponding to the speed at which the welding was carried out, determine the energy Q corresponding to this point.

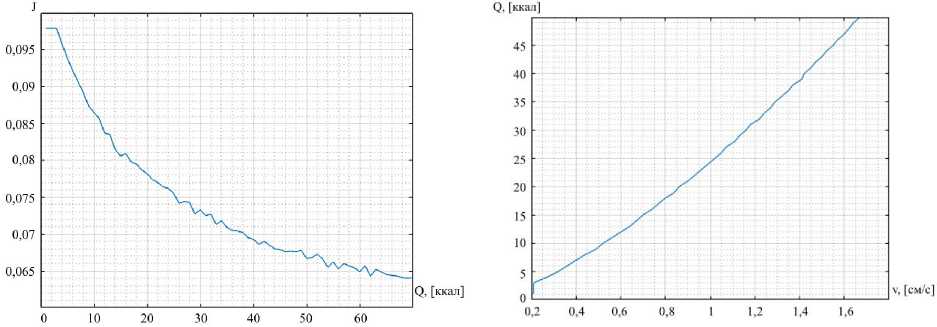
Рис. 4. График зависимости функционала от энергии источника нагрева

Fig. 4. Graph of the dependence of the functional on the energy of the heating source

Рис. 5. График зависимости энергии источника нагрева от скорости его движения

Fig. 5. Graph of the dependence of the energy of the heating source on the speed of its movement

By comparing the energy from the graph with the energy entered during welding, we obtain a scaling factor. Thus, we adapt the simulation graphs with the real heating source. The graphs obtained by the authors present the value of the functional corresponding to the real weld. Also on the basis of the received dependence diagrams it is possible to estimate a possibility to decrease the value of the functional by changing the energy of the source and the corresponding adjustment of the welding speed.

Conclusion

The article developed a new approach to the search for technological regimes in electron-beam welding. In the course of the study, the authors simulated a thin-walled plate of aluminum alloy AD31

with a thickness of 0.12 cm. As a result, by changing such values as: beam current and welding speed, the temperature distribution on the product surface during electron-beam welding was obtained, which showed that it was possible to work out a new technological process by means of simulation.

The proposed approach can be applied to electron-beam welding of elements of waveguide ducts to improve their reliability by increasing the corrosion resistance at the joints.