Simulation of vibration and noise of belt gearing

Introduction: Transmissions with flexible connection, to which strap transmissions behave to, are becoming more and more common in the technological equipment. This is especially true to the high-speed and low-rate equipment; in particular, to grinding woodworking machine tools, tool-grinding and drilling machine tools that do not have a gear drive, and their spindles are rotated through the driving belts.

^∗ The research is done within the frame of the independent R&D.

^∗∗∗ Работа выполнена в рамках инициативной НИР.

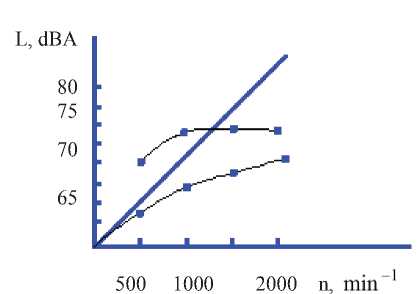
Fig. 1. The noise of belt drives at TM =22-45 N∙m·s [1]: 1- belt gear;

2 - flat; 3 - belts wedge

The main part. In the established operating mode, the engine torque is balanced by the point of cutting forces. We will designate the appropriate voltage in branches: σ - in leading branch and σ - in driven. Lengthens of branches of the tape caused by additional voltage arising at oscillations of pulleys, are defined as:

A 1 1 = Ao 1 •

l - R^-(1 - I ц 0)) = aiA^i

(E ц о EJ

( l     R.1

^A l 2 = ^A° 2 ^-| ~-- ^{( 1 —} l ⁰ ) 1 = ^a 2 ^A° 2

(E Ц 0EJ where l is the distance between the axles of pulleys, m;

Е is belt material spring constant, Pa; R1 and R2 are the radii of leading and driven pulleys, m; φ0=150° is the angle of elastic slip of flexible communication on the pulley; μ0= 0.3 is factor friction of flexible communication and pulley.

To the driven pulley, the periodic revolting moment of cutting forces ∆М = М0 sin (ωt) acts, where ω is circular rotational speed, rad/s.

Then the differential equations of the forced vibrations of pulleys look like in this case:

R ² R R

Ф1 + — азФ1--— азФ2 = 0(2)

J1

R R R

Ф ,, +--а₃ф] +--а₃ф₂ = М_о • sin to t

J2

where J 1 and J 2 are the moments of inertia of leading and driven pulleys, N∙s²∙м;

F - is cross sectional area of the tape, м²; f a ₃ = ( a 1 + a ₂ )/ a 1 a ₂

We search for the decision of this system of the equations as:

Ф1 =ф10 sin tot(3)

Ф 2 =Ф 20 ^{sin to t}

From the system, we will get:

Ф 10 =

Ц 0 R 1 R 2 F « 3

^Ф 20 =

J ₁ J ₂

to ²

—

R² F  R₂’ F )

1— + — l-a

J 1      J 2 J

Ц 0 ^{— ( to} 2

—

^R 12 ^a 3

J1

)

J 1 J ₂ to ²

to ²

—

R ₁ ² F  R ₂ ² F

J1     J2

^-a 3

Безопасность деятельности человека

The voltage change in the belt drive branches is connected with lengthening of the branches:

R 1 T 10 R 2 ^ 20

^А^ 10 =------------

^а 1

_ R 2 ^ 20 R 1 T 10

^Аст 10 =

^а 2

Then total voltage in the branches is defined as follows: ст 1 = a ₁₀ + ст ₁₀ sin to t and ст 1 = a ₁₀ + ст ₁₀ sin m t .

To determine the vibration resistances of the belt drive branches as a moving flexible connection, we use the Euler variables. Going from total derivatives to local we will receive:

d y   d y   d y d z   d y    d y

d t    d t    d t   d t    d t     d z

δ² y δ² y      δ² y      δ² y

=     ■ 2u + и ²

δ t ²    δ t ²       δ z δ t      δ t ²

where υ is linear speed of the belt movement , m / s.

Then the well-known equation of oscillations of flexible connection to the case in question takes the form:

®2 y = 2^

δ t ²       δ z δ t

- (T - u² ) Й = ⁰

m 0 δ z ²

where m0- distributed weight, kg / m; Т- tension,Н.

Belt branches tension changes in time, so the equations of oscillations respectively for the leading and driven branches take the following form:

5 ² y      5 ² y   ( F o₁₀   F Ao, .        ₂) 5 ² y

—² + 2to      = I ¹⁰ +     ¹ sin to t - и ² I—²                                  (8)

5 1 ²       5 z 5 1  ( m ₀ m ₀             ) 5 z ²

5 2 y „ 5 ² y   f F o₂₀   F Ao₂   .        ₂) 5 ² y

+ 2to       =1     -0 +      ² - sin to t - и ² I

5 1 ²       5 z 5 1 ( m ₀ m ₀               ) 5 z ²

From this system, speeds of oscillations on their own forms of oscillations are defined. On this base, considering the known dependences of the natural oscillation frequencies of the flexible coupling, an acoustic model of a linear source is accepted. The applicability of this model is confirmed by the fact that the belt length is much larger than the cross-sectional area. The sound pressure level of the source based on the data is obtained in [3, 4] and is reduced to the following form:

for к 0 h р >1

f bh b p = 0 , 03 k ^{p p}

r for к0hр>1

| P\ = 43

B f k ^{0 . 5} ( h p b p ) ^{0 . 5}

r

where κ is a wave number, 1 / m; h р and b are the belt width and thickness (respectively) m; r is the distance from the belt to calculated point, m; В is the function defining the amplitude-phase distribution of the vibration velocity on the surface of the source and is given by:

B =

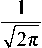
l

J exp ( - i k ₀ z cos в ) ^

z

cosβ is angle of radiation; f_kis natural oscillation frequencies of the belt, Hz, determined by the formula (5):

k  f nk )2 EJT

I                           I■

21    l ) m 0

l – length of the belt, m ; к – factor determining the natural frequency; Е –spring constant, Pa; J – section moment of inertia.

Using the representation of the elastic modulus in the complex form [19], we obtain an expression of the real part R e { f_k }

k fk 21\

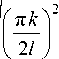
EJ T

--+ — + 22 cos n/2

m ₀   m ₀

where η - effective loss rate of oscillatory energy.

On this base, the dependences for determining the noise spectra of the belt drives are received at K0hp < 1

at к₀h _р >1

L = 20 lgB + 5 Igh p b p + 10 lgR e { f k } + 10 IgK + 127                              (14)

r where К – number of belts.

The obtained dependences allow by calculation to determine the sound pressure levels of the belt transmission taking into account the geometrical loaded parameters, and, most significantly, the loss factors of the oscillatory energy.

The acoustic system of the belt drives represents a set of three sources - two pulleys and directly flexible coupling, i.e. the belt branches themselves. These subsystems have different inflexibility and, consequently, vary in the frequency behavior. Therefore, for the identification of the sources and verification of the radiator model, the natural oscillation frequencies should be determined according to the design model (fig. 2).

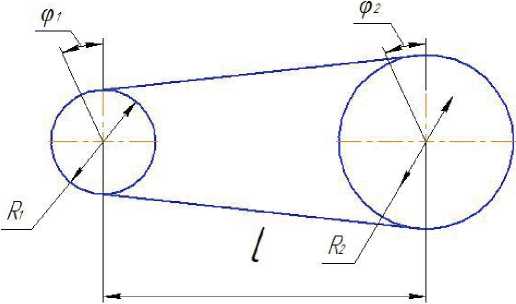
Fig. 2. Design model of belt drive

At oscillation of pulleys, the upper and lower transmission branches elongate.

By designating ∆l 1 and ∆l 2, we receive complementary elongation of the upper and lower branches

AA = R i 9 i - R 2 ^ 2 = а ₁ Аст ₁                                            (15)

A 1 2 = ^{— R} 1 ^ф 1 ^{+ R} 2 Ф 2 = a 2 ^A^ 2

In case of oscillations, both the inertia moment and the tension moment in the belt drive branches affect each of the pulleys. Then, the differential equations of the natural oscillations of pulleys look like:

• ••    R 2 Fa.

Ф 1 ⁺ —— Ф 1

J ₁

—

RRFa

¹ 2   ³ Ф 2 = ⁰

J ₁

• ••    R,R.Fa.

Ф 2 ^{+   1} 2   ³

J ₂

Ф 1

—

R ² Fa

³ Ф 2 = ⁰

J ₂

.      _    a i ^{+ a} 2

where a ₃ =------- .

a ₁ a ₂

From the system of the equations (16), the natural oscillation frequencies are defined:

f i = 0 ;f = —. RFa ₃1 R ¹ + R 2 ¹            2n\ ^{1   3} ( J 1    J ₂

Безопасность деятельности человека

Conclusions:

The research results have shown that the sound radiation of the pulleys has a narrow-band spectrum, and natural frequencies lie in a low-frequency range. The belt drive as a system with the distributed mass has a broadband spectrum of natural oscillation frequencies.

According to the obtained dependences, the growth of the factors of the oscillatory energy loss results in a significant reduction in the vibroacoustic characteristics of both the belt transmissions and the whole spindle unit.