Sine Cosine Taylor Like Technique for Connected Component Detector by ICNN Simulation

Published Online April 2012 in MECS DOI: 10.5815/ijigsp.2012.03.05

Cellular neural network model is still used to solve some real time application problems and it is not exhaustive. This is indeed due to its nature of extending accuracy in order to determine approximate solutions. It is noticed that cellular neural network (CNN) is the core of the revolutionary analogic cellular computers, a programmable system based on CNN-UM. Analogic CNN computers mimic the anatomy and physiology of many sensory and processing biological organs. It is understood that the characteristics of cellular neural networks (CNNs) are analog, time-continuous, nonlinear dynamical systems and formally belong to the class of recurrent neural networks.

The introduction of CNN paradigm proposed by Chua and Yang [1, 2] has become fruitful soil for all researchers in diversified fields to execute their sophisticated tasks with linear and non-linear type problems. Notably, this artificial neural network offers a remarkable ability of integrating complex computing processes into compact, real-time programmable analogic VLSI circuits and many important applications in signal and real-time image processing.

Roska et al. [3] have presented the first widely used simulation system which allows simulation of a large class of CNN and is especially suited for image processing applications including signal processing, pattern recognition and for solving ordinary and partial differential equations [6-11].

The model of CNNs [1, 2] is a very appropriate framework for systematic design of smart-pixel chips. CNNs consist of regular arrangements of cells-topologically identical to a sensor array, but their cells are only locally connected, and thus, require simple routing. In addition, the enormous body of literature on CNN theory and applications demonstrates outstanding features of this paradigm for array-processing [12]. It is known that CNN chips transform an input image [ i_c ] into an output matrix array [ y c ] via a dynamic process of interactions among the computing cells associated to pixels. The distinctive feature of CNN paradigm is that these interactions are local, limited for each cell to a reduced set of neighbors located within a distance r in the grid. Specifically, there is a wide catalog of image processing tasks available for networks where parameter r (called the neighborhood radius) is unity – which is very appealing for VLSI implementations because connection among units is made by abutment, thus requiring no extra routing.

Espejo et al. [12] present a continuous-time CNN chip [1, 2] for the application of connected component detection. The global dynamic behavior of a three-cell connected component detector CNN is described by Civalleri and Gilli [13]. Also, Cruz and Chua [14] present the first working chips to implement a CNN. They have integrated in a CMOS 2-pm technology intended for connected component detection processing applications. The operation is made in a continuous time using analog circuitry. The design, fabrication and testing of these chips are presented. Implementation of connected component detector in CNN paradigm is discussed and illustrated with example by Matsumoto et al. [15, 16]. Chen et al. [17] discuss in detail about image-processing algorithms realized by discrete-time cellular neural networks and their circuit implementations.

Feng et al. [18] propose a new automatic nucleated cell method with improved cellular neural networks and prove its efficiency. They also prove that the running speed is comparatively high due to the easy hardware implementation and high speed of CNN. Harrer et al. [7] discuss about three popular single step algorithms for solving system of nonlinear differential equations of cellular neural networks. Typical behavior of these algorithms is also described, where simulation examples are given, and their relative advantages and disadvantages discussed. Using the existing RK-Butcher fifth order method, the problem of connected component detector CNN simulation has been addressed by Murugesh and Murugesan [19]. A detailed illustration related to LTE, GTE and error estimates and control for fourth order and four stage RK numerical algorithms are eventually reported by Senthilkumar [20] in addition to real time application problem. A new fourth order embedded RKAHeM(4, 4) method and algorithm based on Runge-Kutta arithmetic Heronian mean with error control is proposed by Ponalagusamy and Senthilkumar [21, 22] to solve real time application problems in image processing under CNN environment efficiently.

Ahmad and Yaacob [23-25] introduce sin-cos-Taylor-like technique to solve stiff ordinary differential equations and prove that the results obtained are better than other techniques. They also pointed out that the technique requires extra work to evaluate a number of differentiations of the function involved. Their result shows smaller errors compared to results from the explicit classical fourth-order Runge-Kutta (RK4) which is of order 6 [23]. Runge-Kutta (RK) techniques have became very popular and efficient for computational purpose [26-29] and many real-time problems. Burrage and Petzold [30] illustrate order reduction for RK methods applied to differential-algebraic systems and stiff systems of ODEs. In particular, the RK algorithms are used to solve differential equations efficiently, i.e. equivalent to approximate exact solutions by matching ‘n’ terms of the Taylor series expansion. The RK-Butcher algorithm has been introduced by Bader [31, 32] to find truncation error estimates and intrinsic accuracies and early detection of stiffness in coupled differential equations that arises in theoretical chemistry. Oliveria [33] introduces the new popular RK-Gill algorithm to evaluate effectiveness factor of immobilized enzymes.

In this paper, the connected component detector under ICNN model with sine cosine Taylor like technique is executed and compared to the explicit Euler, RK-Gill, RK-classical fourth order. It is pertinent to note that a different treatment has been carried out using explicit sine cosine Taylor like technique to solve connected component detector via ICNN simulation which is a combination of polynomial and an exponential function. The rest of the paper is organized as follows: a brief outline on improved CNN model is given in section 2. Section 3 deals with different numerical integration techniques. Section 4 discusses the bifurcation behavior of connected component detector for ICNN simulation with its corresponding simulation results with a conclusion presented in section 5.

• II.    STRUCTURE AND FUNCTIONS OF

IMPROVED CELLULAR NEURAL NETWORK

A processing is governed by a set of nonlinear differential equations, one per cell. The architecture of standard M × N CNN [1, 2] is composed of cells C ( i , j ) where 1 ≤ i ≤ M ; 1 ≤ j ≤ N . M × N can be understood to be the dimension of a digital image P to be processed. The dynamics of each cell is given via the following equation:

dxij (t) -1

c-г-=-^x j ⁺ L a k , 1 У . + k ⁺ dt R          k , l e Si. , j ( r )

L  bk,iui+j+zij k, l e Sij( r)

- 1

= x R ij

rr

+ L L ak, ly+k  +

k=-rl=-r rr

L L b k , i u i + k j+i ⁺ zi,i k =- rl =- r

where x_i, , y_i, , u_i, and z_i, represent the state, output, input, and threshold variables, respectively. S_i, ( r ) is the sphere of influence with radius r . a k,l and b k,l are elements of the A template (feedback template) and B template (feedforward template), respectively. The output y i, is piecewise linear function. c and R determine recall time. The constraint / conditions are given by

| x i j (0) | <  1, | u i j | <  1 where c > 0 and R > 0.

By taking c and R to be at 1, lead to the output function to be defined as

' 1

i , j

*

y ^ = f ⁽ xij ) = 1 xij

I x «l< T *

- 1

x

- T *

MN

T" =LL P (i, j)/(MN) i =1 j=1

where P ( i , j ) denotes the unitary grayscale of the pixel ( i , j ) in the input image P . M × N is understood to be the dimension of the digital image P . It is obvious that the range of T * is (0,1).

variable x ij is stored in the constant k ₁ ^ij . This result is used in the next iteration to evaluate k ₂ ^ij . The same process is repeated to obtain k ₃ ^ij and k ₄ ^ij .

• III.    NUMERICAL INTEGRATION TECHNIQUES

The ICNN is described by a system of nonlinear differential equations. It is necessary to discretize the differential equation to perform behavioral simulation. For computational purpose, a normalized time differential equation describing CNN is used by Nossek et al. [8].

dx ij ( п т )

f (x(пт)) =   dt—=- xy (пт)+ rr      rr

E E ak, i^+k ,y+i+E E bk, iui+k ,y+i+zu k=-rl=-r               k=-rl=-r

У у ^{( n т )} = 2 [ ^X y ⁽ n ^т ) + ¹1 ^-1 x y ^{( n т ) - 1 ]} ,     ⁽⁵⁾

where т is the normalized time. To solve initial value problem, well established single step techniques of numerical integration techniques are used [7]. These techniques can be derived using the definition of the definite integral,

^T n + 1

X y (( n + 1) т ) - X y ( п т )) = J f ' ( x ( п т )) d ( п т ) (6)

т

Explicit Euler, improved Euler predictor-corrector and fourth order (quartic) Runge-Kutta are the most widely used single step algorithm in CNN behavioral raster simulation. These techniques vary in the way they evaluate the integral presented in [7].

• A.    E XPLICIT E ULER M ETHOD

Euler’s technique is the simplest of all algorithms to solve ordinary differential equations. It is an explicit formula which uses Taylor series expansion to calculate an approximation,

X y (( n + 1) т ) = X y ( n т ) + т ' ( X ( n т ))            (7)

• B.  RK-G ILL TECHNIQUE

The RK-Gill technique discussed by Oliveria [33] is an explicit technique which requires the computations of four derivatives per time step. The increase of the state k f = f'(Xy ( пт))                               (8)

k ’ = f ' ( X y ( п т ) + 2 k ’ )

i                                  1 1i 1 i k3 f (Xy(пт)+ \J2 2)k 1 )+ (1 ^2)k2)

k 4 = f ' ( X y ( п т ) - -12 k 2 + (1 + -2-) k ? ).

Hence, the final iteration is a weighted sum of the four calculated derivates per time step given by

X_y (( n + 1) т ) = X_y ( п т ) +

^[ k f + (2 - 72) k i + (2 + V2) k i + k f ].

• C.    RK-C LASSICAL F OURTH O RDER M ETHOD

The RK-classical fourth order method is an explicit method which requires the computation of four derivatives per time step. The increase of the state variable x i is stored in the constant k ₁ ⁱ . This result is used in the next iteration to evaluate k ₂ ⁱ and the process is repeated to obtain k ₃ ⁱ and k ₄ ⁱ .

^k i^y =^т ‘ ( ^X y ^{( п т} ))

k y = Tf ' ( X y ( п т ) + 2 k f )

k 3i = У ' ( X ,y ( п т )) + 2 k 2

^k 4 = ^т' ' ( ^X y ^{( П т} )) ^{+ k} 3 ^y                          (¹⁰)

Thus, the final iteration is a weighted sum of the four calculated derivatives per time step which is given by

X_y (( n + 1) т ) = X_y ( п т ) +

[( k f + 2 k f + 2 k f + k 4)/6]

where f (.) is computed as in equation (2).

• D.    S INE C OSINE T AYLOR L IKE T ECHNIQUE

Ahmad and Yaacob [23-25] discuss explicit one step technique using the composition of a polynomial and an exponential function.

1У. .1 = X + h (L + h (f +

h (f^ + h (f- + hf-)))) +624120

f„5(sin(z„h) + cos z„h))

z_n ⁶                                      (12)

(exp z.h) —1 — hz„ (1 + hz„ (2 +hz„ (^ + hz„ (— + znh-)))))n6 n24 120

IV. Experiment simulation and result analysis

• A.    S IMULATION B EHAVIOR OF C ONNECTED Component Detector Via ICNN

It is important to point out that the statement of the problem is to yield accurate hand written characters and images; a statement of the approach towards solving the problem is under improved CNN architecture and the most important simulation results are demonstrated through graphical outputs. CCD is one of the application in data compression, image processing, pattern recognition, and in many other important features of traction process discussed by Matsumoto et al. [15, 16]. The CCD is selected for simulation due to state variables which frequently change their sign during transient time and it is referred as a “worst case network” from observer’s point of ringing of variables. Figure 1(a) shows a character recognition system of CCD with initial pattern behavior and cloning templates given in Figure 1(b).

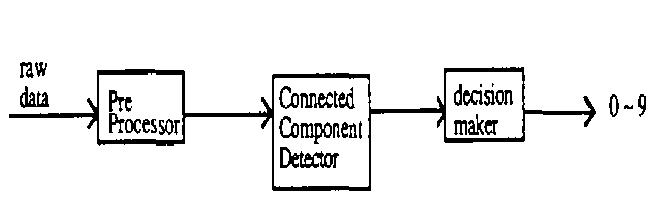
Figure 1(a). A character recognition system

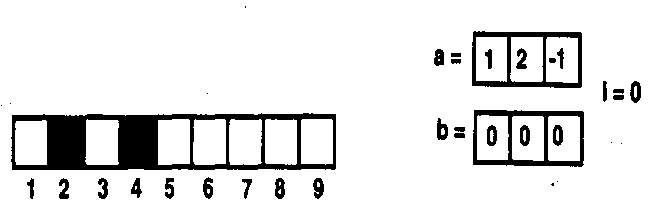
Figure 1(b). Initial pattern and cloning templates

Figure 2 demonstrates transient state variables of cell 6 obtained by various numerical integration techniques. The reference function is constructed by employing sine cosine Taylor like technique with a much smaller step size (Δ t ref = 0.0001). The larger error term of an Euler technique occurs due to “run after characteristic”. The zero crossings are shifted to the right and extreme values are larger than the ones in the original system. RK-Gill algorithm reduces extreme values and sine cosine Taylor like technique approximates the state variable best due to its computational effort. If a step size (Δ t ) value exceeds 1.521 then the modified Euler technique becomes unstable and the state variable starts to oscillate. To speed up simulations, it is essential to know the maximum step size of all the algorithms.

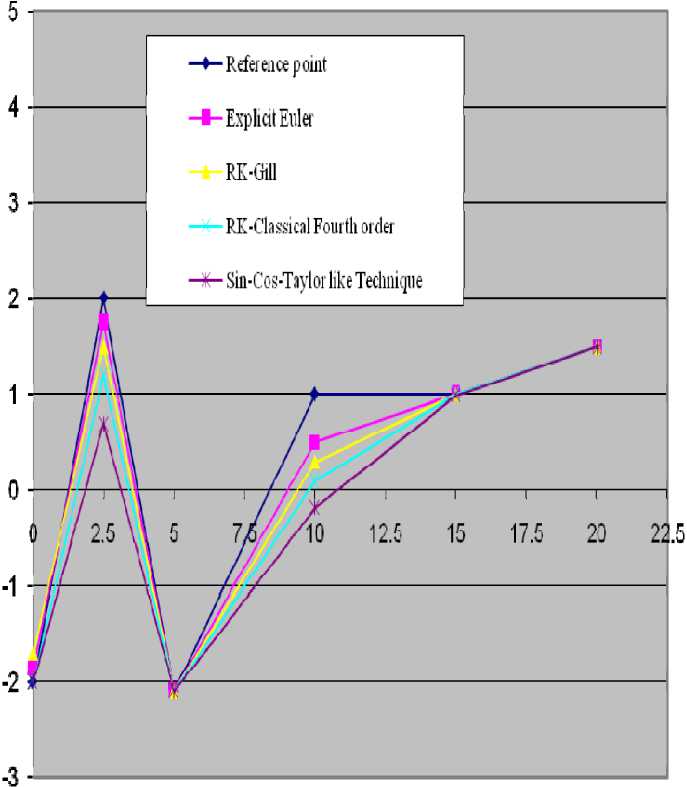
Figure 2. Simulation results for Δ t = 1 from t = 0 to t = 20.0

For very large step size, the system starts to converge but the transient behavior of the state variable is approximated roughly. If the computing time is compared significantly then the performance of an algorithm depends on the computational effort for a single time step as well as on the maximum step size, which still leads to convergence. It is easy to compare the necessary time for a single iteration step divided by the maximum step size.

Euler / modified Euler algorithm fallout in the shortest simulation time and it is useful for simulations where high accuracy of the transient of the state variables is not obtained. This is specifically valid for templates where correct dynamics behavior depends primarily on the sign of derivatives and their values.

Finally, accuracy of the algorithm as a function of the step size is shown in Figure 3, where error term ε is defined as maximum deviation of state variable x_i j from its reference function x ˆ ^ij ,

^J = max |х^( tk ) - xij( tt )|.

Figure 4 illustrates the modified Euler algorithm which is unsuitable for low value of ε . The error function increases severely even for a relative small step size. Sine cosine Taylor like technique yields accuracy over a large range of step size, but the error term grows when a “threshold” is exceeded. Non-monotonic behavior of ε is caused by shifting the timing instances at which the state variables are evaluated. So, worst case time instances occur and achieve a locally smaller ε when the step size is increased.

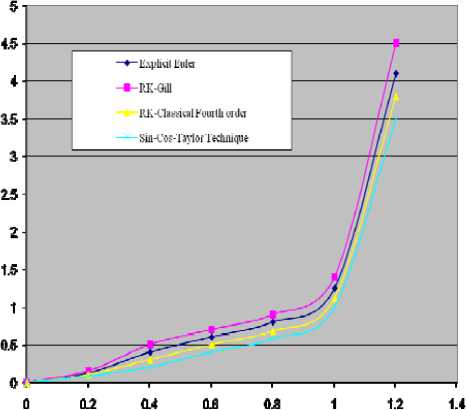
Figure 3. Computation accuracy ( ε ) versus step size (Δ t )

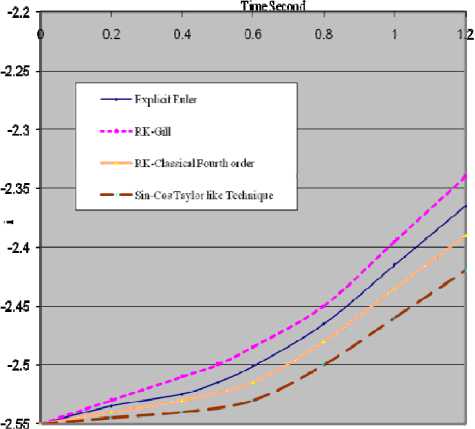
Figure 4. Bifurcation point vs step size

• B.    B IFURCATION B EHAVIOR OF C ONNECTED Component Detector by ICNN

  A selected dependent parameter and the simulated system near a bifurcation value is discussed in [10]. Let us consider the template and initial pattern, where the output of cell 3 is white for current i = -3 and black for current i = -2. In between bifurcation value is determined by interval nesting in a number of simulations. The outputs in Figure 4 show bifurcation point versus step size. The accuracy of i is within 0.0001 caused by large error term of modified Euler technique resulting in an erroneous bifurcation value. If the step size is large, the proposed sine cosine Taylor like technique yields better result. Figure 5 shows cloning template, initial pattern and output patterns.

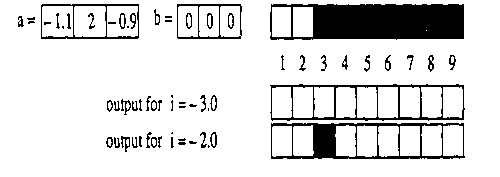
Figure 5. Cloning template, initial pattern and output patterns

• V. Conclusion

This paper sheds some light on different numerical integration algorithms on connected component detector simulation under improved cellular neural network paradigm to enhance accuracy of hand-written character and image recognition system.

It is noticed from simulation that there is a trade-off between speed and accuracy of numerical integration techniques. Thus, it is useful to implement different algorithms under improved cellular neural network CCD simulator. Sometimes, lower order algorithms are preferred for very fast tool when correct final state is of importance. But in contrast, the unusual good convergence feature of this algorithm can be explained by the fact that the desired behavior of ICNN depends primarily on qualitative dynamics of state variables. If the end user is interested in transient of state variables, the sine cosine Taylor like technique is more suitable, since the chosen step size of 0.5 gives a good transient behaviour.

Acknowledgment

The first author would like to extend his sincere gratitude to Universiti Sains Malaysia for supporting this work under its post-doctoral fellowship scheme. Much of this work was carried out during his stay at Universiti Sains Malaysia between April 2011 and

March 2012. He wishes to acknowledge Universiti Sains Malaysia’s financial support.