Синергия геометрических инвариантов двумерных многообразий на основе математического и компьютерного моделирования

Математическое образование в России и во всем мире претерпевает в последние десятилетия существенные изменения, если не сказать кризисные явления как объективного, так и субъективного характера. Цифровизация школы и вуза объявлена главным трендом российского образования и призвана дать ответы на «взрывное» появление новых компетенций, изменение рынка труда и открытости глобального информационного пространства. В то же время, интеллектуальные операции мышления (понимание, конкретизация, абстрагирование, обобщение, моделирование, аналогия, ассоциации и т.п.), лежащие в основе формирования универсальных учебных действий обучаемых, по разным объективным и субъективным причинам перестали углубления опыта личности на основе текущего его состояния, формирования и развития мотивационной сферы учения, интеллектуальных операций и способностей с опорой на фундирующие механизмы и наглядное моделирование возможностей проявления и коррекции функциональных, операциональных и инструментальных компетенций в освоении сложных конструктов и процедур математики. Именно управление образовательными процессами на базе освоения сложного знания средствами математического и компьютерного моделирования способны дать мощный мотивационный заряд к изучению математических дисциплин; как следствие, повысится интерес к освоению математики с реальным развитием теоретического и эмпирического мышления (сравнение, аналогия, анализ, синтез и т.п.). При этом возможность адаптации современных достижений в науке к школьной математике и компьютерного интерактивного взаимодействия с учебным предметом усиливает развивающий эффект и повышает учебную и профессиональную мотивацию, выявляет связи с реальной жизнью и практикой, создает феномен проявления синергетических эффектов в освоении сложного математического знания. Студент уже сейчас должен знакомиться с нелинейным стилем мышления в постнеклассических науках, знать и находить ассоциации в реальной жизни таких феноменов коллективной упорядоченности как эффект Жаботинского-Белоусова, ячейки Бинара («дорога гигантов» в Ирландии), теория Гинзбурга-Ландау сверхпроводимости в системе квантов, уравнения Лотки -Вольтерра в системе «хищник-жертва», снежинка Коха и цилиндр Шварца, сценарий Ферхюльста и «эффект бабочки» странного аттрактора Лоренца и т.п. Ведущая идея такова: ключевым аспектом феномена проявления синергетических эффектов в обучении математике сложного знания на основе адаптации современных достижений в науке является возможность актуализации этапов и исследования характеристик освоения сущности сложных математических знаний, явлений и процедур, создания условий для коммуникаций и диалога культур, выявления атрибутов самоорганизации содержания, процессов и взаимодействий (аттракторы, точки бифуркации, бассейны притяжения, итерационные процедуры и т.п.) в ходе освоении «проблемных зон» математики. Тем самым, настоящее исследование представляет собой попытку разработки технологии адаптации современных достижений в науке к обучению вузовской математике на основе компьютерного моделирования и дизайна, наглядного и математического моделирования сложного знания в «проблемных зонах» математического образования с проявлением синергетических эффектов и выявления новых побочных продуктов исследования на основе самоорганизации когнитивной деятельности.

Методология, методы, технологии

Реализация объявленной технологии связана с освоением обучающимися сложного знания средствами математического и компьютерного моделирования в насыщенной информационно-образовательной среде. Эффективным инструментом освоения сложного математического знания и развития интеллектуальных операций мышления обучающихся может являться исследование и адаптация к школьной или вузовской математике современных достижений в науке, ярко и значимо представленных в приложениях к реальной жизни, развитию других наук, высоким технологиям и производствам.

Выделим следующие системно-генетические контексты проявления синергии в математическом образовании в вузе (ср. А.А. Вербицкий [1]).

• 1.    Процессуальные контексты. Базовым понятием представленной концепции адаптации современных достижений в науке является принцип и

• технология фундирования опыта личности (Э. Гуссерль [1], В.Д. Шадриков, Е.И. Смирнов [9-10] и др.). Поэтому концепция фундирования процесса становления личности выступает как эффективный механизм преодоления профессиональных кризисов становления специалиста и актуализации интегративных связей между наукой, профессиональным образованием и школой. Адаптационные процессы рассматриваются учеными психологами и педагогами как динамический комплекс интегрального взаимодействия внутренних результатов (системы знаний, умений, установок, компетенций, ценностей) и адекватных механизмов приспособления личности к изменениям внешней среды и результатам деятельности с развивающим эффектом (А.А. Реан [8], Ю.И. Толстых [9], С.И. Сороко [11] и др.). В соответствии с С.Н. Дворяткиной и С.А. Розановой [12] таковыми могут быть синергетические эффекты реализации адаптационных процессов: когнитивный, мотивационный, профессиональный, креативный, социально- экономический и духовно-нравственный. Процессы создания мотивационного поля для исследования сложных математических конструктов требуют компьютерного дизайна и наглядного моделирования современных достижений в науке (странный аттрактор Лоренца, нечеткие множества и fuzzy-logic, губка Менгера, сценарий Ферхюльста и т.п.). Выстраивание иерархий в развертывании сущности обобщенного конструкта «проблемной зоны» на основе параметризации и абстрагирования, поиска точек бифуркации и бассейнов притяжения средствами построения итерационных процессов на основе информационно-технологической поддержки создают механизмы адаптации сложного знания к школьной и вузовской математике.

• 2.    Содержательный контекст проявления синергии в математической деятельности как раз и является тем сензитивным механизмом, который позволит актуализировать факторы успешности решения творческих задач на основе исследовательской активности и самоорганизации обучающихся. Поэтому основным средством проявления синергии математического образования и механизмом формирования исследовательского поведения школьников в процессе обучения математике мы считаем разработку и внедрение в учебный процесс исследовательских практико-ориентированных сложных задач в «проблемных зонах» в форме комплекса многоэтапных математико-информационных заданий (М. Клякля, В.С. Секованов, Е.И. Смирнов [13-14] и др.). Исследовательская деятельность обучающихся реализуется в специально организованной среде (например, ресурсных занятий [15]) на фоне роста мотивов самоактуализации и самоорганизации, выявления приоритета ценностных ориентаций в математической деятельности. Немаловажным фактором содержательного контекста проявления синергии математического образования является продуктивная деятельность по исследованию новых математических свойств и характеристик обобщенных конструктов самоорганизации : фрактальных объектов, математических моделей неустойчивости решений нелинейных динамических систем, средств кодирования и шифрования, клеточных автоматов, нечетких множеств и fuzzy logic, компьютерного моделирования многогранных поверхностей цилиндра Шварца, стохастических структур на странных аттракторах и т.п. (В.С. Секованов, Е.И. Смирнов, С.Н. Дворяткина [16], Е.И. Смирнов, А.Д. Уваров [17]).

• 3.    Личностно-адаптационный и социальный контекст проявления синергии математического образования. Взаимодействие человека с миром и людьми активизирует его внутренние потенциалы, что выступает основой его самопознания, саморегуляции и самоактуализации, обеспечивая тем самым его личностное саморазвитие. В связи с этим, особое внимание нами уделено рассмотрению проблем организации группового взаимодействия обучающихся, являющегося важнейшим источником их самоактуализации и развития, стимулом для творческой активности и дальнейшего личностного роста. Фундирующие процедуры перехода от наличного состояния сущности к обобщенному потенциальному ее

развитию в форме идеального объекта (процесса или явления, состояния личностных качеств) являются многоэтапными, полифункциональными, направленными и интегративными по актуализации внутри и межпредметных связей. Личностноадаптационный компонент связан с выраженностью характеристик и качеств личностного развития и адаптации обучающегося в процессе освоения современного научного знания в направлении самоактуализации («мне это интересно»), самоопределения («что я могу сделать»), самоорганизации («я способен управлять процессом»), саморазвития («я могу сделать что-то новое») [18].

Синергетический    эффект    исследования многогранных

поверхностей цилиндра и конуса Шварца

Пример 1 . Множественное целеполагание процессов актуализации понятия площади поверхности приемами исследования «площади» цилиндра Шварца (содержательный аспект) . Возникают иерархии вопросов, связанных с исследованием многогранных поверхностей цилиндра Шварца и решаемых средствами компьютерного и математического моделирования исследовательской деятельности в малых группах школьников в дистанционной среде или в форме исследования многоэтапных математико-информационных заданий [13]. На рисунке 1 представлен фрагмент фрактальной поверхности «кубка Шварца» [15].

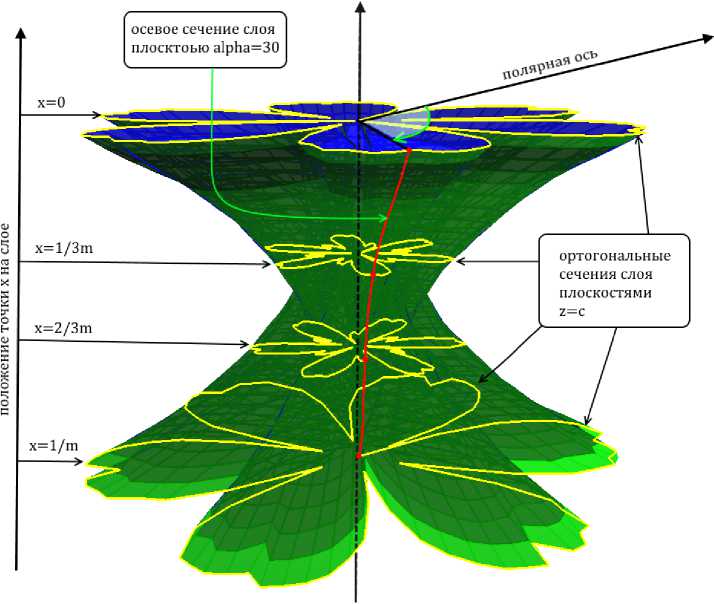
Рис.1. Кубок Шварца

Пример 2. Рассмотрим конус высоты H и радиуса R . В результате проделанных манипуляций, получим некоторую поверхность – конус Шварца (рис. 2).

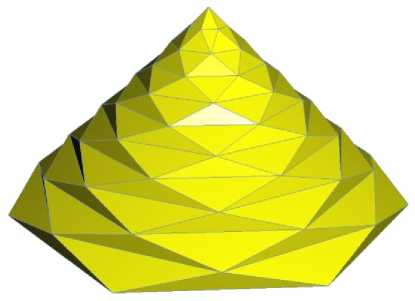
Рис.2. Конус Шварца

Выведем формулу для площади боковой многогранной поверхности конуса Шварца. Следующее изображение демонстрирует поведение площади поверхности конуса Шварца с высотой H = 1 и радиусом R = 1 при m = n , при этом 200 <  n <  800 .

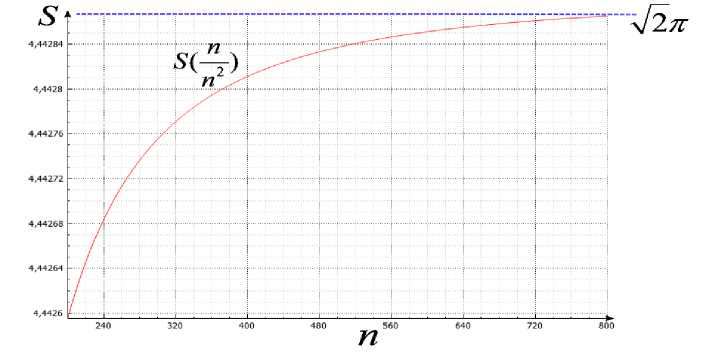
Рис.3. Зависимость площади конуса Шварца от m lim n,m^ю n

Результаты

Таким образом, выявлены и характеризованы содержание, компьютерный дизайн и технология исследования обобщенных конструктов выявления сущности одной из «проблемных зон» вузовской математики – площади поверхности в детализации нелинейной динамики роста площадей многогранных комплексов при измельчении триангуляций боковой поверхности цилиндра или «сапога» Шварца средствами компьютерного и математического моделирования. Выявлены и характеризованы точки бифуркации, бассейны притяжения, вычислительные процедуры и флуктуации параметров состояния, компьютерный дизайн и побочные результаты исследования «площади» боковой поверхности регулярного и нерегулярного цилиндра Шварца. Выстроены иерархии форм и средств исследовательской деятельности школьников: ресурсные и лабораторно-расчетные занятия, комплексы многоэтапных математико-информационных заданий, проектные методы и сетевое взаимодействие.