Сингулярные модели передаточных и импульсных переходных функций распределенных объектов

Для линейных объектов с сосредоточенными параметрами базовыми моделями являются передаточная функция W ( p ), характеризующая линейную связь между трансформантами входа и выхода, и весовая (импульсная переходная) функция g ( т ) , являющаяся реакцией объекта на идеальное импульсное воздействие, связанные преобразованием Лапласа. Для типовых сосредоточенных объектов W ( p ) и g ( т ) имеют простую форму и обеспечивают получение конструктивных решений для временных траекторий переходных процессов.

Для распределенных объектов импульсными переходными функциями являются функции Грина краевых задач для соответствующих дифференциальных уравнений в частных производных [1] и передаточными функциями их трансформанты Лапласа. Эти конструкции достаточно сложные, приводят к неудовлетворительно сходящимся рядам и малопригодны на практике. Далее будем рассматривать распределенные объекты, описываемые параболическими управлениями теплопроводности.

Импульсные переходные функции G(т, x) для них находятся как обобщенные решения уравнения д G дт

д 2 G     . л

--2 = ®(т,x), дx

где го ( т , x ) сингулярные функции дельтаобраз-ного типа, определяемые видом соответствующих краевых задач, т и x соответственно, временная и пространственная координаты с областью определения т е [0, да ) , x е [0, 1] •

Для одномерного протяженного объекта единичной длины с краевыми условиями первого рода, и симметрии ® 1 ( т , x ) = 5 ( т ) 5' ( x - 1) и точное решение для передаточной функции имеет вид [1]

W ₍ ) = exp(7 px ) + exp(-7 px ) = ch ⁽ ^х )

^{1 Р}’      exp(7 p ) + exp( - ^p )     ch (T p ) ’ ⁽²⁾

где p – оператор преобразования Лапласа.

Конструктивного представления для импульсной переходной функции, отвечающей обращению по Лапласу (2), в рамках стандартных, аналитических функций не существует, и для этих целей (2) представляется бесконечным рядом экспонент да

Wi/’,^x) = X ¹) k ^(exp42 k +^{1 -} x )/ p ) I ^ex|⁽<2 / x ^{+ 1 + x)}^p )). (3) k =0

Все члены ряда (3) имеют одинаковую стандартную форму и единообразным способом элементарно трансформируются во временную область описания. Однако практическое использование (3), и соответствующего ему оригинала, встречает серьезные затруднения, связанные со сходимостью рядов.

Для больших значений p и, соответственно, для малых моментов времени т члены ряда (3) быстро убывают, и для удовлетворительного описания достаточно использовать первые несколько членов (часто на практике два – три). Так, двухчленное представление, соответствующее (3), имеет вид

W 1 ( p , x ) « exp( -T p (1 - x )) + exp( -7 p (1 + x )). (4)

Отвечающее ему временное представление для импульсной переходной функции имеет форму

G 1( t , x ) »

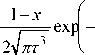
(1 - x )² ) 4 т  J

+

1 + x

I 3 2V пт

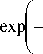
(1 + x )² 4 т

Представления (4), (5) эффективны для малых т и больших p , однако при малых p и больших временах т >>  1 использовать ряд (3) , а также приближение (4) реально невозможно из-за неудовлетворительной сходимости (3). Для получения конструктивных решений в этом случае можно непосредственно разложить (2) в ряд Тейлора.

Первые два члена соответствующего разложения W(p , x ) при p ^ 0 имеют вид

ла членов рядов приближений и разных граничных условий.

На основе сопряжений первых двух членов разложений (4), (6) и (8) конструируется следующее простейшее приближенное представление для передаточной функции

W ( p , x ) « exp( -7 p (1 - x )) + exp( -V p (1 + x )) -

- ¹ + p ⁽x ---1) exp( - 2^).       (9)

W i ( p , x ) ~ ¹ + ^С x ^- 1) p + ••••       (6)

Представление (6) удовлетворительно описывает решение (1) при малых p (больших т ), однако оно имеет принципиально иную форму чем ряд экспонент (3), и обратными трансформантами Лапласа от (5) являются сингулярные обобщенные функции времени

Приближение (9) имеет форму, отражающую структуру параболического оператора, и асимптотики (8) на границах p ^ 0, p ^ да совпадают с ( 4), (6).

Приближенным описанием импульсной переходной функции, отвечающей оригиналу от (9) является квазиасимптотическое представление

1 2

^( т , x ) = 5 ( т ) + ^( x ² - 1) 5' ( т ) + ..., (7) применять которые в рамках обычных классических функций затруднительно.

Полученные приближенные описания передаточной функции (4), (6) и импульсной временной функции (функции Грина) (5), (7) являются сингулярными асимптотическими представлениями на разных границах т = 0 и т = да временного интервала, описывающими существенно различные черты поведения распределенных объектов: (4), (5) – динамику импульсных, резконестационарных режимов, определяемую, главным образом, структурой оператора в частных производных, и (6), (7) – стадию квази-равновесных слабо изменяющихся процессов, в значительной степени отвечающих воздействию внешней среды, т.е. наличию граничных условий. Построим приближенное решение, которое по структуре отвечало разложению (3) с характерной функцией exp(-Y\[p ) и на границах временного интервала т = 0 и т = да совпадало с асимптотическими представлениями (4) и (6).

Непосредственно согласовать между собой внутреннее и внешнее асимптотические разложения для параболического оператора невозможно [2] и сконструируем мультипликатор Q , обеспечивающий гладкое сопряжение представлений (4) и (6).

В соответствии со структурой решения (3) мультипликатор построим в виде

^(т, x ) =

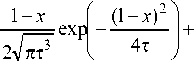
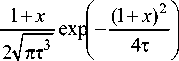
1       (  1)   (x2 -1)(2 - 3т)

—;---exp I — I -  ----p——- exp II

Vпт3     x  т^      2-Vпт7         x

. (10)

В отличие от (4), (5) приближенные представления (9), (10) работоспособны во всей области определения т и x .

Переходная функция для распределенного объекта, отвечающая постоянному входному воздействию и являющаяся интегралом от (10), описывается выражением

, , р | 1 - x |         | 1 + x

E_x ( т , x ) = erfc I —_г I + erfc I —=

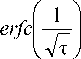
2 V пт ³

x ² - 1

-

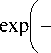
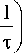
^ k ⁽ YV p ) = exp k ⁽ Y7 p ) ■ exp ^{( -}y T p ),   (8)

k zn где expk (z) = ^n=0— n-членный ряд Тейлора для exp(z).         n!

Параметры мультипликатора k и Y выби-

аппроксимирующим функцию влияния во всей области определения краевой задачи те [0, да ) , x e [0, 1] •

Полученное приближение имеет относительную погрешность менее 7% и может быть уточнено путём учёта дополнительных членов в разложениях (3) и (6).

Изложенный подход работоспособен для распределенных объектов иной формы и другими граничными условиями.

Точная передаточная функция для пластины с граничными условиями второго рода с to ₂ ( т , x ) = 5 ( т ) 5 ( x - 1) имеет вид

x ch ⁽ 4? ■ ^x ) W 2 ⁽ p , ^x ) = -/=^--/=

V psh ⁽V p )

раются из условий согласований асимптотичес-

Квазиасимптотическим решением для (12) является

ких представлений (4), (6) для различного чис-

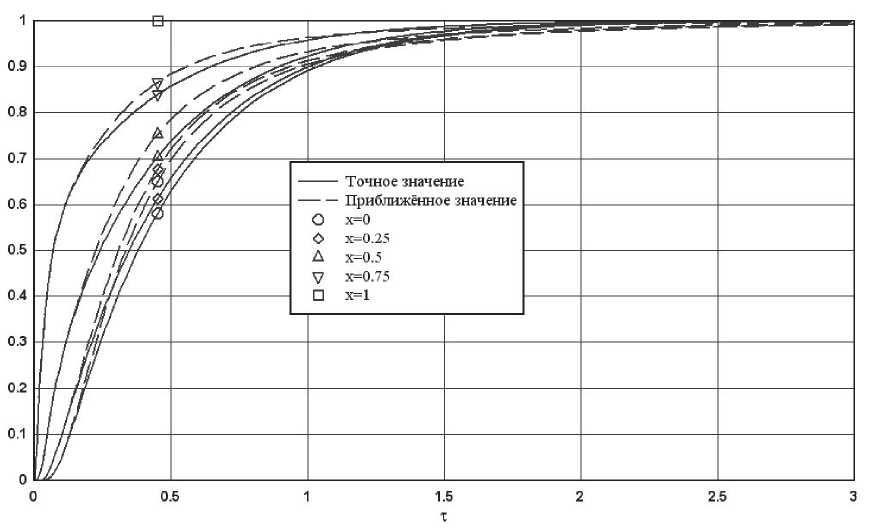
Рис. 1. Сравнение точного и приближённого (11) решений для некоторых значений координат

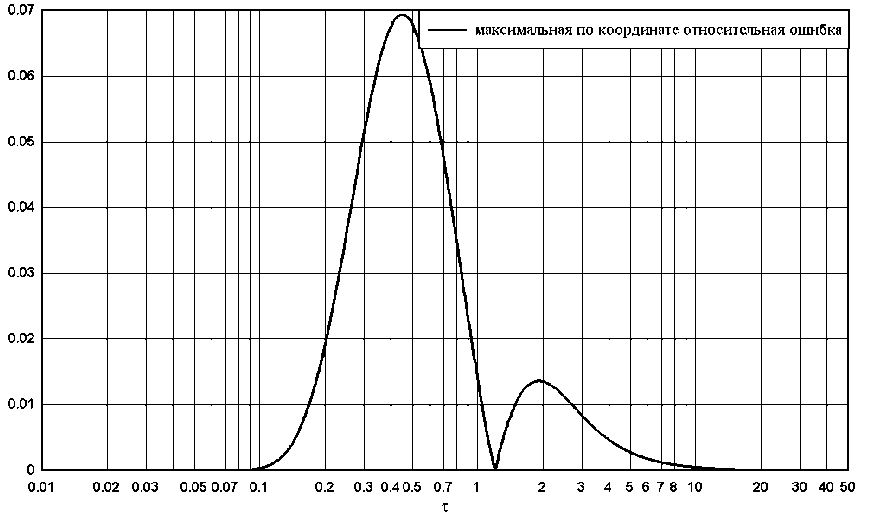
Рис. 2. Зависимость максимальной относительной ошибки приближённого решения (11) от времени

W 2 ( p , x ) = ' (^exP( ^- Vp (1 ^- x )) + ^exp^{( -} Vp (1 + x ^{)) )- p}

-

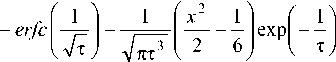
Квазиасимптотическое представление для переходной функции принимает форму

- ¹ II

6 J ))

- ¹ + p l^r

x

p

V

exp^{( - 2} 7 p ).    (13)

Приближенная импульсная переходная функция, отвечающая (13) имеет вид

E' ( t , x ) = ²V ierfc I V

-

(i - x I . a (i + x || —1=- I + ierfc |--I I +

G 2 ⁽ T , x ) =-;= exp |

-

ПТ

V

(1 — x)21 f (1 + x)2 Ц -----— I + exp| - -— I

4т  II   4тI

) V))

-

² 1 x

+ 4 т i erfc |      I +|

I                                            I

IVt ) V ²

-

1 I a i I

6 ) e* W. (15)

Приближенные конструкции (13), (14), (15) работоспособны во всей области определения

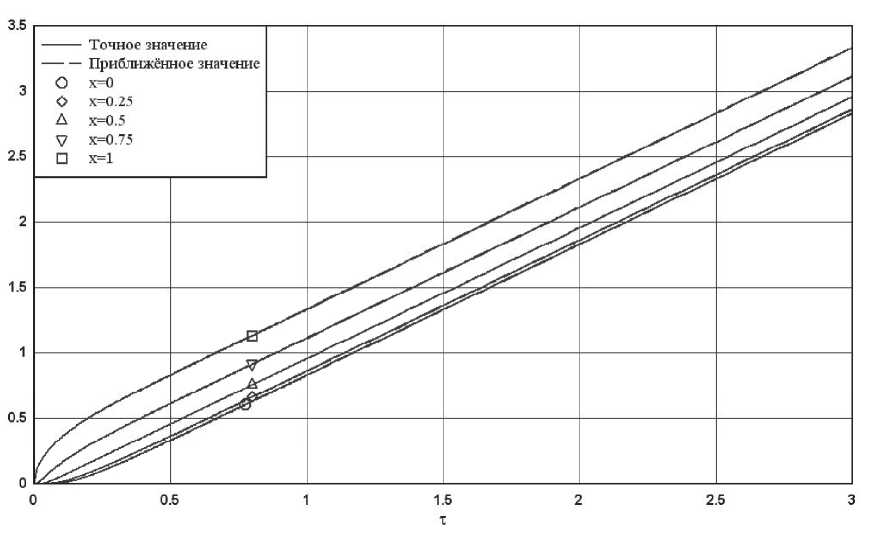
Рис. 3. Сравнение точного и приближённого (15) решений для некоторых значений координат

Рис.

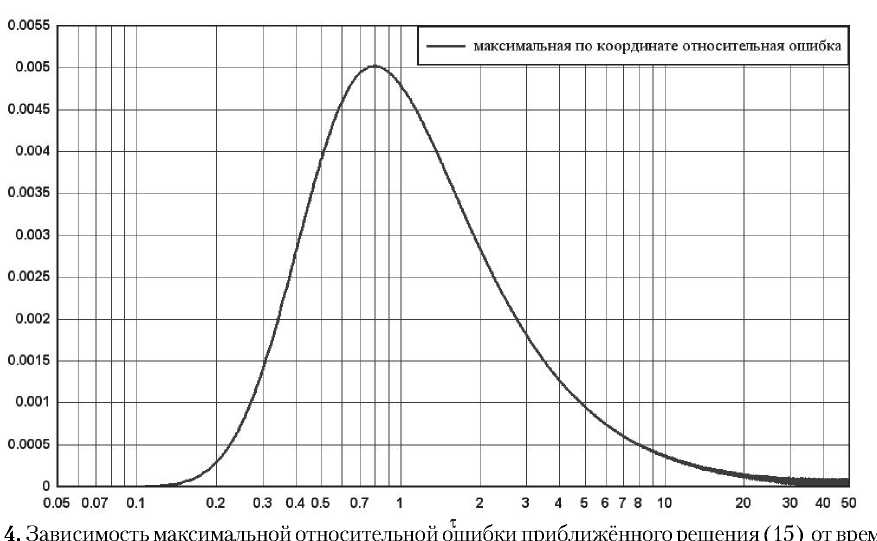
краевой задачи. Полученное квазиасимптотичес-кое представление (15) имеет относительную погрешность около 0.5%.

Для пластины с граничными условиями третьего рода точное решение для передаточной функции имеет вид

W₃ ( p , x ) = a-

ch ( Jpx )

a- ch ( 4p ) + 7 p ■ sh (7 p )

,

более сложной задачей по отношению к предыдущим примерам, поскольку в решении (16) появляется новый параметр a , вызывающий при сопряжении внешних и внутренних сингулярных асимптотических разложений дополнительные трудности.

Проводя соответствующие вычислительные процедуры, квазиасимптотическое представление для передаточной функции получим в виде

где a — безразмерный коэффициент теплоотдачи (число Био).

Построение квазиасимптотического приближенного представления для (16) является технически

W з ⁽ p , x ) = ^a T_c ■

2 ■ ch ( ^"px )

a + p"p

■ exp⁽ - ^ ) -« T c

x

(a + 2)

+

+ 2 a² x ² + 2

(a² + 2a + 2)(a + -J"p )

4-/ p       a(1 - x ²) + 1

------------------------------------------------------ • ---------:--------------------------------------

2 a + p (a + 2) a² + 2 a + 2

а(а² + 2а-2) x ² -(а³ + 4а² + 2а-4)

2--т------------

(а+2)(2а+ р(а+ 2)(а² + 2а+2)

• exp ^{- 2}T p ). (17)

Временное представление для переходной функции, отвечающее (17), имеет форму

безразмерные радиальная координата и внутренний радиус.

Квазиасимптотическими решениями для объекта (19) являются

E з ( т , x ) = erfc

1 - x )        , I 1 + x )        , | 1

---— I + erfc I ---— I - erfc I ——

2 л/ т J v 2 V t J v V t .

W 3⁽ P , x ) = RI" ^exP ^(- 7 p ⁽ r ^{- R} ) ⁾⁺

I - (1 - x ) ² 1 , - exp I -------------I erfcx

I 4 т J

-

x

—+ а 2 Vt

-

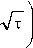
¹ - (1 + x )^{2 1} , I 1 + x 1 exp I ------------I erfcx I ---=■ + а V т I +

V 4 т J 12 Vt        J

+ 2 •

а ² x ² + 2

( а + 2 а + 2)

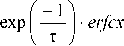
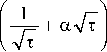
а ( а ² + 2 а- 2) x ² - ( а ³ + 4 а ² + 2 а- 4)     I- 1

------------------------------------------------------ exp I ----

( а + 2)( а ² + 2 а + 2)                V т

⁺ [ in i ^- fR I ^exp ( ^{-     (1 - 1} ) ) ,     (20)

G 3^{( т} , ^x ) ~ R¹”

( r

R )

exp

-

( r - I )²

4 т

-

-

R )

пт

exp

-

(1 - 1 )² 4 т

Полученные приближенные представления имеют замкнутую аналитическую форму, достаточную точность, элементарно вычисляются и допускают содержательный параметрический анализ.

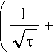
2 ат

i

\ а + 2

-

• Re erfcx

а (1 - x ²) + 1 а² + 2 а + 2

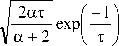
• Im erfcx I ^= + i

2 ат ¹

Работа выполнена в рамках Целевой программы “Научные и научно-педагогические кадры инновационной России на 2009-13 гг.” (государственный контракт №П1448).