Синхронизация колебаний в динамике численности двух миграционно связанных сообществ «хищник-жертва»
Автор: Курилова Е.В.
Журнал: Региональные проблемы @regionalnye-problemy
Рубрика: Региональный прогноз. Математическое моделирование
Статья в выпуске: 2 т.17, 2014 года.
Бесплатный доступ
На основе модели Базыкина разрабатывается математическая модель динамики численности двух взаимодействующих сообществ «хищник-жертва», обитающих в максимально схожих условиях и связанных между собой миграцией хищников. Проведено исследование полученной модели, определены условия синхронизации колебаний численности рассматриваемых сообществ, изучено влияние миграционного взаимодействия между сообществами на динамику каждой популяции.
Популяция, биологическое сообщество, миграция, обыкновенные дифференциальные уравнения, синхронизация
Короткий адрес: https://sciup.org/14328878
IDR: 14328878 | УДК: 517.9
Текст научной статьи Синхронизация колебаний в динамике численности двух миграционно связанных сообществ «хищник-жертва»
В современной теоретической экологии не ослабевает интерес к проблеме возникновения колебаний в динамике численности взаимодействующих популяций. Как правило, для описания динамики таких популяций используются нелинейные модели, учитывающие основные факторы их развития (рождаемость, смертность, межвидовые взаимодействия, миграция) [15]. Первые работы, посвященные изучению взаимодействующих сообществ, принадлежат Лотки и Вольтерра (Математическая теория борьбы за существование, 1931). Основная особенность этих работ состоит в том, что на основе упрощенных представлений о закономерностях развития популяций, была показана возможность возникновения закономерных колебаний численности в системе «хищник-жертва» [4]. Дальнейшее развитие модели Вольтера и Лотки шло по пути усложнения. Были предложены модификации уравнений, учитывающие различные дополнительные факторы (эффект насыщения хищника, ограниченность ресурсов жертвы и хищника даже при избытке жертвы и т.п.) [2, 9, 10, 18, 19]. Анализ таких исследований позволяет сделать вывод о том, что регулярные незатухающие колебания в системе «хищник-жертва» возникают тогда, когда численность хищника ограничивается жертвой. Если численность жертвы зависит от наличия и объема ресурсов, необходимых для жизнедеятельности, или численность хищника ограничивается не количеством жертвы, а другим фактором, то система демонстрирует затухающие колебания.
Следует отметить, что динамика численности популяций, состоящих из нескольких видов, связанных между собой трофическими взаимодействиями, весьма полно и подробно изучена (особенно системы небольшой размерности) [2, 15]. В последнее время (какпродолжение данных идей) достаточно широко изучаются задачи, посвященные исследованию закономерностей развития взаимосвязанных сообществ, каждое из которых, в частности, представляет собой автоколебательную систему [1, 7, 17, 20]. Это направление является доста точно новым, и соответственно многие аспекты динамического поведения таких систем не до конца изучены. В данной работе предлагается и исследуется модель двух взаимодействующих сообществ «хищник-жертва». В ходе исследования ее динамических режимов особое внимание уделяется изучению условий синхронизации колебаний численности между сообществами. Следует отметить, что в современной науке синхронизация преимущественно исследуется в задачах химии, физики, радиотехники [3, 5-7, 14, 17] и лишь эпизодически в биологии [8, 11, 13], особенно демэкологии [12, 16, 20].
Построение модели миграционно-связанных сообществ
В данном разделе разрабатывается математическая модель динамики численности двух связанных взаимодействующих сообществ. Предполагается, что связь между ними реализуется за счет миграции между хищниками. Каждая локальная популяция представляет собой систему «хищник-жертва» (которая в дальнейшем именуется «подсистемой»). Обозначим через х у и х у2 численность популяций жертвы и хищника в первой и второй подсистеме в момент времени t соответственно. Предполагается, что динамика каждого сообщества описывается при помощи уравнений Базыкина [2]. Следовательно, предлагаемая модель учитывает следующие факторы: нелинейный характер размножения популяции жертвы, насыщение роста хищника, внутривидовая конкуренция внутри популяции жертвы, вызванная ограниченностью ресурсов [2].
Пусть оба сообщества обитают в максимально схожих условиях, соответственно демографические параметры и коэффициенты межвидовых взаимодействий на локальном уровне в обеих подсистемах будут равными. Предполагается, что доли мигрантов относительно численности хищника из одной территории на другую также равны. Гибель особей в процессе миграции неявно включается в общую смертность. Внешние факторы, влияющие на развитие сообществ, не учитываются.
Таким образом, уравнения динамики численности двух миграционно-связанных сообществ «хищник-жертва» имеют вид:
Т2 =-су2 +"—"— + туг -ту2 1 + Лх2
где а - скорость размножения популяции жертвы в отсутствии хищника, / = а К - параметр, характеризующий внутривидовую конкуренцию жертв (самолимити-рование), b - удельная скорость потребления хищником жертвы при единичной плотности обеих популяций, с - смертность хищника d/b - коэффициент переработки потребленной хищником биомассы жертвы в собственную биомассу, А - коэффициент насыщения хищника, т - коэффициент миграции хищника.
Модель (1) содержит семь независимых параметров. После замены переменных: х = cu.(r)/d, у.= av,(т)/Ь, t=t/a, / = 1,2 приходим к системе уравнений с четырьмя коэффициентами:
-
• М1Н 2
М] = М]
-
1 + СКИ]
уи, V,
И =-№ +----+ ^2 -А1
-
1 + ски, 1(2)
. 2 V 22
М2 = W2^2
-
1 + ш/2
V2 = "AA +----- + A1 -A2
l + cm2
подстраивать свои ритмы. В связи с этим возникает ряд задач, которые требуют дополнительного исследования, а именно: возможна ли синхронизация колебаний в таких подсистемах, и если возможна, то каковы ее особенности.
Исследование синхронизации колебаний численности
В данной работе для исследования условий синхронизации колебаний двух миграционно-связанных взаимодействующих сообществ используются элементы теории синхронизации связанных нелинейных осцилляторов [1,14]. Под синхронизацией понимается максимально широкое ее значение - подстройка ритмов, которая может сопровождаться совпадением фаз, частот и амплитуд колебаний. На начальном этапе исследования рассмотрим ситуацию, когда миграционное взаимодействие между хищниками двух сообществ, обитающих на сопредельных территориях, отсутствует (параметр связи Р=О\ В этом случае система (2) состоит из двух подсистем идентичных модели Базыкина. В силу равенства коэффициентов, эти подсистемы имеют одинаковые частоты колебаний.
Модель Базыкина, описывающая подсистему «хищник-жертва», имеет три особые точки: первые две являются полутривиальными и соответствуют существованию популяции жертвы, при нулевой численности популяции хищника, третья - одновременному существованию обеих популяций [2]. На рис. 1 представлена карта типов устойчивости нетривиального равновесия уравнений Базыкина, где У.у. - устойчивый узел, Н.у. - неустойчивый узел, У.ф. - устойчивый фокус, П.ц. - предельный цикл. При а > 1-s (область Е) нетривиальная особая точка является седлом, при переходе через прямую о=1 -8 она приобретает устойчивость (области С и D). В области А рис. 1 наблюдается предельный цикл, что соответствует автоколебательному режиму модели Базыкина. В области В ненулевое равновесие неустойчиво.
Параметры системы (2) также имеют конкретный биологический смысл: 8 = Ac/d - коэффициент насыщения хищника, у= c/Kd - коэффициент самолими-тирования в популяциях жертв, р= с/а - относительная скорость роста численности хищника, равная отношению скорости гибели хищника и скорости прироста жертвы, [3=т/а - относительная доля миграции хищника, равная отношению доли мигрантов хищника и скорости прироста жертвы.
Исходя из того, что в подсистемах, описываемых моделью Базыкина, возникают флуктуации численностей обеих популяций, динамика предложенных уравнений (2) будет носить автоколебательный характер. Действительно, если сообщества изолировать друг от друга (те. 6=0), то каждое из них будет генерировать собственные колебания в ритме, который определяется свойствами подсистемы; и соответственно миграция хищников приведет к тому, что оба сообщества начнут

Рис. 1. Карта типов устойчивости нетривиального равновесия модели Базыкина
Соответственно, если система состоит из двух несвязанных сообществ типа «хищник-жертва», каждое из которых описывается моделью Базыкина [2], то ввиду отсутствия параметра связи, эти подсистемы не взаимодействуют и, как следствие, не могут подстроить свои ритмы. Следовательно, изменение частоты одной из подсистем не повлечет изменение частоты колебаний другой. Таким образом, синхронизация ритмов таких систем невозможна. С другой стороны, известно, что две связанные системы, имеющие разные периоды колебаний, подстраивают свои ритмы и начинают демонстрировать флуктуации с общим периодом. Соответственно, даже слабое взаимодействие между идентичными сообществами, отличающимися только начальным условием, способно синхронизировать их динамику [14].
Продемонстрируем наличие синхронных колебаний в системе (2). Для этого в области существования предельного цикла (область А, рис. 1а) выберем некоторую точку, например точку с координатами 6=0,12, о^0,45. Следует отметить, что коэффициент у в системе (2) не оказывает влияния на тип наблюдаемых динамических режимов, поэтому положим его равным ^0,5. Далее для этих значений коэффициентов сравним динамику двух идентичных подсистем при изменении параметра связи Р и различных начальных условиях. Выбор исходных точек итерирования осуществлялся на предельном цикле, соответствующем указанным значениям параметров, таким образом, чтобы они определяли максимальное и минимальное значения численности жертвы и, т.е.
м,(0)=0,15288^/0)=!,0802, м2(0)=6,7643, v2(0)=0,77231. Следует отметить, что все численные эксперименты, проводимые в дальнейшем, соответствуют данным начальным условиям и выбранным значениям параметров е, а и 7=0,5.
Рассмотрим ситуацию, когда сообщества слабо связаны друг с другом. В этом случае синхронизация колебаний, соответствующая совпадению значений координат фазовых точек и их одновременному движению вдоль предельного цикла, наступает спустя долгое время (рис. 2а). Так, при относительной доле миграции /7=0,005 совпадение значений численности с последующим совпадением динамики между сообществами наблюдаются через 103,5 периодов для первого и 102 периода для второго (т.е. наблюдается различная длина переходного процесса к устойчивому синхронному состоянию). Действительно, через указанное число периодов для каждого сообщества разность мгновенных амплитуд снижается до нуля, что соответствует полной взаимной синхронизации колебаний в подсистемах (рис. 2а). Таким образом, связанные сообщества в равной степени воздействуют друг на друга и взаимно подстраивают свои ритмы.
Точками на рис. 26 и 2 а представлены фазовые состояния подсистем, после которых наблюдается синхронизация их динамик. При совмещении фазовых траекторий обеих подсистем модели (2) моментальные значения численности популяций совпадают (точка на рис. 2г). Крестиками на рис. Тб-г обозначены началь-
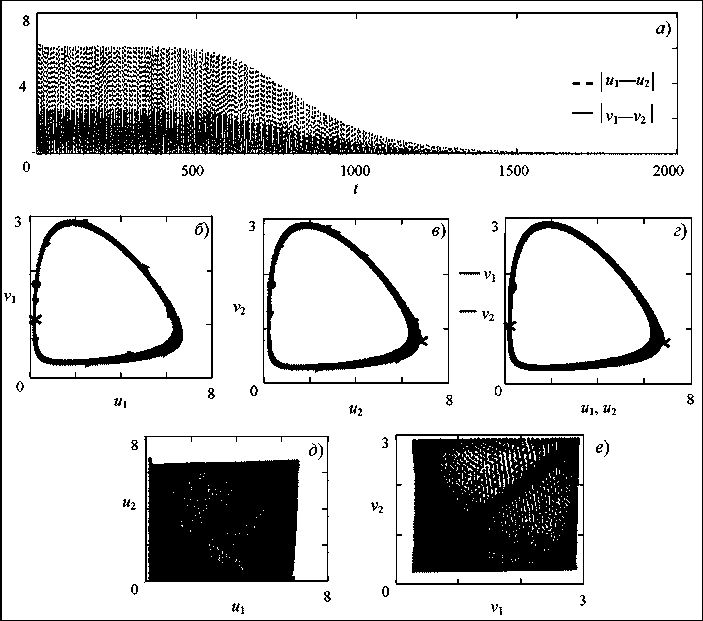
Рис. 2. Разности моментальных амплитуд (а) и двумерные проекции траекторий системы (2) при р=0,005 (б-е)
ные состояния подсистем. Стрелками указано направление движения по фазовой кривой.
Для демонстрации синхронизации динамик численности жертв в обоих сообществах была построена двумерная проекция траектории системы (2), соответствующая случаю s=0,12, 0^0,45, /=0,5, /2=0,005, на плоскости (м м) (рис. 2d). Рис. 2d демонстрирует смену асинхронных колебаний между популяциями жертвы на синхронные. Как видно, в подпространстве (ир и2) фазового пространства траектория системы (2) заполняет всю двумерную область, что указывает на асинхронный режим. Через определенное количество итераций точки траектории сливаются с биссектрисой первого координатного угла, что соответствует полной синхронизации колебаний. Динамика численности популяций хищников обоих сообществ демонстрирует аналогичный переход от асинхронных колебаний к синхронным (рис. 2е).
Далее, по аналогичной схеме был проведен ряд численных экспериментов, позволяющих исследовать возникающие динамические режимы модели (2) в зависимости от значений параметра связи. На рис. 3 представлены двумерные проекции фазового пространства системы (2), демонстрирующие связь между значениями параметра связи и скоростью перехода от асинхронного режима к синхронному (на примере популяций жертв).
На рис. 3 видно, что с увеличением значений параметра связи (относительной доли миграции Д) синхронизация наступает гораздо быстрее. Так при ^=0,05, в отличие от предыдущего случая /2=0,005, полная взаимная синхронизация колебаний численности между сообществами наблюдается через восемь периодов. При /2=0,4 не совпадающие в начальный момент времени колебания через 2 периода приходят к единой траекто рии и начинают двигаться абсолютно синхронно. Следует отметить, что /2=0,4 является бифуркационным значением, после которого рост интенсивности миграционного взаимодействия ведет к увеличению времени достижения синхронизации. Например, для /2=0,6 это время составляет 4 периода (рис. Зб-е).
Как правило, синхронизация колебаний наблюдается, когда траектории выходят на предельный цикл (рис. Зг). Однако в ряде случаев наблюдается ситуация, когда синхронизация колебаний возникает на переходном режиме, те. до выхода траектории на предельный цикл (рис. 3d).
Таким образом, проведенный анализ колебательных режимов позволяет выявить для выбранных значений параметров (^0,12, с^0,45, ;=0,5,/2=0,005) следующие закономерности синхронизации колебаний относительно интенсивности миграционного взаимодействия между сообществами: 1) при 02<0,4с увеличением значений параметра связи синхронизация наступает быстрее; 2) при /2>0,4 с ростом значений параметра связи время наступления синхронизации увеличивается.
Заключение
В данной работе исследуется математическая модель динамики численности двух связанных взаимодействующих сообществ «хищник-жертва», обитающих в максимально схожих условиях и связанных между собой миграцией хищников. Для рассмотренного примера показано, что учет миграционного взаимодействия между двумя подобными соседними сообществами приводит к синхронизации колебаний подсистем. При этом происходит как захват периода колебаний, так амплитуды и фазы. Скорость синхронизации зависит от величины коэффициента связи. Показано, что при малой интенсивности миграций для достижения полной синхрони-
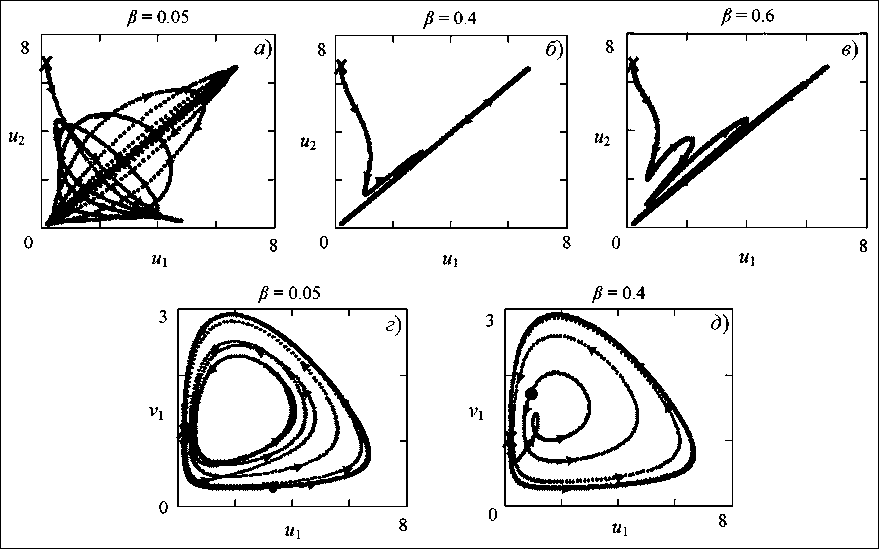
Рис. 3. Двумерные проекции траекторий системы (2) при разных значениях параметра связи
зации каждому сообществу требуется разное число популяционных циклов, что связано с первоначальным различием в длинах периодов колебаний изолированных систем. Очень сильная связь стремится сделать состояния обоих осцилляторов идентичными. Обнаружено, что для выбранных значений коэффициентов существует некоторое бифуркационное значение параметра, характеризующего миграционное взаимодействие, при котором синхронизация наступает максимально быстро. Показано, что переход через это значение ведет к увеличению числа периодов достижения синхронизации.
Список литературы Синхронизация колебаний в динамике численности двух миграционно связанных сообществ «хищник-жертва»
- Анищенко В.С., Астахов С.В., Вадивасова Т.Е., Феоктистов А.В. Численное и экспериментальное исследование внешней синхронизации двух частотных колебаний//Нелинейная динамика. 2009. Т. 5, № 2. С. 237-252.
- Базыкин А.Д. Математическая биофизика взаимодействующих популяций. М.: Наука, 1985. 181с.
- Блехман И.И. Вибрационная механика. М.: Физматлит, 1994. 400 с.
- Вольтерра В. Математическая теория борьбы за существование. М.: Наука, 1976. 288 с.
- Жаботинский А.М. Концентрационные автоколебания. М.: Наука, 1974. 179 с.
- Колесов А.Ю. Специфические релаксационные циклы сингулярно-возмущенных систем типа Лотки-Вольтерра//Изд. АН СССР, Сер. матем. 1991. Т. 55. С. 515-536.
- Кузнецов А.П., Сатаев И.Р., Тюрюкина Л.В. Синхронизация и многочастотные колебания в цепочке фазовых осцилляторов//Нелинейная динамика. 2010. Т. 6, № 4. С. 693-717.
- Кулаков М.П., Аксенович Т.И., Фрисман Е.Я. Подходы к описанию пространственной динамики миграционно-связанных популяций: анализ синхронизации циклов//Региональные проблемы. 2013. Т. 16, № 1. С. 5-14.
- Курилова Е.В., Кулаков М.П., Хавинсон М.Ю., Фрисман Е.Я. Моделирование динамики добычи минеральных ресурсов в регионе: эконофизический подход//Информатика и системы управления. 2012. Т. 34, № 4. С.3-13.
- Курилова Е.В., Кулаков М.П. Условия синхронизации численности двух взаимосвязанных сообществ (на основе модели Лотки-Вольтерра)//Региональные проблемы. 2014. Т. 17, № 1. С. 5-8.
- Лаптев М.В. Компьютерное моделирование взаимной синхронизации автоколебаний клеточной плотности гиперпролиферирующего эпидермиса в патогенезе псориаза//Клиническая медицина. 2012. № 2. С. 97-102.
- Наумов Н.П. Географическая изменчивость динамики численности и эволюция//Журн. общей биол. 2000. Т.61, № 5. С. 535-549.
- Павлов Е.А., Осипов Г.В. Синхронизация и хаос в сетях связанных отображений в приложении к моделированию сердечной динамики//Компьютерные исследования и моделирование. 2011. Т. 3, № 4. С. 439-453.
- Пиковский А., Розенблюм М., Куртс Ю., Синхронизация. Фундаментальное нелинейное явление: Пер. с англ. А.С. Пиковского, М.Г.Розенблюма. М.: ТЕХНОСФЕРА. 2003. 496 с.
- Ризниченко Г.Ю. Математические модели в биофизике и экологии. Москва-Ижевск: ИКИ. 2003. 184 с.
- Садовский М.Г. Модель «хищник-жертва», в которой особи совершают целенаправленные перемещения по пространству//Журнал общей биологии 2001. Т. 62, № 3. С. 239-246.
- Abta R., Schiffer M., Ben-Ishay A., Shnerb M.N. Stabilization of metapopulation cycles: Toward a classification scheme//Theoretical Population Biology. 2008. Vol. 74. p. 273-282.
- Hoiling C.S. The functional response of predetory to prey density and its role in mimcry and pulution regulation//Mem. Entomol. Soc. Canada. 1965. No. 45. p. 1-60.
- Rosenzweig M.L., Mac Artur R.H. Graf ical representation and stability conditions of predatory-prey interactions//Amer. Natur. 1963. Vol. 97. No. 893. p. 209-223.
- Moitri Sen, M. Benerjee, A. Morozov. Bifurcation analysis of a ratio-dependent prey-predator model with the Allee effect//Ecological Complexity. 2012. No. 11. p. 12-27.


