Синхронная квазитрехмерная (Q3D) секционная модель динамики биомассы сообщества деревьев

В работах [1, 2, 3] представлены двумерные модели растения и сообщества растений и некоторые результаты их анализа и применения. Эти модели показали свою адекватность при анализе «правила - 3/2» [4] и эффекта не монотонности динамики конкуренции в однородных сообществах деревьев [5, 6]. Однако при качественно соответствующем сути дела поведении количественные модельные результаты в некоторых случаях заметно отличаются от реальных. Это может быть связано с несоответствием трехмерного объекта и его двумерного представления. Ниже кратко описан подход к трехмерному моделированию динамики биомассы дерева и конкуренции в сообществе деревьев, исходящий из принципа «минимального угла зрения» [7].

СЕКЦИОННАЯ МОДЕЛЬ СВОБОДНО РАСТУЩЕГО ДЕРЕВА

На примере ели вводится в рассмотрение элемент архитектуры дерева секция - стволовые мутовка с ветвями и междоузлие и, тем самым, выделяется секционная структура дерева [8, 9] (см. также [10]). Это дает возможность разложить известную динамику B ( T) биомассы¹ всего дерева в распределенную по высоте дерева систему динамик b ( T) биомасс составляющих дерево секций ( T - возраст всего дерева). Динамика i -секции (акропетально - i = 0,1,2,...) начинается с появления на макушке дерева почки, дающей начало секционному осевому междоузлию, которое растет в высоту в течение сезона. В следующем сезоне ситуация повторяется для ( i +1)-секции.

Рассмотрим соотношение между биомасса- ми реальной i-секции дерева и целого дерева, используя образ виртуального i-дерева. В момент Ti инициирования каждой новой i-секции дерево начинает реализовывать новую виртуальную динамику Bi(T-Ti) биомассы виртуального дерева - верхней части всего дерева, начинающейся с этой i-секции (B.(x) = 0 приx = T-Ti J 0). С нулевой секции начинает реализовываться виртуальная динамика биомассы виртуального 0-дерева, которая совпадает с реальной: B0(T) = B(T). В момент T,+1 появляется следующее виртуальное (i +1) - дерево, вложенное в предыдущие виртуальные деревья. Биомасса реальной i-секции есть разность биомасс виртуальных i- и (i +1)-деревь-ев b=Bi(T —_;)- Bi+1(T - T-AT Хщ) где AT - временной шаг появления секций.

Предполагая функции B i ( x ) монотонными и ограниченными ( ст - функции²) можно получить ряд интересных (и реальных) свойств динамики биомассы секции. Модельный результат И.А. Полетаева [11] показывает, что рост дерева в высоту ограничен и может быть описан выражением

H(T ) = H m tanh( T / A 2 ) .             (2)

Согласно этому, в двумерных моделях [1,3] биомасса свободно растущего дерева описывается как заданная на всей положительной полуоси

B (D = B„ tanh — (T / A),       _ _ (3 _ где tanh(x) - тангенс гиперболический; A 1, Bm, A2, Hm - размерные параметры, — - аллометрический показатель, в случае изометрии равный 3. Рисунок 1 представляет нормированные на максимальные значения зависимости H(T) и B(T) при A 1 = A2 и — = 3. Для описания динамики биомассы Bi (T-Ti) виртуального i-дерева выражение, подобное выражению (3), используется далее с за- меной параметра Bm на Bm i. Из процедуры получения выражения (1) следует, что конкретный вид функции B(T) не существенен.

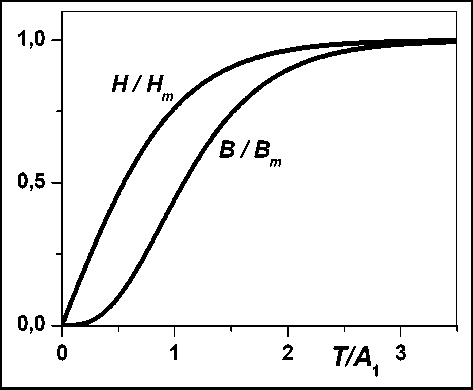
Рис. 1. Динамика высоты дерева и его биомассы

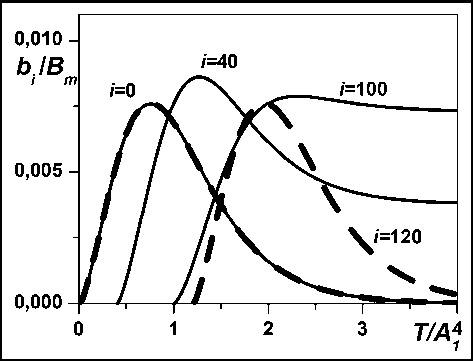
Рис. 2. Динамика биомассы секций.

Акропетальное оголение ствола. Из выражения (1) и предположения об идентичности о - образных динамик B i ( T-T_i ) виртуальных деревьев следует, что динамика биомассы секции имеет колоколообразную форму, т.е. качественно отличается динамики для дерева. Из этого следует, что биомасса секций с возрастом акропе-тально оголяется, что действительно имеет место для многих видов деревьев. Колоколообразная форма динамики суммарной массы хвои ветви ели (и, следовательно, яруса из примерно пяти ветвей и соответствующей секции) была продемонстрирована с использованием метода возрастных рядов по натурным данным в работе [12]. На рис. 2 (штриховые линии) представлена динамика биомассы, вычисленная с использованием (1) и (4) для нескольких секций.

Невозможность о - образной динамики фитомассы. Ограниченность или неограниченность динамики биомассы и фитомассы дерева при T ^ж не могут быть показаны непосредственно натурным наблюдением. Как известно, биомасса B ( T ) является источником фитомассы P ( T) растения и, следовательно, в рамках детальности используемой модели дерева всю накопленную на момент T растением фитомассу можно описать неким интегралом от B ( T ) в пределах от 0 до T . Предполагая, что интенсивность производства биомассой фитомассы не слишком быстро уменьшается с возрастом и учитывая о -образность функции B ( T ), можно заключить, что рост фитомассы дерева неограничен. Биологические аргументы для такого вывода смотри в работах [13, с. 9;14, с. 55].

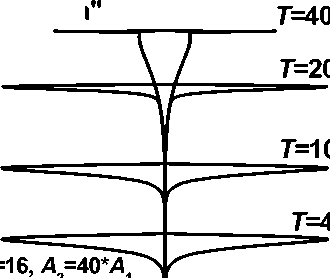
Предельная форма свободно растущего дерева. При идентичности динамик B i ( x ) виртуальных деревьев, означающей отсутствие зависимости виртуальной биомассы деревьев от высоты (от номера секции - меры высоты положения секции), предельная форма есть небольшое число (одна в пределе) живых секций (которые имеют существенную биомассу) на вершине дерева, занимающего область свободного роста - круг, т. е. нечто подобное зонтику. На рис. 3 представлена динамика распределений биомассы секций по высоте свободно растущего дерева для нескольких возрастов T . Некоторые формы деревьев, например, в саванне указывают, что этот эффект можно встретить в реальности (см. также [10, fig.22, p. 391];13, рис. 177, 187, с. 287,300]).

Распределение биомассы по секциям. Наблюдения форм деревьев многих лиственных (и не только) видов деревьев зрелого возраста показывают, что акропетальное оголение ствола значительно замедляется, если не заканчивается на некоторой высоте (в отличие от идеального случая, рис. 3). Это значит, что динамика биомассы секций с большим номером i (большей высотой возникновения) , возможно сохраняя «колоколообразную» форму, не обязательно стремится к нулю с увеличением возраста секции (рис. 2, сплошные). Для этого достаточно, чтобы величина B m _i в выражении (4) зависела бы некоторым образом от высоты H i появления соответствующего виртуального i- дерева:

BAT , H i ) = в , ,( ^H i ^)tanh ' (Т / 4).

При этом следует заметить, что зависимость биомассы Bi(TH) виртуального i-дерева от высоты Hi не отражается в заданной зависимости биомассы B(T) всего реального дерева. Очевидно, что из (1) и (4) следует B.(TH) > Bi+1(TH+1). Это соотношение следует также из физических соображений [11]. Можно предположить, что тип зависимости

B m ⁽ H> = M , ( x ), x = H i / H m ,       5)

который определяет форму распределения биомассы по секциям, может быть специфичным для биоморф деревьев. Функции f₀ ( x ) должны быть невозрастающими и уменьшаться от 1 в точке x = 0 до 0 в x = 1.

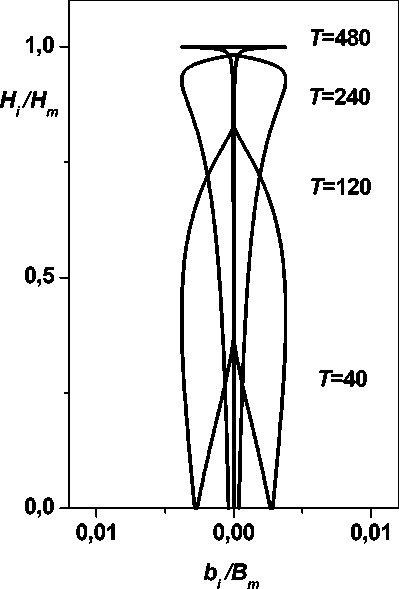
Рис. 3. Образование «зонтикообразной» формы дерева примера распределения биомассы дерева по высоте (f, (x) = (1 - x)r), иллюстрирующие сказанное (более подробно см. [10]).

СЕКЦИОННАЯ МОДЕЛЬ ДЕРЕВА, РАСТУЩЕГО НЕ СВОБОДНО

Как и в двумерном случае [1, 2, 3], площадь территории, доступной дереву в сообществе, принимаем как меру доступных дереву ресурсов. Свяжем азимутальную структуру биомассы дерева и секций с формой и размером территории, на которой дерево растет. Свободно растущее дерево, очевидно, имеет годограф азимутального распределения биомассы в форме круга увеличивающегося с возрастом радиуса. Вполне естественно предположить, что если по какому-то азимуту форма территории не обеспечивает выполнение условий свободного роста, то для этого азимута рост биомассы будет замедляться и, вообще говоря, соответствующая часть биомассы начнет отмирать. Натурные наблюдения над соседними деревьями показывают, что нижние соприкасающиеся части крон между ними растут гораздо слабее, чем в противоположных направлениях, а рост верхних, вообще говоря, не зависит от азимута. Такое различие ситуаций с нижними и верхними частями кроны определяет необходимость использования трехмерных моделей конкуренции в сообществе.

Секция и секторы. Дерево в сообществе и составляющие его секции используют ресурсы и растут на части территории сообщества - полигоне Вороного (рис. 5, штриховая линия). Разобьем круг свободного роста (угол 2 п ) и, соот-

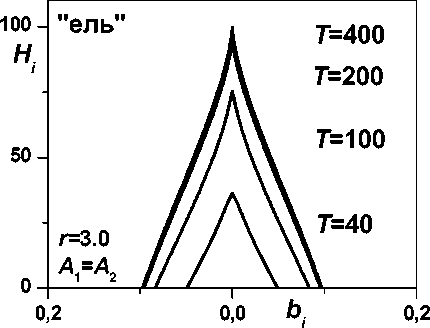
100 ʺпальма

H

i

0,2

0,0         b_i   0,2

Рис. 4. Динамика распределения биомассы дерева по высоте (по секциям)

Другим источником разнообразия распределений биомассы дерева по секциям (по высоте) в рамках данной модели является соотношение масштабов времени A 1 и A2 динамики биомассы и высоты в (1) и (2). На рис. 4 представлены два ветственно, полигон на ns одинаковых секторов и к каждому j-му сектору i-й секции применим с соответствующими изменениями уравнение, использованное при двумерном моделировании динамики биомассы дерева [3]:

db . dT = k( T - T )( b j I т( B , T ) + J/b . I b F ,. db F l dT ) - b . l т( B , T ) , (6) k ( T - T ) = min(1, a. , j (T - T )l a Fi ,j (T - T )) , (7) т ^-1 ( B , T ) = (aB^{k -1} + т ^-1)l(1 + C g (1 - k ( T - T ))) , (8)

f(b -V b F. = ( b i. I b_F j ^Y l(1 + c_G (1 - k ( T - где a. . ( T - Ti ) и a Fi ( T площадь пересечения j -сектора полигона с кругом свободного роста и площадь, необходимая для свободного роста в возрасте T дерева соответственно, b ( T - Ti ) и b Fi ( T - Ti ) биомасса данного сектора и свободно растущего сектора, a B k ^{- 1} удельные затраты на основной обмен биомассы B дерева (0 <  к < 1),

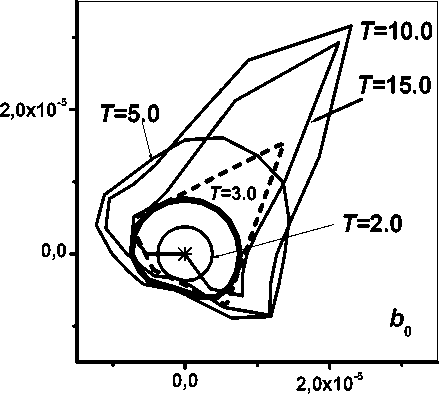
Рис. 5. Полигон и динамика годографов биомассы 0-секции.

T ))) , (9)

1l т_м удельная интенсивность производства фитомассы биомассой, c_G коэффициент дыхания роста [15], функция f ( x ) существенна при возобновлении роста растения (0 <  у <  1). На рис. 5 представлена динамика годографов биомассы 0-секции дерева, растущего на полигоне.

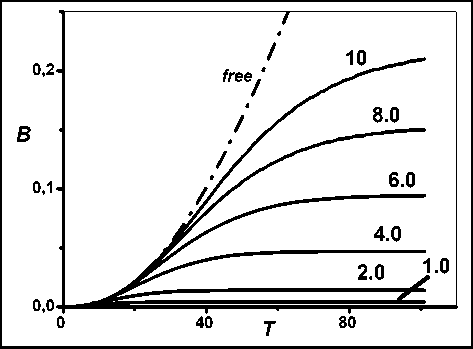
Pиc. 6. Динамика биомассы дерева для полигона разной площади

СИНХРОННАЯ МОДЕЛЬ ДИНАМИКИ СООБЩЕСТВА ДЕРЕВЬЕВ

На рис. 6 приведены модельные динамики биомассы дерева, растущего на полигоне, изображенном на рис. 5, при различных значениях масштабного коэффициента k s (разных значениях площади полигона). В отличие от двумерной модели, секционная модель дерева показывает, что дерево, растущее на полигоне любой площади (рост «в цилиндре»), не отмирает и его биомасса выходит на стационарное значение, определяемое имеющейся площадью роста. Механика этого достаточно очевидна: секции нижней части кроны, последовательно достигающие предела площади полигона, со временем отмирают, но зато появляются свободно растущие секции в верхней части кроны. Этот существенный вывод указывает на то, что деревья в сообществе отмирают (сообщество изреживается) не непосредственно из-за недостатка площади (ресурсов), а из-за того, что недостаточность ресурсов приводит к уменьшению скорости роста дерева в высоту. Более подробно результаты данного раздела рассматриваются в [16].

Алгоритм квазитрехмерной синхронной модели сообщества деревьев, как и в случае двумерной модели состоит в следующем. На территории сообщества исходно по некоторой схеме размещаются модели деревьев. Каждому дереву путем построения мозаики Вороного ставится в соответствие часть территории (и соответствующие ресурсы). Каждое дерево развивается в соответствии с площадью территории, которой оно обладает, и явным образом не взаимодействует с соседями. Если в некоторый момент этой территории (ресурсов) стало недостаточно, то дерево начинает отмирать и при выполнении соответствующего условия оно считается отмершим. После отмирания дерева занимавшаяся им территория подлежит разделу по некоторым правилам между его соседями, что и является, собственно, явным взаимодействием деревьев в модельном сообществе. Соседи отмершего дерева, получив прибавку территории, могут, если они тоже находились на стадии отмирания, изменить свои намерения и продолжить рост.

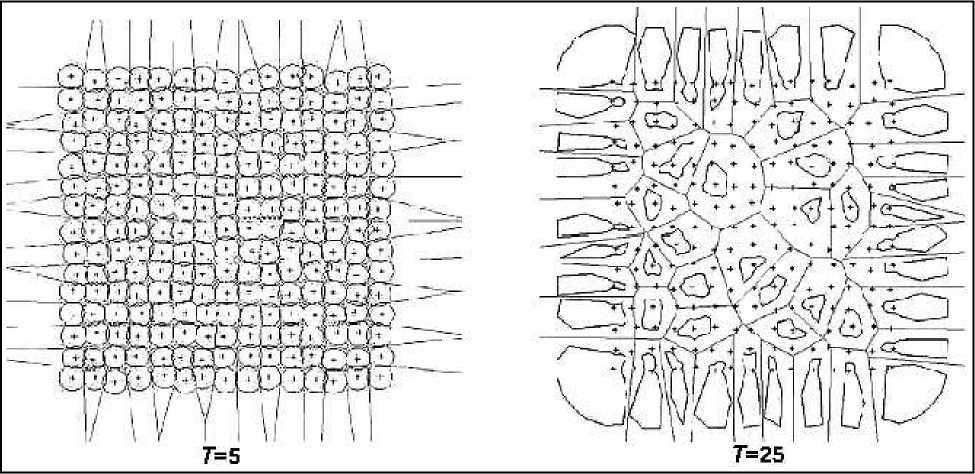
Рис. 7. Динамика мозаики Вороного и системы годографов биомасс деревьев в ходе изреживания сообщества

Очевидно, что в действительности члены сообщества взаимодействуют при использовании ресурсов не только в трагические моменты, но и в промежутках между ними. Поскольку, разделив между деревьями территорию сообщества, мы уже используем двумерные оценки ресурсов, приходящихся на дерево в сообществе, и соответствующий механизм взаимодействия функционирует во времени точечно и радикально, то для непрерывного во времени взаимодействия деревьев остается лишь взаимодействие в третьем измерении, т.е. в ходе роста в высоту (подробнее см. [17]).

На рис. 7 представлены для двух моментов времени мозаики Вороного и годографы биомасс деревьев однородного сообщества [5, 6]. В качестве критерия отмирания дерева использовалось соотношение B_i ≤ ε _MB_{n , i} , где B_i - биомасса i- го дерева, B_n,i - величина средней биомассы деревьев, соседних по полигону Вороного к фокальному i- тому дереву, параметр ε _M <  1 . Подобные эмпирические соотношения разной степени громоздкости между характеристиками фокального дерева и его соседей используются в качестве индексов конкуренции во многих работах по эмпирическому анализу влияния окружения дерева на его рост [18].

ЗАКЛЮЧЕНИЕ

Таким образом, трехмерные модели конкуренции должны отличаться от двумерных именно учетом различий в росте деревьев в высоту, связанных с различием в обеспечении их территорией (ресурсом). Очевидно, что различие в ско- рости роста соседних деревьев должно приводить со временем к пространственной «десинхронизации» одновозрастных секций соседних деревьев и, соответственно, к необходимости поиска способов учета этого процесса в модели динамики биомассы дерева.

Работа выполнена при поддержке гранта РФФИ (№ 06-04-49366).