Синхронный гидромеханический привод рабочего органа мобильной машины и его математическая модель

Введение. Технологические машины, как мобильные, так и стационарные, зачастую содержат синхронные гидромеханические приводы, в которых необходимо обеспечить работу двух или более гидравлических двигателей, запитываемых от одного источника расхода — насоса, гидроаккумулятора и др. Как показали ранее проведённые исследования, решение подобных задач проще всего осуществлять с использованием дроссельных делителей потока [1].

Настоящая работа посвящена исследованиям синхронного гидромеханического привода мобильной технологической машины на примере привода щётки аэродромной уборочной машины на базе дроссельного делителя потока незолотникового типа.

Объект исследования. На рисунке 1 приведена схема синхронного гидромеханического привода щётки уборочной машины. Он включает в себя дизельный двигатель внутреннего сгорания (ДВС), гидравлические насосы Н1 и Н2, установленные на общем валу с возможностью параллельной работы, два гидромотора М1 и М2, также включённых параллельно и приводящих в движение вал барабанного щёточного устройства (далее — щётка) через цепные передачи ЦП1 и ЦП2.

Проведённые ранее исследования аэродромной уборочной машины [2], показали, что механическая система машины не оказывает существенного влияния на работу привода щётки. В результате исследований были получены параметры системы привода щётки, обеспечивающие её работу в оптимальном режиме и доказана целесообразность применения дроссельной синхронизации работы гидравлических моторов в системе привода щётки [3]. Однако, предложенный ранее для этой цели дроссельный делитель потока мембранного типа [4] не вполне удовлетворяет условиям эксплуатации большинства мобильных машин вообще и аэродромной уборочной машины в частности.

Учитывая, что аэродромная уборочная машина работает в зимний период при достаточно низких температурах, авторы предлагают применить в её схеме, взамен мембранного, незолотниковый дроссельный делитель потока с задатчиком плунжерного типа (см. рис. 1).

К системам управления гидроцилиндрами

М3

ДП

КП

Р2 b

3 b mF

2 a

1V

---ir

Н1

КП1

M „ a 5

КП2

Зв 1.1       16

ЦП1

Зв 1.2

Н2

'        17

ЩЁТКА

Мн

Зв 2.1

ЦП

Зв 2.2

-e-

КП4

М2

«—

о 23

Др )

-t । 27

Ф

Рис. 1. Расчётная схема системы привода щётки уборочной машины

При этом вся система гидравлического привода щётки условно может быть разделена на три подсистемы:

• -    первая включает в себя источник питания и аппараты управления (от ДВС до точки 7 гидравлической системы);

• -    вторая объединяет силовой контур (гидромоторы, механическую передачу и непосредственно исполнительный орган — щётку);

• -    третья представляет собой незолотниковый дроссельный делитель потока с задатчиком плунжерноготипаДП.

На рисунке 2 изображена подсистема синхронизации привода щётки уборочной машины, представляющая собой дроссельный делитель потока незолотникового типа, работа которого осуществляется следующим образом. Если нагрузки в синхронизируемых ветвях одинаковы, то расходы рабочей жидкости через входные сопротивления (чувствительные элементы) 3 и 5 одинаковы, а следовательно, одинаковы и потери давления на них. Тогда давления в камерах управления 2 и 6 отличаются на одну и ту же величину от давлений в соответствующих им вспомогательных камерах 1 и 7. Так как диаметры плунжеров 14 и 9 одинаковы, то одинаковы и их эффективные площади, следовательно, и усилия от перепада давлений на них, передаваемые подвижному штоку переменного сечения 4, будут также одинаковыми. Но эти усилия направлены в противоположные стороны, а потому регулирующий элемент останется неподвижным, а потери давления на переменных гидравлических сопротивлениях типа плоский клапан 13 и 10 равными.

Если на одном из гидромоторов, например на гидромоторе МН2, подсоединённом к выходному отверстию 11, нагрузка станет больше, чем на гидромоторе МН1, подсоединённом к выходному отверстию 12, то расходы в этой ветвии через входное сопротивление 5 уменьшатся. Соответственно, уменьшится и перепад давления на этом сопротивлении. В результате сила действия перепада давления на плунжер 9 станет меньше, чем на плунжер 14, что приведёт к перемещению штока переменного сечения 4 вместе с регулирующим элементом в сторону закрытия переменного гидравлического сопротивления 13. Его сопротивление увеличится, и расходы в ветвях, а следовательно, и скорости вращения валов гидромоторов выровняются.

1         2 3      4

5   6     7

11    10

Рис. 2. Дроссельный делитель потока незолотникового типа, как подсистема синхронизации привода щётки уборочной машины

Математическая модель системы привода. Моделирование системы привода щётки будем осуществлять способом, предложенным в работе [5], согласно которому вся гидравлическая система привода разбивается узловыми точками на участки, для каждого из которых выполняется условие dpi                          , dt пр вх вых , где dpi — приращение давления в i-й точке рассматриваемой гидравлической системы за время dt; Спр — коэффициент приведённой объёмной жёсткости соответствующего участка гидравлической системы; £ QBX — сумма всех расходов рабочей жидкости поступающих в рассмат риваемый объём системы за время dt £ Qвых — сумма всех расходов рабочей жидкости от- водимых из рассматриваемого объёма системы за то же время.

Расходы рабочей жидкости через местные гидравлические сопротивления, входящие в уравнения приращения давлений, определяются с учётом свойств гидромагистралей и гидравлических аппаратов по формуле

Q = Voonp ■ Fconp ^Р ■ рвх - РвыД ■ Sign (Рвх - Рвых ) , где μсопр — коэффициент расхода соответствующего гидравлического сопротивления; Fсопр — площадь его живого сечения; pвх и pвых — соответственно давления рабочей жидкости на входе и выходе рассчитываемого гидравлического сопротивления; ρ — плотность рабочей жидкости.

Коэффициенты расхода линейных гидравлических сопротивлений в предложенном уравнении определим по формуле

μ сопр

μ тр . пр

1 + тр

l тр d тр

где μтр.пр — мгновенное значение коэффициента расхода участка трубопровода или канала круглого сечения; λтр — мгновенное значение коэффициента трения соответствующего участка трубопровода или канала круглого сечения; lтр иdтр — соответственно длина и диаметр рассматриваемого участка трубопровода или канала круглого сечения.

Скорость движения регулирующего элемента делителя потока (штока 4 совместно с плунжерами 15 и 9) определим из уравнения его движения. Мгновенные значения расходов рабочей жидкости через гидравлические машины, входящие в уравнения расчёта приращения давлений, рассчитаем с учётом свойств гидравлической машины по формулам:

^Q g.M1;д.М 2              "  w M1;M 2 "  ^ 3в 1.1; 3в 2.1 ,

η о . М 1,2

^Qg.H1;д.Н 2 = ^П о . Н 1; о.Н 2 "  w H 1; Н 2 "  ^№ ДВС ,

^QBCH 2 = ^WH 2 "  ™ ДВС ,

η о . ГМ

= ¹ - 1 ¹ - П _О . Мном ) "

pГМ ном.ГМ

где Qд.М1, Qд.М2 — действительные расходы рабочей жидкости, проходящие через соответствующие гидромоторы; Qд.Н1, Qд.Н2 — действительные расходы рабочей жидкости, проходящие через гидронасосы Н1 и Н2; wМ1;М2 и wН1;Н2 — характерные объёмы соответствующих гидромоторов и гидронасосов; ηо.М1, ηо.М2 и ηо.Н1, ηо.Н2 — объёмные коэффициенты полезного действия соответствующих гидромоторов и гидронасосов; ηо.ГМ — текущее значение объёмного коэффициента полезного действия соответствующей гидромашины (насоса или мотора); ηо.ГМ.ном — номинальное значение объёмного коэффициента полезного действия соответствующей гидромашины (принимается равным объёмному коэффициенту полезного действия гидромашины при номинальном давлении); pном.ГМ — номинальное давлении соответствующей гидромашины; pГМ — текущее значение перепада давления на соответствующей гидромашине; ωЗв1.1, ωЗв2.1 — угловые скорости вращения звёздочек непосредственно установленных на валы соот- ветствующих гидромоторов, скорости вращения которых определятся по уравнениям:

^№ М1 = 1     ^{( М} М1   ^М Зв11 ) ,

J прМ 1

^№ М 2 = 1    ^(М М 2    М Зв 2.1 ) ,

J прМ 2

^ММ 1 = ^WM1 ( p 20 - p 18 ) "  ^П мМ1 ,

^ММ 2 = w M 2 ( p 21 - p 19 ) "  ^П мМ 2 ,

ω Зв 1.2

J прЗв .1.2

П _Ц 1 "  — М з _В 11 - Мщ12

V * ЦП

ω Зв 2 2

J прЗв 2 2

Г

П ц 2

V

•     ‘ ‘ Зв 2.1

ц п

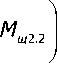
М + М М

^МЩ1 ^{+ м}щ 2 ^мщ ,

Мщ = M + ф " № щ , где ωМ1, ωМ2 — угловые скорости вращения валов соответствующих гидромоторов; MМ1 и MМ2 — крутящие моменты, развиваемые соответствующими гидромоторами; MЗв1 1 и MЗв2 1 — моменты сопротивления вращению валов гидромоторов со стороны соответствующих звёздочек; JпрМ1 и JпрМ2 — моменты инерции подвижных частей, приведённые к валам соответствующих гидромоторов; JпрЗв 1 2 и JпрЗв2 2 — моменты инерции подвижных частей, приведённые к валам соответствующих звёздочек; ηц1;ц2 и iц п — коэффициенты полезного действия соответствующих цепных передач и их передаточное число; Mщ1.2 и Mщ2.2– моменты сопротивления вращению со стороны щётки, приведённые к валам звёздочек 1.2 и 2.2; МЩ — полный момент сопротивления вращению щётки со стороны очищаемой поверхности; М — постоянная составляющая момента сопротивления вращению щётки; ψ — коэффициент пропорциональности, определяется экспериментально [6]; ωЗв1.2 и ωЗв2.2 — угловые скорости вращения звёздочек 1.2 и 2.2 непосредственно установленных на валу барабана щёточного устройства.

Соотношение между М щ1 и М щ 2 зависит от состояния бетонного покрытия и снежноледяного покрова очищаемой поверхности.

Динамика работы подсистемы синхронизации — дроссельного делителя потока незолотникового типа с переменными гидравлическими сопротивлениями типа плоский клапан и задатчиком плунжерного типа может быть описана с использованием той же методики — по приращениям давления рабочей жидкости в различных точках делителя потока по мере её продвижения по делителю потока. Определим указанные приращения давлений из предположения, что регулирующий элемент перемещается в право — в сторону прикрытия переменного гидравлического сопротивления 13, что соответствует случаю увеличения нагрузки на гидромоторе М2, по уравнениям:

Р7 = Спр7 (^6-7 — Q7-8 — Q7-9 — Q06BI + Q06B2 ) , p10,11

p 8,9    ^Спр 8,9 ^{( Q} 7 — 8,7 — 9

—

Q 41,2 ) ,

= С пр10,11 ( Q 412 ± Q_m 1,2 + Q щ12

—

Q рег 1 2

^Qotb1, 2 ) ,

p 12,13    ^Спр12, 13 ⁽ ± ^Qo6b 1, 2 ^{+ Q}пл1, 2 ) ,

•

p 14.15

= c пр14,15

^{( Q}рer 1,2

—

Q вых.1,2

± ^Qotb 1,2 ) ,

•

p 16,17

^Спр 16,17 ^{( Q}вых .1,2

—

Q 16-18,17-19

),

•

p 18,19

^Спр 18,19 ^{( Q} 16-18,17-19

—

^QM1, М 2 ) ,

•

p 20,21

^Спр 20,21 ⁽ Q M 1, М "2

—

Q 20-22,21-22

) ,

где p 7 … p 21 — величины давления в соответствующих точках расчётной схемы; С пр 7 … С пр 21 — коэффициенты приведённой объёмной жёсткости соответствующих участков расчётной схемы; Q 7-8 , Q 7-9 , Q 16-18 , Q 17-19 , Q 20-22 и Q 21-22 , — расходы рабочей жидкости на соответствующих участках гидравлической системы; Q обв 1 и Q обв 2 — расходы рабочей жидкости через обводные каналы соответствующих ветвей ДП, вызванные перемещением его регулирующего элемента; Q ч 1 и Q ч 2 — расходы рабочей жидкости через соответствующие чувствительные элементы, делителя потока; Q пл 1 и Q пл 2 — расходы рабочей жидкости, вызываемые перемещением плунжеров (14 и 9) соответствующих ветвей регулирующего элемента ДП; Q щ 1 и Q щ 2 — расходы рабочей жидкости через кольцевые щелевые зазоры между плунжером и корпусом соответствующей ветви делителя потока ДП; Q pег 1 и Q рег 2 — расходы рабочей жидкости через переменные сопротивления регулятора соответствующих ветвей ДП; Q вых 1 и Q вых 2 — расходы рабочей жидкости через выходные каналы соответствующих ветвей ДП; Q отв 1 и Q отв 2 — расходы рабочей жидкости через дожимные отверстия 15 и 8 соответствующих переменных гидравлических сопротивлений 13 и 10 делителя потока; Q М 1 и Q М 2 — полные расходы рабочей жидкости через гидравлические моторы М1 и М2;

Таким образом, предлагаемая модель системы синхронного гидромеханического привода щётки аэродромной уборочной машины позволяет производить расчёт системы привода щётки на установившихся и неустановившихся режимах работы с учётом взаимного влияния различных элементов системы (источника энергии, силового гидравлического привода и механической си- стемы) друг на друга и осуществить подбор и оптимизацию конструктивных параметров элементов системы.

Заключение. При проведении, как теоретических, так и экспериментальных исследований гидромеханической системы привода щётки, особое внимание следует уделить качеству работы подсистемы синхронизации — дроссельного делителя потока незолотникового типа с плунжерным задатчиком. Последнее требование связано с тем, что в рассматриваемом делителе потока, отсутствует герметичное разделение камер управления от соответствующих им вспомогательных камер, что может вызвать соответствующие негативные последствия. Предлагаемая в настоящей работе математическая модель позволяет выявить такие последствия и выработать пути борьбы с ними.