Синтез алгоритма нелинейной параметрической идентификации на основе критерия минимума вероятности ошибки оценивания

ВВЕДЕНИЕ                ПОСТАНОВКА ЗАДАЧИ ПАРАМЕТРИЧЕСКОЙ

ИДЕНТИФИКАЦИИ

Существующие методы решения задачи стохастической параметрической идентификации требуют, как правило, для своей удовлетворительной реализации принятия целого ряда крайне упрощающих ограничений (нормального вида распределения аддитивных помех наблюдаемых сигналов, линейности модели измерителя относительно параметров и т. д.). Это в большинстве реальных ситуаций оказывает значительное отрицательное влияние на качественные характеристики процедуры идентификации и, как следствие, снижает потенциально возможную точность получаемых оценок параметров [1-4].

В связи с вышеизложенным проведение исследований, направленных на синтез методов и алгоритмов, позволяющих в значительной (или полной) мере устранить недостатки традиционных методов, представляется весьма актуальным как с практической, так и с теоретической точек зрения.

Для решения данной задачи ниже рассмотрим подход, позволяющий, во-первых, избавиться от существующих ограничений разработанных методов, а во-вторых, повысить потенциальную точность процедуры идентификации за счет использования обобщенных вероятностных критериев, зависящих в общем случае нелинейно от апостериорной плотности распределения вектора состояния.

Для упрощения изложения синтеза процедуры идентификации и его наглядности остановимся подробнее на скалярном случае уравнений, определяющих в общем случае нелинейную модель исследуемого объекта и структуру его наблюдателя (обобщение на векторный случай, как это будет очевидно из последующих построений, особенностей не имеет).

Пусть дискретный объект задан в самом общем случае нелинейным разностным уравнением xk = f(xk-1, n)> (1)

где n — шум объекта с известной плотностью распределения вероятности q ( n ); x k — переменная состояния в к- й момент времени; f — известная нелинейная функция, допускающая обращение.

Наблюдение переменных состояния в дискретном времени осуществляется измерителем, описываемым в общем случае также нелинейным уравнением (уравнением наблюдения) следующего вида:

z k = X ⁽ c k , x k , w ), ⁽²⁾

где c _k — неизвестный искомый параметр наблюдателя, в общем случае нестационарный; w — шум наблюдения с известной плотностью вероятности g ( w ); x — известная нелинейная функция наблюдения; z _k — дискретный отсчет сигнала наблюдения. Для сокращения дальнейшей записи набор дискретных отсчетов сигнала наблюдения z_t ( i = 1,..., k ) обозначим через z k .

В рассматриваемом общем нелинейном стохастическом случае задача идентификации неизвестного параметра c _k может быть сформулирована как задача нахождения его значения, удовлетворяющего некоторому вероятностному критерию оптимальности J .

Исходя из физического смысла поставленной задачи идентификации, в качестве критерия J ис- пользуем далее критерий минимума апостериорной плотности вероятности (АПВ) текущей ошибки оценивания оk переменных состояния объекта на выбранном интервале ее предельно допустимого изменения — от оmin до оmax, т. е.

-to x J p(xk-11 z1k-1; ck-1) • p(xk I xk-1)dxk-1 • p(zk I xkX

-to

-to -to

h ⁽ c k ) = J J p ^{( x} k -11 ^z 1 ^{k -1} ; c k -1 ) ^x

-to -to

min J = min c_kc_k

^о max

J о min

р ^{( о} k I ^z 1 ^{k )d о} к ,

^x p ^{( x} k I ^x k -1 ^{)d x} k -1 • p ⁽ z k I ^x k ^{)d x} k ,

где о _k = x _k - x _k — текущая ошибка оценивания; x _k — текущая оценка переменной состояния объекта; р ( о _k I z k ) — апостериорная плотность вероятности ошибки оценивания.

Учитывая линейную зависимость значений ошибки о _k и переменной состояния x _k ( о _k = = x _k - 5с_к ), выразим АПВ ошибки оценивания р ( о _к I z k ) через АПВ переменной состояния p ( x _k | z k ; c _k ) (выражение для которой будет получено ниже):

р ^{( о} k I z ^k ) = p^{( о} k ^{- x} k I z ; c k ).

В этом случае минимизацию критерия идентификации можно представить следующим образом:

где

p ( x _k -1 1 z 1k ^-1 ; c _k -1 ) — определенная на ( k - 1)-м шаге АПВ параметра состояния объекта;

p ( x _k | x _k -1 ) — определяемая на текущем шаге алгоритма условная плотность вероятности переменной x _k ;

p ( z_k I x _k ) — определяемая на текущем шаге алгоритма функция правдоподобия.

Условную плотность p ( x _k | x _k -1 ) определим из исходного уравнения объекта при известном виде плотности распределения вероятности значений шума q ( n ) (в предположении их взаимной статистической независимости) [6]:

p ^{( x} k I ^x k -1 ) = q ⁽ Y ^{( x} k , ^x k -1 )) •

^d Y ^{( x} k , ^x k -1 ) ^{d x} k

о max min J = min [ ckck о min

р ^{( о} k I ^z 1 ^{k )d о} k =

^о max

= mm J p ^{( о} k ^{- x} k I z ^k ; c k ^{)d о} k .           (3)

ck о min

где y ( x _k , x _k -1 ) — полученная в результате обратного преобразования f ( x _k -1 , n ) однозначно определенная функция.

Аналогичным образом из уравнения наблюдения можно определить входящую в (4) функцию правдоподобия:

В результате проделанных построений поставленная задача сводится к отысканию плотности p ( о _k + x _k I z 1^k ; c _k ) и последующему определению значения искомого параметра из условия минимума критериального выражения (3).

p ⁽ z k I ^x k ) = g ⁽ W ⁽ z k , c k , ^x k )) •

a у ⁽ z k , c k , ^x k ) ^d z k

СИНТЕЗ АЛГОРИТМА НЕЛИНЕЙНОЙ ПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ

Для определения АПВ p ( о _k + x _k I z 1^k ; c _k ) предварительно используем выражение для АПВ p ( x _k | z 1k ; c _k ) с последующей соответствующей заменой переменных.

Известно [5], что апостериорная плотность вероятности информационного параметра x для k -го момента времени p ( x _k | z 1 ^k ; c _k ) определяется выражением

где у ( z _k , c _k , x _k ) — полученная путем обратного преобразования х ( c , x _k , w ) однозначно определенная функция.

Так как АПВ p ( x _k -1 | z 1 ^{k -1} ; c _k -1 ) в правой части равенства (4) является известной функцией (определенной на предыдущем шаге), рекуррентный алгоритм определения АПВ переменной состояния для k- го момента времени при наличии дискретных отсчетов сигнала наблюдения z ₁ ^k принимает вид

p ^{( x} k I z^k ; c k ) ^^k ’ ck ) ,           ⁽⁵⁾

h ⁽ c k )

где

p ^{( x} k I ^zk ; c k ) =

1 h ⁽ c k )

-to

^{л ( x} k , c k ) = J p ^{( x} k -1 1 ^z 1 ^{k -1} ; c k -1 ) • q ⁽ Y ^{( x} k , ^x k -1 )) ^x

-to d Y (xk, xk-1) dxk

d x k -i

• g ⁽ W ⁽ z k , c k , xk )) •

a у ⁽ z k , c k , xk ) ^d z k

+to h *( ck) = J л( xk, ck)d xk .

-to

Производя соответствующую замену переменных в (5) и обозначив критериальное выражение через Q ( c _k ), поиск минимума критерия (3) можно представить в следующем компактном виде:

min J = min Q ( c _k ),              (6)

ckck где

^( Ck ) = amax < k. к xA     aгГл^+xk,ck))

= I p^{( a} k ⁺ x k I z i ; c k ^{)d a} k = I —kr— — I d о k •

■„                                о v h ⁽ c k ) )

Здесь важно отметить, что в общем случае решения поставленной задачи оценка переменной состояния x ˆ _k , входящая в (6), представляет собой некоторый функционал (оператор) L от апостериорной плотности распределения переменной состояния, т. е. X _k = L ( p ( x _k | z k ; c _k ) ) , и, следовательно, в силу выражения (4), является нелинейной функцией от искомого параметра: X _k = U ( c _k ). .

Тогда критериальное выражение в (6) окончательно можно представить в следующем обобщенном виде:

σ max

^ ( C k ) = J

σ min

^{< л ( а} k ⁺ U ( c ) , c k ) v        h *⁽ c k )        >

d σ _k .

Идентификация параметра, удовлетворяющего выбранному критерию, предполагает минимизацию функции (7). Для этой цели в зависимости от конкретного вида получаемой функции Q ( c _k ) можно использовать известные и широко применяемые методы оптимизации: градиентный, метод Ньютона, метод сопряженных направлений, различные прямые методы и пр., выбор которых определяется особенностями исследуемого объекта и его наблюдателя.

ПРИМЕР

Для иллюстрации эффективности использования предложенного подхода рассмотрим следующий пример. Стохастический дискретный объект задан разностным уравнением xk = xk-i + n, xi = 3, где n — белый гауссовский шум с нулевым средним и дисперсией Dn = 0.01.

Наблюдение переменных состояния в дискретном времени осуществляется измерителем, описываемым уравнением zk = c • xk + w, где c — неизвестный искомый параметр наблюдателя (для рассматриваемого далее модельного примера выберем исходное значение искомого параметра c = 2 для всех k); w — белый гауссовский шум с нулевым средним и дисперсией Dw = 0.35.

Соответственно уравнение функции Q ( c ) для k -го шага алгоритма примет вид

σ max

П ( c ) = J

σ min

+to

J p ⁽ x k -11 ^z 1 ^{k -1 )} •

( a k ^{+ U ( c )-} x k -1 ) 2

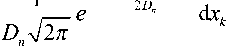
( z k ^{- c} •( ^a k ⁺ U ^{( c} )) ) ² ^ e 2D w D w -па

h ^* ( c )

v

+to +to                                ,            ( ^a k ^{+ U ( c )-} x k -1 ) ²

h *( c) = Г J p (Xk-1 |Z1k-1) • —^= e     2 Dnd

-to-to                 Dn

d σ _k ,

( z k ^{- c} •( ^a k ^{+ U ( c} )) ) ²

¹ e ^{2 Dw} d x . D 2 π ^k

Априорную плотность вероятности для первой итерации алгоритма ( k = 2) выберем нормальной с дисперсией D 0 = 1.5 и математическим ожиданием 2.5. При этом интересно отметить, что отклонения среднего значения априорной плотности от начального значения переменной состояния не оказывают в дальнейшем существенного влияния на качество процедуры идентификации (алгоритм идентификации к ним устойчив).

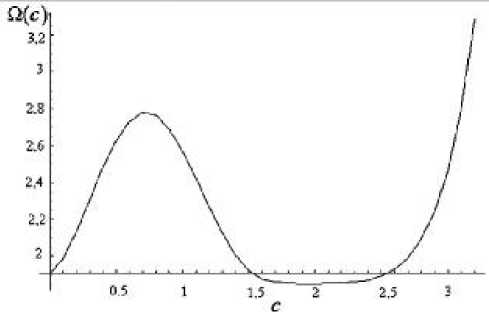
Зависимость функции Q ( c ) от искомого параметра ( k = 200).

Q ( c ) — критериальное выражение; c — искомый параметр наблюдателя; k — порядковый номер итерации алгоритма

Для определения текущего значения оценки переменной состояния объекта был использован оптимальный фильтр Калмана [5], который в рассматриваемом случае имеет вид хk = U(c)=хk-i + Kk •(zk -c• xk-i), x = 2-5;

K k = c •     , R_k =

Dw

+ , ( R k - 1 + D n   D w J

R 1 = 1.5.

Определение оценки искомого параметра c на очередном шаге алгоритма осуществлялось исходя из условия, определяемого выбранным критерием J , и предварительного задания границ допустимого интервала изменения текущей ошибки наблюдения ( о min = - 1.5 , о max = 1.5), а также замены бесконечных пределов интегрирования по переменной состояния x на конечные значения, удовлетворяющие точностным требованиям к алгоритму оценки ⁽ X mn = 0 , ^x max = 5).

На рисунке представлена полученная в результате моделирования зависимость критериального выражения Q ( c ) от искомого параметра наблюдателя на k -м шаге алгоритма ( k = 200).

Интегралы, входящие в выражения (8), определялись численно с использованием квадратурных формул с шагом А о = А х = 0.02.

Как показали результаты моделирования, вид приведенной на рисунке зависимости является характерным для критериальных выражений, получаемых на различных итерациях алгоритма (7). Здесь важно отметить, что, являясь многоэкстремальными, критериальные выражения на различ- ных шагах алгоритма (см. приведенный график) принимают свои наименьшие значения в районе истинного значения искомого параметра c = 2.

Для минимизации выбранного критерия на очередном шаге алгоритма, т. е. для однозначного определения численного значения текущей оценки искомого параметра, целесообразно, задав некоторый интервал возможных значений параметра c (в примере был выбран интервал 0 <  c <  8), воспользоваться одним из методов прямой минимизации. В данном случае использовался модифицированный симплексный метод прямой минимизации Нелдера—Мида, метод Бокса, обладающий достаточной вычислительной эффективностью и удобной программной реализацией [7].

Результаты компьютерного моделирования процедуры нелинейной параметрической идентификации показали, что при выборе количества дискретных значений сигнала наблюдения k ≥ 300 отклонение оценки параметра наблюдателя c от его истинного значения c = 2 не превышает 10 % от его величины.

Таким образом, результаты проведенных исследований подтверждают принципиальную возможность эффективной реализации метода нелинейной параметрической идентификации с использованием критерия минимума АПВ текущей ошибки оценивания.

ЗАКЛЮЧЕНИЕ

Полученное выше выражение (7) определяет общий вид алгоритма нелинейной параметрической идентификации, обладающего рядом принципиально новых свойств.

К их числу следует отнести:

• –    более высокий по сравнению с традиционными методами уровень потенциальной точности процесса идентификации за счет использования обобщенного вероятностного критерия, зависящего в общем случае нелинейно от апостериорной плотности распределения вектора состояния;

• -    инвариантность к виду плотности распределения вероятности шума как объекта, так и наблюдателя;

• -    возможность применения метода для нелинейных объектов и наблюдателей, в том числе при нелинейной зависимости функции наблюдения от параметра.

Таким образом, предложенный метод нелинейной параметрической идентификации на основе обобщенного вероятностного критерия может быть весьма эффективно использован в самых различных областях связи, управления, метрологии и т. д.