Синтез алгоритма определения координаты точки центра вымени и вершин сосков коровы в роботизированной доильной установке

Введение. В доильных роботах применяют различные технологии компьютерного зрения для обнаружения и локализации сосков [1–5]. Один из подходов включает использование RGBD-камер в сочетании с алгоритмами сегментации изображений и оценки положения сосков [6, 7]. Другая технология машинного зрения использует сверточные нейронные сети для распознавания сосков на основе непрерывного съёма изображений коров перед доильными станциями, достигая точности до 86% (патент на изобретение US 11,246,282 B2). Другие исследователи предлагают новый метод на базе модели YOLOv3 и LiDAR для обнаружения сосков в реальном времени в сложных условиях, при этом достигается скорость обнаружения до 0,415 секунды с повторяемостью до 94,9%, что подходит для практического применения на фермах [8]. Компьютерное зрение играет ключевую роль в увеличении эффективности и точности обнаружения и локализации сосков в автоматизированных системах доения [9]. Выходными данными в современных технологиях машинного зрения доильных установок является большой набор точек, полученный с использованием лазерного 3D-сканирования или других технологий, которые позволяют создавать 3D-представления существующей сцены [10].

Количественные и качественные показатели обнаружения координат вершин сосков в роботах для доения связаны с проблемами из-за сложных условий на молочных фермах, включая изменения освещения, наличие тени, формы и цвета сосков, а также локального загрязнения системы машинного зрения [8]. Негативное влияние данных условий приводит к потере информации и появлению артефактов, которые, как и шум, приводят к искажению облака точек, описывающего сцену, что приводит к ошибкам детектирования вершин сосков и их локализации [7, 11].

Как правило, алгоритм детектирования сосков можно разделить на несколько этапов, а именно:

• 1)    сегментация облака точек, описывающего вымя животного (патент на изобретение RU 2795709 C1);

• 2)    определение координаты точки центра вымени коровы, которая играет важную роль в обнаружении сосков, помогая точно локализовать соски на сцене;

• 3)    сегментация облака точек, описывающего соски животного, на которых не стоит запрет доения;

• 4)    определение координаты точки вершины сосков.

Сегментация облака точек на этапах 1 и 3 производится методом роста регионов, основанным на идее объединения точек в однородные области, удовлетворяющие заданным критериям (свидетельство о государственной регистрации программы для ЭВМ № 2021661988). Для текущей задачи существуют основные два критерия: во-первых, как региону разрешено расти между итерациями (т.е. какие соседние точки следует оценивать), и, во-вторых, само определение критериев роста. Простая реализация алгоритма роста двумерного региона за- ключается в том, чтобы на каждой итерации оценивать расстояние до 4 или 8 соседних точек текущего региона и сравнивать его с допустимым Ьд. Однако необходимо принять во внимание следующее:

• 1)    сцены, полученные под углом, содержат больше точек на передней стороне соска, чем на задней (если они вообще есть);

• 2)    присутствие искажений глубины по краям и разрывам;

• 3)    сегментация всегда начинается с кончика соска и растет вдоль соска, а в случае сегментации изображения вымени рост регионов продолжает расти и дальше.

Рисунок 1 иллюстрирует процедуру роста региона.

Итерация п

Итерация п+1

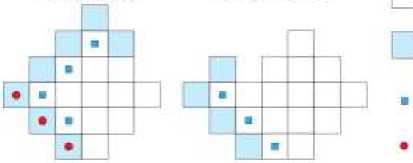
Облако точек на текущей итерации

Point cloud at the current iteration

Соседние точки текущего облака

Adjacent points of the current cloud

Точки, добавленные в облако точек на текущей итерации

Points added to the point cloud at the current iteration

Точки, соответствующие критерию роста региона

Points corresponding to the growth criterion of the region

Рисунок 1 – Иллюстрация процедуры роста двумерного региона Figure 1 – Illustration of the procedure for growing a two-dimensional region

На рисунке 2 представлен пример сегментации облака точек, описывающего вымя животного.

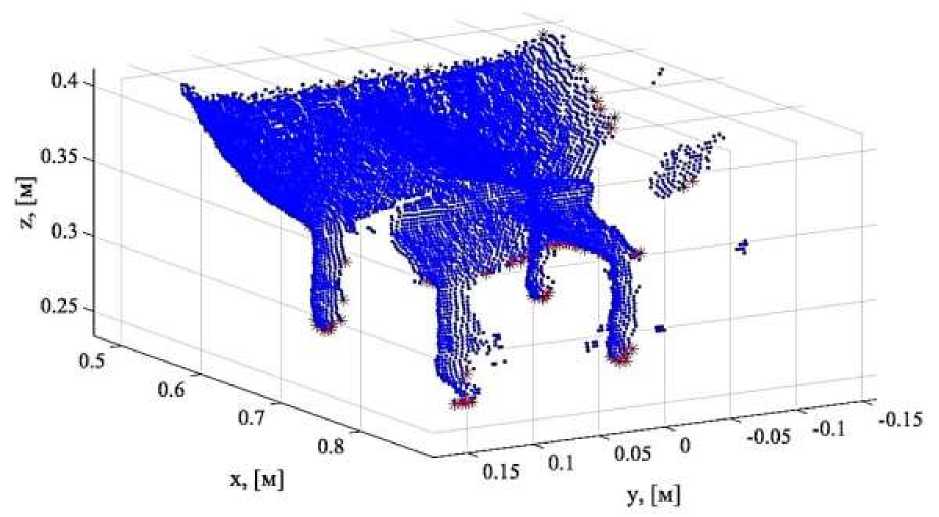
• – точка сегментированного облака точек; ∗ – точка, относящаяся к контуру сегментированного облака точек Рисунок 2 – Сегментированное облако точек вымени животного

• – point of segmented point cloud; ∗ – point related to the contour of a segmented point cloud Figure 2 – Segmented point cloud of a cow’s udder

Также возможно наличие других специфических критериев, которые будут зависеть от технических параметров самой системы машинного зрения, таких как, например, разрешение камеры. Потеря данных при реализации этапов 1 и 3 алгоритма детектирования нивелируется путем увеличения допустимого расстояния Ь д , что в свою очередь, не сказывается на качестве сегментации вымени или соска животного ввиду отсутствия посторонних предметов в зоне интереса. Этапы 2 и 4 алгоритма детектирования требуют дополнительных исследований и формирования критериев работы при условии влияния негативных факторов, которые приводят к потере информации.

Материалы и методы исследования. В рамках работы был проведен синтез алгоритма определение координаты точки центра вымени и вершины соска коровы. Проверка алгоритма производилась на 75 снимках, сделанных на времяпролетную камеру фирмы IFM. Камера размещалась в точке сканирования под коровой так, чтобы ее апертурные углы обхватывали периметр вымени и сосков коровы. На всех снимках во время испытаний искусственно имитировались сложные условия для проверки способности синтезированных алгоритмов нивелировать их негативные воздействия.

Синтез алгоритма определения координаты точки центра вымени на базе полиномиальной интерполяции. Процесс роботизированного доения в доильной установке начинается с захода животного в доильный бокс. После успешной идентификации животного вход- ные ворота в доильный бокс закрываются и рабочий орган манипулятора, на котором размещена система машинного зрения и доильные стаканы, позиционируется в точке сканирования. Далее производится снимок облака точек на времяпролетную камеру. Определение координаты точки центра вымени производится после сегментации облака точек, иллюстрированный результат которой представлен на рисунке 2. Автоматизированный алгоритм в машинном зрении почти всегда основывается на анализе данных, полученных на предыдущем шаге. В связи с этим необходимо выбрать такие данные (опорные точки, критерии) анализ синтезированным алгоритмом которых, даже при наличии сложных условий на ферме (потери информации), нивелирует их воздействие. Сложные условия на ферме могут привести к частичной потере точек на сосках коровы, при этом присутствие хотя бы малого их количества позволит определить нижний контур вымени с сосками в плоскости 0xz (при этом полное исчезновение таких точек не позволит детектировать координаты центра вымени из-за отсутствия каких-либо критериев и опорных ориентиров для их определения, кроме периметра самого вымени). Нижний контур сегментированного облака точек вымени представлен на рисунке 2 красным цветом. Если х1,х2,...,хп и z1,z2,...,zn координаты точек А1,А2,...,Ап контура облака точек вымени, которые распространяются слева направо, тогда угол наклона ai каждой точки контура относительно оси 0х можно рассчитать следующим образом:

J(x _{i + 1} - Xf)²

(Ц

= arccos                            ,где i = 1,2, ...,п —

V(x _i +i -x _i )²+(z _i +i -z _i )²

Тогда Aa _f = a _i+1 — a _f является абсолютным отклонением угла между точками контура облака точек. Данная величина характеризует угол распространения контура в плоскости 0xz , отклонение которого от некоторой величины E r будет характеризовать отвисшие части вымени, которыми являются соски. Для анализа нижней части контура облака точек необходимо построить некоторую функцию f(x), такую, что эта функция в узловых точках х 1 ,х ₂ ,...,х _т принимает значения Аа 1 , Ла ₂ ,..., Аа _т , то есть f(x _k~ ) = Аа _к для всех индексов к от 1 до т .

f(x) = а ₀ + a 1 x + a ₂ x²+... +а _т-1 х^{т 1}

Этого критерия совершенно недостаточно, чтобы однозначно определить интерполяционную функцию f(x). Необходимо уточнить ее вид. Очень часто функцию f(x) ищут в виде полинома. Степень полинома выбирается в соответствии с количеством узловых точек. В нашем случае количество узловых точек будет равняться сумме раз, когда Лак > Еr. Если узловых точек m, то степень интерполяционного полинома равняется m — 1. Такой полином имеет вид и содержит m - 1 параметров а1,а2,...,ат-1, благодаря которым удается добиться того, чтобы интерполяционный поли- ном проходил через базовые точки (хк,Дак) (индекс к = 1,2,...,т). Получаем систему алгебраических уравнений:

■ 1	х 1	х 2
1	х 2	х 2
1	х 3	х2
11	х к	хк

у т-1-. ^х 1 х т- х ^{т 1}

v т-1 хк

Г а0 1   ГДа^

. ^а 1    = ^Да 2

^а т-1]    [^Да ^|

V является квадратной матрицей с ненулевым определителем, то есть обратимой матрицей. Таким образом, учитывая V и у , можно найти искомое /(х) , решив для его коэффициентов а в уравнении Vа = Да :

а = V^-1 △ а.

Поиск минимума интерполяционной функции приведет к определению координаты х_С центра вымени. Применение полиномиальной интерполяции для изображения в плоскости 0yz с последующим поиском минимума функции приведет к определению координаты у_С центра вымени. Ближайшая точка облака точек к прямой параллельной оси 0z , проходящей через точку (х_С,у_С) , будет являться искомой точкой.

Синтез алгоритма определения координаты вершины соска на базе сингулярных разложений. Для точного детектирования координат вершины соска требуется синтезировать алгоритм детектирования, который будет устойчив к негативным условиям съемки изображения на молочной ферме. Для этого необходимо произвести поиск математического описания соска, которое включает кончик соска, ширину и его ориентацию. Аппроксимация поверхностью второго порядка, такой как эллиптический параболоид обеспечивает такое аналитическое решение. Метод основан на поиске поверхности, которая наиболее точно представляет набор точек в облаке. Наиболее точно означает, что общее расстояние между сегментированными точками и приближенной поверхностью минимизировано. Для аппроксимации облака точек поверхностью второго порядка в последних ис- следованиях были предложены несколько инновационных методов. Один из подходов – это метод приближенной внутренней воксельной структуры (AIVS), который включает предварительную обработку облака точек, изотропное упрощение и гибкое упрощение с внутренним контролем расстояния между точками [13]. Другой метод – это RepSurf, который вводит представительные поверхности для явного отображения локальных структур в облаках точек, достигая значительных улучшений в задачах классификации, сегментации и обнаружения на различных эталонных наборах данных [14]. Также разработан новый неявный прогрессивно-итеративный аппроксимационный фреймворк, основанный на радиальных базисных функциях (RBF), который изящно реконструирует кривые и поверхности, избегая вычислительных узких мест при решении линейных систем и обеспечивая высокое качество результатов [15]. Все вышеуказанные методы демонстрируют высокую точность, но весьма затратны для оперативного пространства, что серьезно сказывается на быстродействии системы.

Для экономии оперативного пространства и достижения приемлемой точности результатов аппроксимация облака точек поверхностью второго порядка производилась при помощи сингулярного разложения (SVD, Singular Value Decomposition). Если облако точек сегментированного изображения соска представляет собой набор точек {(x i ,y,z i )} , то аппроксимирующую поверхность второго порядка можно описать матрицей A :

A =

/ ^x2 ( ^x 2 \ x2

У2 7 2 z1 Х1У1 x1z1 y1z1 x1 У1 У2 7 2 z2 Х2У2 x2z2 y2z2 x2 У2 У2 z 2 zn хпУп xnzn ynzn xn Уп z1

^z 2

z n

Из теории справедливо выражение для сингулярного разложения SVD :

А = U£W^T, где U и W - ортогональные матрицы;

£ - диагональная матрица сингулярных значений.

Столбцы матрицы WT представляют собой собственные векторы, соответствующие сингулярным значениям в £. Для извлечения аппроксимирующей поверхности необходимо найти минимальное сингулярное значение в Е и соответствующий ему вектор v в W:

v' = (a,b,c,d,e,f,g,h,i,j)

Тогда уравнение аппроксимирующей поверхности примет вид:

ax² + by² + cz² + dxy + exz + f'yz + gx + hy + iz + j = 0 .

Использование сингулярного разложения позволяет эффективно и точно аппроксимировать облако точек вершины соска поверхностью второго порядка, минимизируя среднеквадратичное отклонение и обеспечивая надежное представление данных. Результат аппроксимации эллиптическим параболоидом основания соска животного позволяет определить точные координаты вершины соска.

Результаты исследования и их обсуждение. Синтезированные алгоритмы были апробированы на 75 снимках, которые были сняты на времяпролетную камеру. Для чистоты эксперимента были предусмотрены этапы испытаний, когда входные данные были подвержены негативному влиянию сложных условий фермы (искусственному удалению точек из облака точек) для фиксации стойкости синтезированных алгоритмов к неблагоприятным условиям.

На рисунке 3 представлена иллюстрация применения полиномиальной интерполяции для поиска координаты точки центра вымени.

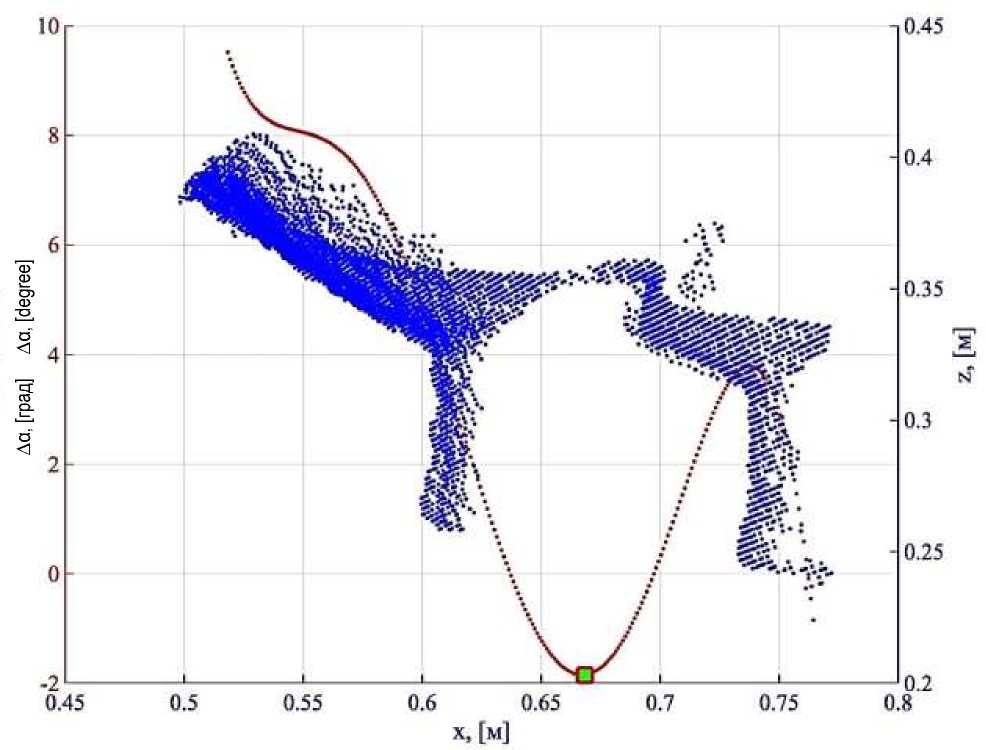
Рисунок 3 – Применение полиномиальной интерполяции для поиска координаты точки центра вымени Figure 3 – Application of polynomial interpolation to find the coordinates of the udder center point

Синтезированный алгоритм был сопо-   кости 0xy. В таблице 1 представлены результа- ставлен с работой алгоритма детектирования ты исследования.

на основе данных о периметре вымени в плос-

Таблица 1 – Результаты исследований методов детектирования координаты центра вымени Table 1 – Results of research methods for detecting the coordinates of the udder center

Процент негативного влияния на выборку из 75 снимков Percentage of negative impact on a sample of 75 images	Количество успешных экспериментов Number of successful experiments
	Алгоритм детектирования на основе данных о периметре вымени в плоскости 0xy Detection algorithm based on data on the perimeter of the udder in the plane 0xy	Алгоритм детектирования на основе последовательной полиномиальной интерполяции данных плоскости 0xz и 0yz Detection algorithm based on sequential polynomial interpolation of plane data 0xz and 0yz
0%	70	75
10%	68	75
20%	59	75
30%	33	75
40%	21	73
60%	3	55
80%	0	48

Успешным детектированием центра вымени во время эксперимента считалось определение такой точки, которая своим географическим расположением в пространстве разделяла облака точек всех сосков по четвертям, образующихся путем пересечения двух плоскостей, проходящих через найденную точку, которые в свою очередь ортогональны плоскостям 0xz и 0yz . Точность и качество расположения самих облаков точек каждого соска в соответствующей четверти в рамках данного эксперимента не учитывались.

Результаты эксперимента наглядно показывают негативное влияние сложных условий на молочной ферме на стандартную работу алгоритма детектирования на основе данных о периметре вымени в плоскости 0xy. Даже при идеальных условиях алгоритм детектирования по периметру демонстрирует свою работоспособность только в 93,3% от общего количества экспериментов, при этом алгоритм на базе полиномиальной интерполяции устойчив в 97,3% случаев даже при условии наличия негативного влияния, приведшего к потере до 40% изображения.

Синтезированный алгоритм детектирования координат вершины соска на базе сингулярного разложения был сопоставлен с работой алгоритма детектирования на основе полиномиальной интерполяции. Иллюстрация работы алгоритмов представлена на рисунках 4 и 5 соответственно.

В таблице 2 представлены результаты исследования.

Эксперимент проводился при условии ручных фиксаций центральной точки вымени и сегментации облаков точек для каждого соска независимо от качества входных данных, для устранения каких-либо негативных влияний на работу исследуемых алгоритмов. В рамках данного исследования эксперимент являлся успешным, если абсолютная точность детектирования вершины соска в пространстве составляла не более 3,5 мм.

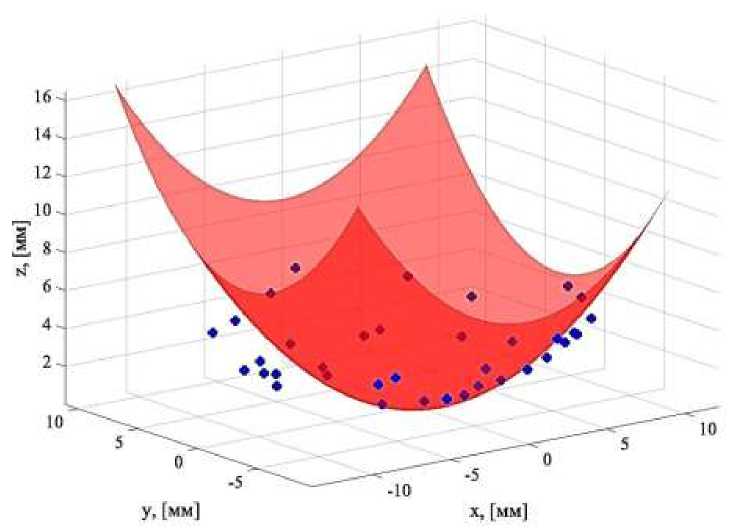
Рисунок 4 – Аппроксимация вершины соска поверхностью второго порядка Figure 4 – Approximation of the top of the nipple with a second-order surface

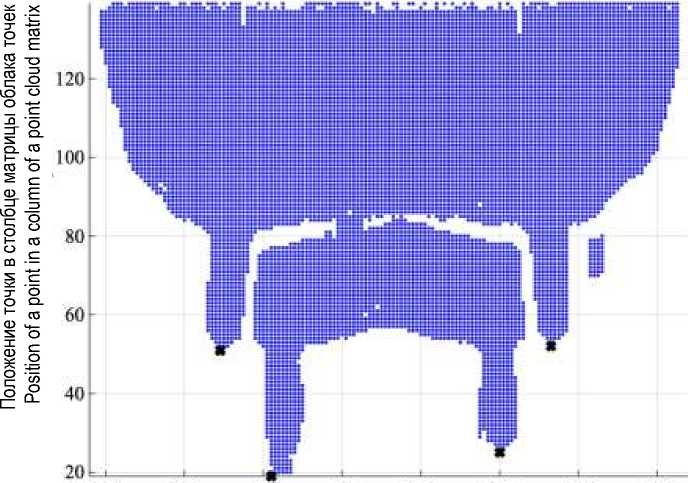
100     120     140     160     180     200     220     240

Положение точки в строке матрицы облака точек Position of a point in a row of the point cloud matrix

Рисунок 5 – Применение полиномиальной интерполяции для поиска координат вершин сосков Figure 5 – Using polynomial interpolation to find the top of the nipple

Таблица 2 – Результаты исследований методов детектирования вершины сосков Table 2 – Results of research methods for detecting the top of the nipples

Процент негативного влияния на выборку из 75 снимков Percentage of negative impact on a sample of 75 images	Количество успешных экспериментов Number of successful experiments
	Алгоритм детектирования вершин сосков на базе полиномиальной интерполяции Detection algorithm for the top of the nipples based on polynomial interpolation				Алгоритм детектирования вершин сосков на базе сингулярных разложений Detection algorithm for the top of the nipples based on singular value decompositions
	передний левый anterior left nipple	задний левый rear left nipple	задний правый rear right nipple	передний правый anterior right nipple	передний левый anterior left nipple	задний левый rear left nipple	задний правый rear right nipple	передний правый anterior right nipple
0%	72	74	73	74	75	75	75	75
10%	68	64	64	65	75	75	75	75
20%	53	55	55	54	75	75	75	75
30%	42	39	78	41	75	75	75	75
40%	9	15	13	8	73	75	74	75
60%	3	3	0	1	67	69	68	71
80%	0	0	0	0	42	46	33	38