Синтез алгоритмов управления рабочим столом 5D принтера с параллельной кинематикой

Механизмы с параллельной кинематикой за последнее время получили достаточно большое распространение [1,2], особенно в механизмах, требующих значительных скоростей движения рабочих органов и большое быстродействие.Число степеней свободы подвижного рабочего органа выбирается исходя из требований, предъявляемых к механизму, в нашем случае -5 степеней: координаты X, Y, Z, A, B).Отличительной особенностью механизмов с параллельной кинематикой заключается в том, что управляемые координаты приводов зависимы, поэтому, поэтому положение точки на рабочем органа при движении по одной из декартовых координат зависит от всех управляемых координат приводов.

На рисунке 1 приведена схема механизма с параллельной кинематикой. Подвижный рабочий стол предназначен для размещения на нем в центральной точке специального сопла «печатающей» головки с нагревателем, через который подаётся расплав неорганического вещества. Управляя положением сопла, с определённой ориентацией положения кромки сопла, на которой находится микро капля расплава, по трём декартовым координатам, с добавочными наклонами сопла по координатам А и В (повороты вокруг оси Х и У ), можно «напечатать» трёхмерный каркас со сложной поверхностью и порами, имеющие сложную пространственную ориентацию. Число требуемых управляемых координат, для обеспечений пространственной ориентации рабочей точки, зависит, как от ориентации координат привода и их вида ( линейные или угловые перемещения), так и числа степеней подвижности, обеспечиваемыми шарнирными опорами ( 2 или 3 степени).

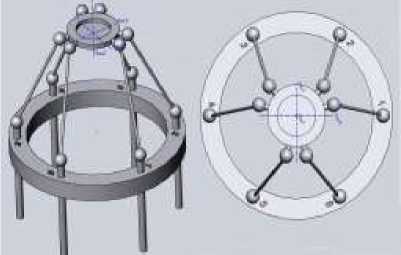
Рис.1. Кинематическая схема 5D-принтера..

(цифрами на неподвижном основании обозначены номера координат приводов – направление их движения ориентированы по оси Z )

В выбранной схеме все шаровые опоры имеют три степени свободы, все приводы обеспечивают линейное перемещение толкателей вдоль оси Z и расположены на образующей цилиндра с постоянным радиусом. Толкатели попарно сгруппированы, а пары,в угловом отношении, расположении под углом 120°. Аналогично попарно сгруппированы опоры на подвижном, столе.Шатуны с шаровыми опорами имеют одинаковую длину.

Анализ кинематики по виртуальной модели показал, что при определённом расположении толкателей с опорами в диаметральном сечении опор на рабочем столе, пространственное положение шатунов, обеспечивают устойчивое положение сопла во всем рабочем объёме и, одновременно, и образуется большое количество секторов в цилиндрической системе координат, обладающих свойствами симметрии.

В большинстве работ, посвящённых анализу механизмов с параллельной кинематикой,решается прямая задача:задано движение рабочей точки и по аналитическим зависимостям требуется установить связь этих координат с координатами управляемых приводов в цилиндрической системе:

M ( r , ф, z , A, B ) = P ( pl, p 2, p 3, p 4, p 5, p 6) (1)

Где векторы с координатами рабочей точки и, соответственно, каждого из приводов.

На основании этой системы уравнений разрабатывается алгоритм для настройки контроллера[2] и вносятся элементы коррекции для индивидуальной настройки механизма при отклонении размеров звеньев, и их расположений. Это также усложняет программу для контроллера.

Для существенного сокращения вычислений в контроллере, необходимо каждое заданное положение вектора и вектора , априори, измерить с требуемой точностью и записать их в два взаимосвязанных, многомерных массива: массив c компонентами ( x, y, z,a,e ) и массив P (p 1 ,p₂,p₃,p₄,p₅,p₆ ). Тогда алгоритм управления сводится к простому поиску в массиве P, связанном с массивом M посредством указателя, требуемых компонент p_t (I =i...6) . Координата z, может быть опушена в связи с ориентацией осей приводов по оси Z , поэтому новое требуемое значение z потребует изменения координат p i , (i = 1...6) на такую же величину.

Рассмотрим подробно, каков объем данных требуется для хранения всех точек рабочей области, если границы этой области определены вектором: -( г_о,ф_о,а_о.в 0 ,О ). Если задана точность позиционирования печатающей головка в точке M j , то, в качестве примера, рассмотрим следующие габариты рабочего пространства: -( r₀ : =25мм,ф₀:=360°,а₀:=20°, в₀:=20° ), а требуемую точность определим как - ( Дг=0.02мм, Лф=0.005°, 4а=0.01°, Лв=0.01° ) После расчёта получаем требуемое количество точек по каждой из координат в заданном рабочем пространстве - ( r:=12500, ф: = 72000, а:= 2000, в^:= 2000 ). Практическая реализация этого алгоритма потребует огромный объем памяти.

Расположение толкателей привода на основании и опор шатунов на столе выбрано так, что измерения в одном (1)симметричном секторе по координатам ф(1)rсоответствуют другому сектору (2) с разницей смещения угла φ(2). При этом меняется лишь последовательность нумерации или чередование номеров приводов в массиве P. Исследования показали, что по координате ф можно ограничиться измерениями в секторе в 30°,а с учётом чередований - в секторе в 15°. Это позволяет сократить объем памяти более чем на порядок, однако она ещё достаточно велика.

Дальнейшая редукция данных связана с известной системой G– кодов: для траектории задаются опорные точки, а промежуточные точки вычисляются простой линейной интерпретации.Исследования виртуального 5D – модели позволили определять координаты опорных точек вектора M , обеспечивающих необходимую точность,со следующими значения интервалов: -( дг₀ =0.2мм, дф₀=0.1°, 5а₀=0.5°, бр₀=0.5° ). Количество опорных точек в массиве M резко сокращается и равно - (r=125, ф= 300, а= 40, в= 40 ).В результате общее количество точек, требуемых для описания рабочего пространства вектора и вектора ,сократилось на 4 порядка.Заметим, что расстояния между двумя опорными точками выбирались исходя из требуемой точности определения промежуточных координат вектора .

CAD –системы позволяют, путём исследования движения сборки или путём управления сопряжениями в сборке, определить интересующие координаты и произвести их автоматическую запись в файл, и задача определения этих двух матриц решена.. Дальнейшая работа с полученными массивами, заключается в создании структурированных связанных списков с указателями [3].Алгоритм сводится к поиску по заданной точке вектора М новых компонент вектора Р в области двух смежных опорных точек без вычислительных процедур.Системе управления принтером и время «печатания» объекта сокращается.