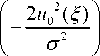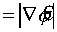Синтез бинарного фокусатора в произвольную кривую в электромагнитном приближении

• 1.1.    Геометрооптический расчет фокусаторов (общие сведения)

Пусть лазерное излучение с комплексной амплитудой Eo (х) = 10 (х) exp [ik(Sx)], где 10 (х) - интенсивность освещающего пучка, к = 2л/Л, X - длина волны освещающего пучка, х - набор декартовых координат в трехмерном пространстве, падает на отражательный оптический элемент с апертурой D, расположенный в плоскости й = (u, v), который преобразует падаю излучение в поле E(й) = ^10 (u) exp[ik^(w)].

Задача состоит в отыскании функции ф ( и) , которая должна обеспечивать в плоскости z=f с декартовыми координатами (x,y) формирование светового поля, сфокусированного вблизи каустической фокальной кривой. Считаем, что фокальная кривая (Рис.1) задается следующими параметрическими уравнениями *

x - X( 5 ), 5е [0, / ]                          (1)

Рис. 1. Фокусировка в произвольную фокальную кривую

В работах [1-2] приведен метод расчета фо-кусатора в кривую, основанный на геометрооптической аппроксимации оператора распространения комплексной амплитуды света. Распределение энергии вдоль фокальной кривой характеризуется линейной плотностью. Фокальная кривая представляет собой вырожденную каустику, поэтому большое значение имеют дифракционные эффекты, которые не учитываются при геометрооптическом подходе к решению обратной задачи фокусировки.

Для того чтобы охарактеризовать распределе -ние световой энергии вдоль каустической фокальной кривой, введем в окрестности геометрической кривой криволинейные координаты по формулам:

x ( 5 , , n , ) = X ( 5 , ) + Y ' ( 5 , ) n ,

У ( 5 , , n , ) = Y ( 5 1 ) - X ' ( 5 , ) n ,

Распределение энергии вдоль фокальной кривой будем характеризовать функцией 9 (^, s )

+ Е

9(5,, Е) = JI(51, n,)dn, , — Е где I - средняя плотность потока вектора Умова-Пойнтинга в плоскости фокусировки.

Пусть А - дифракционная ширина фокальной кривой.

При 2 е >> А функция 9 (^, s ) представляет собой линейную плотность энергии вдоль отрезка [,].

При 2 е << А функция 9 (^, s ) пропорциональна интенсивности светового поля на геометрической фокальной кривой.

Будем искать решение, при котором все геометрооптические лучи выходящие из “фокусирующей кривой”, расположенной в плоскости оптического элемента, попадают в одну точку на фокальной каустической кривой. Фокусирующую кривую согласно [,], будем называть слоем.

Уравнение слоя на фокусаторе имеет вид [,] [ ( u — X ( 5 ) ) X ' ( 5 ) ] ² = c ²( 5 ) [ f + ( и — X ( 5 ) ) ² ] , (2)

представляющий гиперболу, где c( 5 ) - константа, определяемая из энергетических соотношений.

Определяя из (2) соответствие 5 = 5(и) и под ставляя его в уравнение наклонов [3]

——

X ( 5 ( г—)) — г—

^ф =

,

[ f ² + ( X ( 5 ( й )) — г—) ) ² ] ²

можно найти 5 = 5 ( и ) , а затем восстановить ф ( и )

методами теории потенциала: г—

ф ( — - ф ( и ₀) + J V ^ d u ,                (4)

— где интегрирование ведется по произвольной кривой, соединяющей точку и с некоторой начальной точкой и0

v -f хд 1 .

( du д J

• 1.2.    Анализ эффективности бинарного фокусатора в произвольную кривую в электромагнитном приближении

В предыдущем пункте приведен метод расчета фокусаторов лазерного излучения в произвольную фокальную кривую. Были получены формулы для фазовой функции оптического элемента, осуществляющего данную фокусировку. Для того чтобы изготовить дифракционный оптический элемент (ДОЭ), необходимо знать функцию высоты микрорельефа. Расчет высоты микрорельефа ДОЭ по заданной фазовой функции рассмотрен в работах [,-2]. В этих работах расчет высоты микрорельефа по заданной фазовой функции оптического элемента был основан на приближении геометрической оптики. Следует отметить, что приближение геометрической оптики в данном случае справедливо, если ширина зоны на дифракционном оптическом элементе составляет несколько десятков длин волн. Однако для многих технических приложений актуально использование короткофокусных ДОЭ. Средняя ширина зоны на таком оптическом элементе приблизительно равна длине волны освещающего когерентного излучения.

В данной работе будут рассмотрены некоторые методы создания заданных фазовых распределений, основанные на представлении ДОЭ в виде набора дифракционных решеток с различным направлением штрихов и различным периодом.

Для того чтобы решить поставленную задачу, рассмотрим отражение плоской электромагнитной волны от идеально проводящей дифракционной решетки.

Пусть плоская волна exp( iksx) падает на дифракционную решетку, расположенную в плоскости, определяемой вектором нормали N . Штрихи дифракционой решетки направлены вдоль вектора ^f (рис 2).

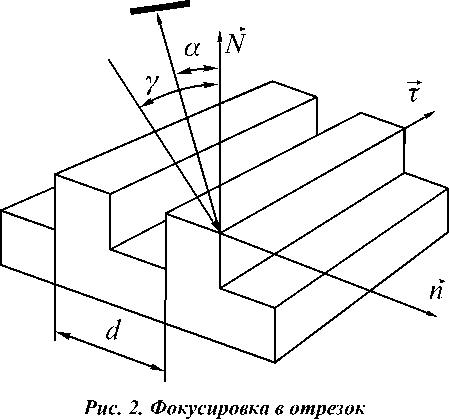
Отраженное поле представляет собой суперпозицию

W ^{( Х )} = Е R n exP⁽ ika n x                   ⁽⁵⁾

где a n - определяет направление отраженных волн. Согласно результатам, полученным в [4],

5 m = ( a ₀ ^f ) ^f + ( a ₀ 5 + A m / d ) n +

+7 (1 - ( a ₀ f )² - ( a ₀ n + A m / d )²) N

где a ₀ = ^f - 2 N |_ N * ^f J , n = [ ^f * N ] - вектор нормали к штрихам решетки, d - период решетки.

Проводя анализ формул (5) и (6) нетрудно заметить, что при отражении от решетки волна получает дополнительный сдвиг фазы

А ф т = ■⁽ "n ) ⁺ arg ^R m ⁽ u , V ) . ⁽⁷⁾ d ( u , v )

Это свойство дифракционных решеток придавать при отражении дополнительный сдвиг фазы в дальнейшем будем использовать для создания требуемых волновых фронтов.

Пусть требуется создать в плоскости z=0 фазовое распределение ф (u , v ), где u = ( u , v ) - декартовые координаты в плоскости оптического элемента.

Рассмотрим плоскую волну exp(iksx), падающую на плоский отражательный фазовый корректор, который рассматривается в дальнейшем как дифракционную решетка с переменным периодом и направлением штрихов. Фазовое распределение в падающей волне имеет вид

Ф ₀ ( u , v ) = k ( 50 ^f ) ^f u + k ( a ₀ 5 ) n5 .               (8)

После отражения фазовое распределение обретает вид

ф ( u , v ) = Ф 0 ( u , v ) + ^ф _m == k ( 5 0 ^f ) ^f 5 +

+ k\ ( a₀n ) n + ^m 5 ^5 + arg R ( u , v ) c ²     d ( u , V ) )      -        '

.

Предположим, что d(u,v) и R m (x,y) есть ленно меняющиеся функции, тогда

, ^Am . n = V ( ф ( u , v ) - C o 5) .

d ( u , v )

при-

мед-

Из формулы (10) видно, что границы штрихов решетки (или границы зон фазового корректора) совпадают с линиями уровня функции

ф (u , v ) = ф ( u , v ) - a ₀ 5 .

Следует отметить, что границы зон на ДОЭ, вычисленные по формуле (11), не совпадают c границами зон ДОЭ, микрорельеф которого находится в приближении геометрической оптики. Отличие от подхода, изложенного в работах [1,2,5], посвященных синтезу фокусаторов в скалярном геометрооптическом приближении, состоит в предположении, что локальные дифракционные решетки, из которых состоит ДОЭ, имеют только один дифракционный порядок. Действительно, если ширина зон на дифракционном оптическом элементе составляет несколько десятков длин волн, это предположение справедливо с достаточной степенью точности.

С другой стороны, в скалярном приближении бинарный ДОЭ всегда имеет низкую дифракционную эффективность (приблизительно 40%), и ее в данном приближении нельзя повысит никакими методами. Используя строгую электромагнитную теорию, можно рассчитать ДОЭ с высокой эффективностью, значение которой в некоторых случаях приближается к 100%. Это происходит потому, что в строгой электромагнитной теории (в отличие от скалярной теории) дифракционная эффективность в соответствующем дифракционном порядке сильно зависит от ориентации падающей волны по отношению к плоскости дифракционной решетки и периода дифракционной решетки. Выбирая эти параметры можно добиться высокой (приближающейся к 100%) дифракционной эффективности в заданном дифракционном порядке.

Методы расчета бинарных дифракционных решеток в электромагнитном приближении подробно рассмотрены в работе [4]. В данной работе мы ограничимся лишь изложением основных результатов.

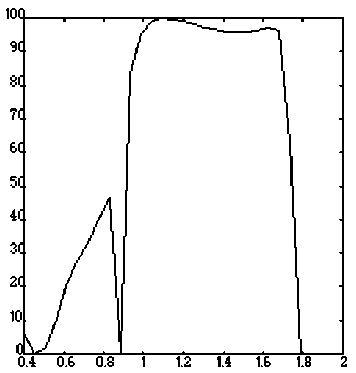
Из анализа результатов расчета, приведенных на рис. 3, видно, что в случае s-поляризации (вектор электрического поля перпендикулярен направлению штрихов дифракционной решетки) максимальная дифракционная эффективность в минус первом порядке дифракции достигается при отношении 0,8 < —0 dd < 1,8

— 0 =      ^—

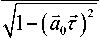
s , %

х /а

Рис. 3. Зависимость дифракционной эффективности отражательной дифракционной решетки от отношения X/ d

Для достижения максимальной дифракционной эффективности при синтезе ДОЭ необходимо, чтобы ширина зон на дифракционном оптическом элементе находилась в заданных пределах.

Пусть зависимость дифракционного коэффициента в соответствующем дифракционном порядке описывается функцией eff n = F n ( — ₀/ d ) .

Тогда локальная дифракционная эффективность представляется в виде eff (u, v) = F f 2uv) 1                   (13)

( d ( u , v ) )

A o ( x , y ) =       ^—                             (14)

V 1 - ( a , ? ) ²

й( u, v) = * v ф u, v, a j х n _(V(

Определим общую дифракционную эффективность дифракционного оптического элемента по формуле

£⁽«) =

ЦI₀ (u, v) eff (u, v) dudv

D

JJ1₀( u, v) dudv

D

где D - область оптического элемента, а I₀- интенсивность в плоскости ДОЭ.

Данная величина определяет долю энергии освещающего пучка в рабочем дифракционном порядке. Для создания высокоэффективного ДОЭ необходимо максимизировать данную функцию.

Преобразуем полученное выражение к более простому виду

е⁽«) =

JJ10( ? F

D

(Уф)²

m(Уф)² - а₀[Уфх N]²

dudv

------, (19)

JJ 1₀ (u) dudv

D

где V ф согласно уравнению наклонов имеет вид

-       X (5( й, a)) - г?       ^^?

V ф =-------------------------- - (a₀n)n - (a₀т)т (20)

[ f1 +(X(5(г?, a)) - и))²1²

где 5(й а) - функция соответствия точек на фокуса-торе и точек на фокальной кривой.

• 1.3.    Синтез фокусатора Гауссова пучка в отрезок

• 2.2  2

В качестве примера рассмотрим расчет бинарного фокусатора в отрезок (см. рис.2).

Пусть плоский Гауссов пучок падает на отражательный ДОЭ под углом у к нормали к поверхности дифракционного оптического элемента.

В этом случае модуль комплексной амплитуды падающего пучка в плоскости ДОЭ имеет вид

u + v cos у

E (u,v) = exp

где ст - параметр, характеризующий ширину падающего Гауссова пучка.

Параметрическое уравнение для отрезка имеет следующий вид x (5) = - L+5

Y (5) = f • tga

где L - длина фокального отрезка.

Уравнение слоя на фокусаторе принимает вид гиперболы

(u -5 + L/2)2 (v- f • tga)²= 1 a²(5)            b²(5)     "

^{a (5)}=

c (5) f

. 4 1 - c² (5))

= f 0(5

b (5 ) = f

Для решения поставленной задачи необходимо решить систему дифференциальных уравнений (3). Решение системы в Декартовых координатах доста- точно сложная математическая задача. Однако данная система имеет определенные свойства симметрии, и ее решение существенно упрощается при выборе соответствующей системы криволинейных координат.

Введем в плоскости фокусатора криволинейные координаты, связанные со слоями:

и (5, п ) = 5 — L/2 + в(5) • d (п) v (5, п ) = п

где d(п) = Vf²+ (п — ftga)² .

В плоскости фокусировки вблизи фокального отрезка введем координаты по формулам x (51, п^ = — L + 5

2                 -

У ⁵П1) = ftg«⁺П1

Уравнение наклонов (3) в данных криволинейных координатах приобретает простой вид

5ф = _ в(5)(1 + в'(5) d (п))

• 55          (1 + в2 (5))

Эф = (ftga — п) ^1 + в² (5) дп            d (п)

Интегрирование данной системы дифференциальных уравнений дает выражение для фазовой функции ДОЭ

ф(5, п) = -j ^(t)— dt - 41 + в²(5)d (п)       (26)

^JoV1 + в²( t)

Распределение энергии вдоль фокального отрезка будем характеризовать функцией

+ £

^5,^£) = J I5 п1)d^ ,

— £ где £ << А, А - дифракционная ширина отрезка, I(5, п1) - распределение интенсивности в фокальной плоскости.

В этом случае функция 9 пропорциональна интенсивности на геометрическом отрезке.

Для вычисления интенсивности электромагнитного поля на данном отрезке воспользуемся интегралом Кирхгофа-Гюйгенса [6], записанным в криволинейных координатах f ize fexp(ik (^(5, п) + R(x,5, п)))                f2

⁹⁽ x) = tJJ---------.---------^хJ^(5,п ) ^d5dn

^ V¹         R (x,5,п)                       ^

L x = — + 5

R (x,5 п) = Vf 2 + (x — u(5, п))2 + (f • tga — v(5, п))2 , где

J (5, п) = E (и (5, п), v (5, п)) J0 (5, п)          (27)

J₀(5, п) - Якобиан преобразования Декартовых координат и = (и,v) к криволинейным координатам (5, п) -

Для вычисления интеграла по переменной ^ воспользуемся методом стационарной фазы [7].

Уравнение на стационарную точку имеет вид дф(5, п) + д f2 +(x — и (5, п) )2 +(ftga — v (5, п) )2

Решение данного уравнения позволяет установить связь между координатами в фокальной плоскости и криволинейными координатами на фокуса-торе

5 = 51.

Проводя вычисление интеграла указанным ме- тодом, получаем выражение для интенсивности све- тового поля на отрезке

C9(—L + 5) =

___________________2

z I 2

^4 41 + в²(5)

да

J E (и (5, п), v (5, п)) х да

х ^{1 + в5}) ^{d (}п)dп

4   d ^Зп)

где C - коэффициент пропорциональности, определяемый из граничных условий.

Нетрудно заметить, что выражение (30) представляет собой обыкновенное дифференциальное уравнение относительно функции в(5). Решая данное уравнение и подставляя его решение в (26), получим окончательное выражение для фазовой функции оптического элемента и уравнение для слоев на ДОЭ.

В параксиальном приближении d (п) « d₀ = f /cos а и слои на оптическом элементе представляют собой прямые линии параллельные оси v.

В этом приближении для Гауссова пучка дифференциальное уравнение для функции в(5) приобретает простой вид

L N9(— - + 5) =

П ^га² 2d³₀ cos²у

х

_х1 + в'(5) d 0

V1 + в²(5)

и 0(5) = 5—-+в(5) d 0

где d₀= f / cos а .

Коэффициент пропорциональности находится из условия

—L /2 + в(— |) • d(0) > да .

^в(|) • d⁽⁰⁾>^+да

Из (31) видно, что полученное решение для функции в (Q (а значит и для искомой функции ср зависит от двух углов а и у. Для достижения максимальной дифракционной эффективности необходимо выбрать их значения из условия максимума функционала (19).

Используя предложенный метод расчета был синтезирован высокоэффективный бинарный фоку-сатор Гауссова пучка в отрезок со следующими параметрами: Х=10,6 мкм; L=2 мм; g=2 мм; I(^)=const, 0<^<L/2.

Оптимальные значения углов а и у имеют следующие значения: у=45°; а=25°.

При данных параметрах направление падающей волны перпендикулярно направлению штрихов на оптическом элементе, поэтому в формуле (19) можно положить

(V()²

m(^ (р)^ - a₀[V(tx N]²

И выражение для общей эффективности оптического элемента принимает вид jj10(u, v)Fm [(Vр(J dudv e = D----^---------------- .            (33)

jj 1₀(u, v)dudv

D

Кроме того, при данный параметрах оптической системы пространственная частота линий на ДОЭ изменяется достаточно слабо, поэтому мы вправе положить |V(p = const, и выражение для эффективности фокусатора в отрезок принимает простой вид e = Fm (const) .

При стремлении длины фокального отрезка к нулю результат, полученный в данной работе, совпадает с результатом, полученным в работе [8] для бинарной линзы.

Предложенный метод синтеза можно без ограничения общности распространить на синтез фоку-сатора в произвольную фокальную кривую с произвольным распределением энергии вдоль нее.

Данная работа выполнена в рамках Региональной научно-технической программы “Конверсия Самары” при финансовой поддержке Администрации Самарской области, Министерства науки и технической политики России и Самарского научнокоординационного центра “Перспектива”.