Синтез цепного поступательного привода обрабатывающих машин

Практика машиностроения показывает, что во многих случаях кинематические схемы могут быть значительно упрощены, если этому уделять особое внимание при проектировании.

В результате анализа взаимодействия подсистем обрабатывающих машин в рабочем процессе установлены требуемые базовые параметры технических характеристик передач для перемещения рабочего органа станка [1]:

• -    величина тягового усилия на уровне 65–80 кН;

• -    диапазон скоростей подач в пределах 1–5000 мм/мин;

• -    величина скорости ускоренного перемещения больше 10000 мм/мин;

• -    диапазон ускорений при разгоне 1,47–4,4 м/с²;

• -    частота собственных колебаний исполнительного механизма не менее 60 Гц;

• -    приведенный момент инерции вращающихся деталей механизма подач должен быть предельно минимальным.

Цель работы . Разработка схемы поступательного привода со значительными ходами перемещения рабочего органа.

При разработке схемы поступательного привода обрабатывающих машин были поставлены следующие задачи :

• п ровести теоретические исследования и разработать методику расчета кинематических параметров взаимодействия звена цепи с рабочим органом, совершающим возвратно-поступательное перемещение;

определить возможность плавного изменения динамических параметров в крайних положениях.

Для решения поставленных задач будем использовать теоретическую модель цепного привода, расчет и графический анализ с использованием известных положений теории машин и механизмов.

Известные поступательные приводы перемещения режущего инструмента имеют ограничения по скорости и ускорениям рабочего органа, связанными с мгновенными изменениями направления движения в крайних положениях.

Применение цепной передачи в поступательных приводах обрабатывающих станков позволяет наиболее просто осуществлять передачу вращения от двигателя к исполнительному механизму станка.

Цепные приводы имеют значительные тяговые усилия, допускаемый диапазон скоростей подач до 1 м/с, диапазон ускорений до 10 м/с2 и плавное изменение кинематических и динамических параметров в крайних положениях. Такие цепные приводы могут обладать необходимой гибкостью, бесшумностью, работой без вибрации и проскальзывания, амортизируют легкие точки и удары [2].

На рисунке 1 изображена схема реализации работы цепного привода, вращающего звездочки радиусом r, и натянутой на них цепью, на поводке которой подвижно закреплен режущий инструмент или любой производящий полезную работу орган.

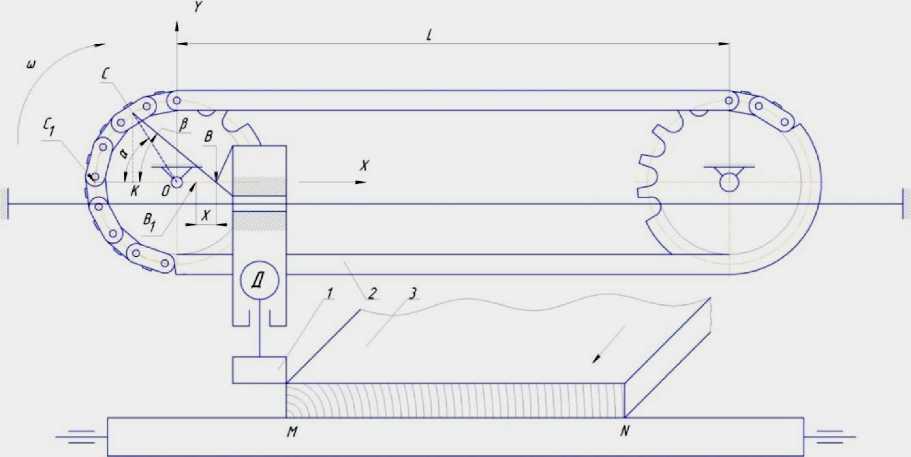
Рис. 1. Схема реализации работы цепного привода при обработке горизонтальных поверхностей: 1 – режущий инструмент; 2 – цепной привод; 3 – обрабатываемый материал

Из схемы видно, что цепную передачу в пределах поворота ведущей звездочки на один угловой шаг можно рассмотреть как плоско-рычажный механизм, в котором в данном мгновенном положении при входе режущего инструмента в крайнее положение отрезок ОС является кривошипом (длиной, равной радиусу звездочки r), а отрезок СВ – шатуном (поводком), который перемещает режущий инструмент 1 . Когда точка С при вращении звездочки находится в крайнем левом положении (точка С 1 ), инструмент перейдет в положение В 1 . При повороте кривошипа на угол α звено цепи переместится в точку С , а инструмент в точку В , при этом поводок CD составит с линией крайних точек угол β . Из рисунка видно, что перемещение х можно выразить формулой

x = r • ( 1 - cos a ) - 1 • ( 1 - cos p ) ,

где r – длина кривошипа ОС (радиус звездочки); l – длина шатуна (поводка) СВ.

В данном выражении угол β является неявным, поэтому выразим его через угол α. На схеме есть два треугольника с общим катетом СК. Находим катет СК и приравниваем его значения

r • sin a = l • sin 0.

Откуда получаем

r sin p = - • sin a . l

r

Применив правила тригонометрии sin в = у sin a , получим

cos в =

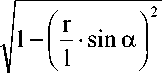
Разложим подкоренное выражение, и, отбрасывая третий член, выражение будет иметь вид

cos в = 1 -

Г г2

, И ■sin

л

a

J

Учитывая, что величины r и l по длине незначительно отличаются друг от друга, получим cos в = 1

sin² a

С учетом вышеприведенных преобразований формула перемещений инструмента будет иметь вид:

Г

x = r •Q - cos a)-1 • 1 -1 +

V

sin a

x

= r •

r

1 - cos a

• 2 A sin a

—

V

2 J

.

Знак минус перед последним членом уравнения имеет место при расчете угла α при для левого крайнего положения, если же расчет вести от правого крайнего положения, то этот знак следует поменять на положительный [3].

Скорость движения инструмента выражается уравнением dx v = — dt

= r • sin a

V

—

sin a dx

2 J

dt

.

Известно, что da      vn

— = ® = —

dt

.

r

Тогда скорость движения инструмента будет находиться как

v = v ₀ • sin a

—

V

• 2 A sin a

?

J

,

где v ₀ - окружная скорость звена цепи на звездочке.

n • n v0 =--r .

0     30

Ускорение инструмента, перемещаемого при обработке изделия на левых и правых краях, определяется как производная скорости по времени

dv /         i\da

a = — = vn • (cosa — cos2a)—.

dt 0                    dt

Подставив в выражение (13) выражение (10), получаем

v ²

a = — • ( cos a — cos 2 a ) . r

Из полученной формулы видно, что наибольшее ускорение получится в левом и правом крайних положениях и оно равно нулю, когда:

а=90°+в; 0=270°-^.

При работе цепного поступательного привода нельзя допускать изменения направления движения инструмента на обрабатываемом объекте. Такое изменение направления может вести за собой прижоги обрабатываемого материала и изменение шероховатости обрабатываемой поверхности. Поэтому в разрабатываемой схеме реализации работы цепного привода обрабатываемое изделие размещается между звездочками на ширине MN, тем самым обеспечивается выход инструмента.

Звено С цепи в крайних положениях движется по кривой траектории, описываемой уравнением

2       2      2

x 2 + y ² = г ² .

При равномерном вращении модуль скорости звена С на звездочках постоянен, и параметрическое уравнение годографа скорости имеет вид:

x = v_v = x = — k • г • sin kt. x

У = v_y = У = k ’ r ’ cos kt

Модуль полного ускорения через проекции на оси координат составит:

dv ₂

a_v = —- =- k • r • cos kt ;

x dt dv a„ = —— = -k • r • sinkt;

y dt a = a2 + a2 = k2 • r = const. xy

Полное ускорение является нормальным по направлению к О при отсутствии касательного ускорения. Ускорение режущего инструмента, присоединенного через поводок к звену, также незначительно и приведено выше.

Графики изменения кинематических параметров представлены на рисунке 2.

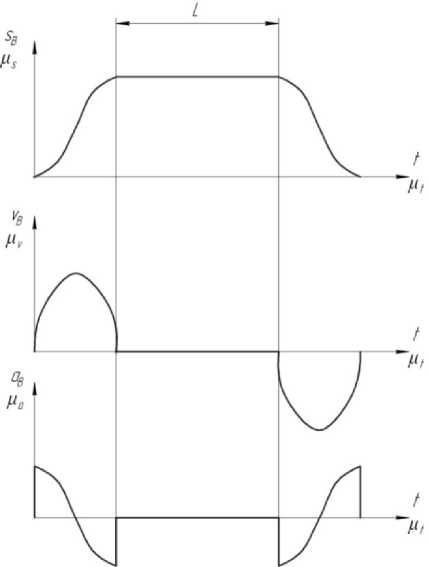
Рис. 2. Графическое изменение кинематических параметров цепного поступательного привода

Величина ускорений в крайнем левом и правом положениях при оптимальной угловой скорости звездочек в пределах 50–100 об/мин и диаметре 100 мм не превышает 10 м/с2, что позволяет перемещать значительные массы, включая обрабатывающий инструмент. Инерционные нагрузки, силы полезного сопротивления обеспечивают устойчивость поступательного привода, состоящего из цепи, звездочек, редуктора и приводного двигателя, проверенных практикой.

Выводы

• 1.    Разработана методика расчета кинематических параметров цепного поступательного привода со значительными ходами перемещений рабочего органа.

• 2.    Выполнены исследования, повышающие качество проектных решений, ускоряющих конструкторскую подготовку производства новых механизмов линейных перемещений для различных технологических процессов.