Синтез фазового транспаранта с заданной индикатрисой рассеяния

СИНТЕЗ ФАЗОВОГО ТРАНСПАРАНТА С ЗАДАННОЙ ИНДИКАТРИСОЙ РАССЕЯНИЯ

• 1,    Вывод явной формулы для функции пропускания случайного Фазового транспаранта

В рамках задачи о синтезе элементов плоской компьютерной оптики представляет интерес поиск методов синтеза фазовых элементов со случайной функцией комплексного пропускания, формирующих световые поля с заданными статистическими характеристиками.

В работе предлагается новый метод расчета случайной фазовой функции транспаранта, создающего в дальней зоне дифракции световое поле с заданным распределением средней интенсивности. Приводятся результаты численного моделирования предложенного алгоритма.

Средняя интенсивность когерентного монохроматического света в дальней зоне дифракции связана с автокорреляцией функции комплексного пропускания случайного транспаранта (диффузора) преобразованием Фурье:

<1(х)> = // G(t)exp (^ х t) d2 С,                                           (1)

S'              Z где G(t-t') = <ехр[1ф(?) - 1ф(?')]> - автокорреляционная функция чисто фазового пространственно однородного случайного поля, формирующегося сразу за диффузором с функцией пропускания, равной ехр[1ф(£)];

<1(х)> - средняя интенсивность света в дальней зоне дифракции;

• <...> - знак усреднения по реализациям статистически подобных фазовых диффузоров;

к = ^- - волновое число света с длиной волны Л;

z - расстояние от диффузора до Фурье-плоскости;

S' - область задания функции пропускания диффузора.

Из (1) для функции G(x) получается выражение

G(£) = 7 // exp(-    7С) d2x,                                       (2)

С S где С = W d2x, S - область задания требуемой интенсивности. S

Для дальнейшего потребуется ряд упрощающих предположений, необходимых для того, чтобы рассуждения можно было довести до конца. Так будем требовать нормальности распределения вероятности для фазовой функции диффузора <р(х). При этом пусть имеют место соотношения:

<<р(х)> = 0, «р³(х)> = с²,

<ф(7)ф(х')> = a3h(x - х'), которые означают, что среднее значение фазы диффузора равно нулю, дисперсия постоянная и равна о2, функция автокорреляции фазы h(x - х') зависит от разности аргументов.

Для гауссовых случайных полей известно , что автокорреляция поля ехр[1ф(х)] и автокорреляция фазы ф(х) связаны соотношением

G(7) = ехр[-о2(1 - h(7))],                                                    (3)

из которого получается выражение для функции

h(7) = 1*а In G (7) .                                                        (4)

Одну из реализаций фазы транспаранта ф(х) можно смоделировать численно с помощью некоторого преобразования исходного белого шума п(х), который задается датчиком псевдослучайных чисел. Покажем, что искомым преобразованием является следующее:

ф(7) = о У/ /< (С) n (Е) ехр (-17 С) daC.                                         <5)

S'

Действительно, так как <п(£)п(С')> = 6(£ - С), то из (5) следует, что о²К(7 - 7') = <ф(х)<р(х¹ )>- =

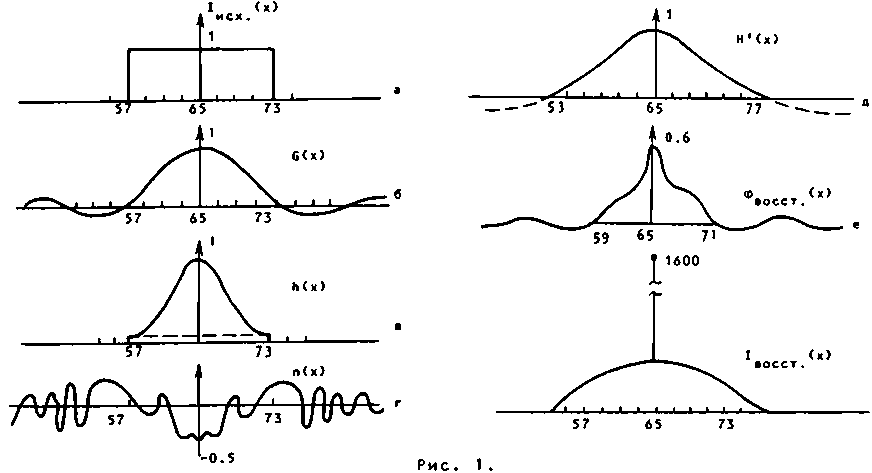
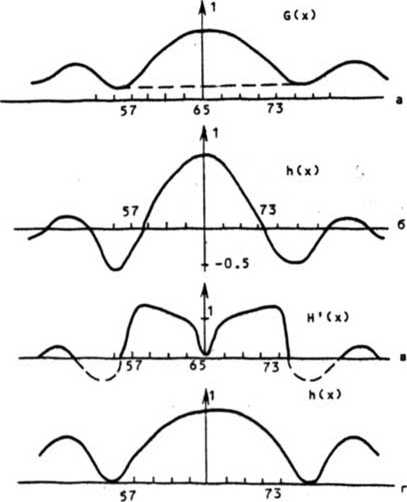
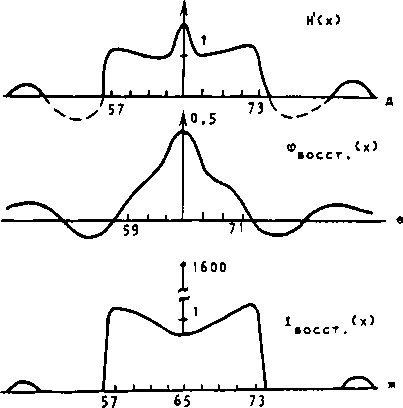
= о2 /J//[H(C)H(E,)]i

= о3// H(E)exp[i(7 - 7)E]daC.                                          <6)

S'

Из (6) следует, что функция Н(С) из (5) является обратным преобразованием Фурье от автокорреляции фазы диффузора.

Из (2), (4), (5) и (6) следует окончательное выражение для вычисления реализации фазы синтезируемого диффузора через требуемое распределение интенсивности и через реализацию белого шума:

ф(7) = о И п(Е)е"1Х^[// [1 ♦ О-2 1п[с-1// х S'                                       1 s i                                                                            C7>

X e"1x x' d2x'j}e1x' d3x"j d2 £.

• 2.    Анализ полученной формулы

Проанализируем, каким ограничениям должна удовлетворять функция средней интенсивности спектра <1(х)>, чтобы можно было применять формулу (7).

Из (3> следует, что функция 6(7) должна быть действительной и удовлетворять неравенству

О < 6(7) < 1,                                                                      (8)

причем 6(0) = 1, что следует из (2).                                           = действительность функции G(x) будет обеспечена, если потребовать четности для функции средней интенсивности спектра или в частном случае, ее радиальной симметричности. Это следует из известного факта ЧТО Фурье-Образ от четной действительной функции есть четная действительная функция. Положительную определенность          г ..

_              Н м=лс ность функции Glx) можно обеспечить, задавая функцию <1(х)> в виде

<1<7» = alo(x) + В6(7),                                                     .

Рытое С.М., Кравцов Ю.А., Физику, ч. 2. М., Наука, 1978*

Татарский В.И. Введение в статистическую радио-463 с.

где I0(x) - произвольная положительно определенная Функция;

6(х) - дельта функция.

Тогда из требования G(x) > 0 следует связь параметров а и (3 из (9) :

Р > alG . I,                                                                       (10)

о mm

• - i к - * Т ^Х2 где G (х) = $$ I (С)е       d С, G . минимальное значение функции G (х).

о           s о                          о m 1 п                                                    о

Заметим, что представления средней интенсивности в виде (9) не требуется, если она имеет гауссовый вид I ² _ ( I так как Фурье-образ от гауссовой функции есть гауссова функция.

Выбор функции интенсивности в виде (9) означает, что часть световой энергии, рассеянной на синтезированном транспаранте, не будет давать вклад в формирование требуемого распределения интенсивности, а будет собираться в нулевой пространственной частоте.

Из (8) следует условие на функцию h(x)=

Ih(x)I < 1, которое накладывает ограничения на выбор значений дисперсии фазы, но не делает этот выбор однозначным. Например, если положить

< = lln G(T)lmax'                                                           (11> то корреляционная функция фазы h(x) будет неотрицательной и будет достигать нуля в точках, где функция G(x) принимает минимальное значение. Если же, например, положить

° 2 = |ln G<^ ' |Т| -                                                                 <12)

то функция h(x) будет принимать положительные и отрицательные значения, стремясь асимптотически к нулю на бесконечности. Причем а2 > о2. Казалось бы, что лучше выбирать дисперсию фазы большую из возможных, чтобы при дифракции света на синтезированном диффузоре большая часть световой энергии попадала в область задания требуемой интенсивности. Однако численное моделирование показало, что фазы, рассчитанные по формуле (7) при а1 и О2, определенных по (11) и (12), отличаются только на некоторую несущественную постоянную. Заранее это предположить трудно, так как из приведенных ниже результатов моделирования видно (сравнить рис. 26, 2в и рис. 2г, 2д) , что вид промежуточных кривых различный для О1 и аз, хотя окончательная восстановленная интенсивность в обоих случаях одинакова (рис . 2ж) .

Так как рассмотрение ограничивается четными функциями <1(х)>, то отсюда следует, что четными и действительными будут также функции G(x), h(x) и Н(х). Из (5) следует, что для того чтобы функция фазы <р(х) была действительной, требуется также четность функции п(х), реализующей белый шум. Кроме того, из (5) следует требование неотрицательности функции Н(х). Так как неясно, какие дополнительные требования надо предъявить к средней интенсивности, чтобы гарантировать неотрицательность функции Н(х), то при численном моделировании работы алгоритма (7) все получающиеся отрицательные значения функции Н(х) заменялись нулевыми значениями. То есть вместо функции Н(х) в алгоритме использовалась видоизмененная функция Н'(х), равная

IH(x)_z H(x) > О

(13) О, Н(х) < О.

Замена, определенная в (13), приводит к искажению вида вое с тановленной функции интенсивности по сравнению с исходной заданной функцией интенсивности, но не меняет области задания интенсивности.

Заметим также, что аналогичную замену можно сделать с функцией G(x), которая должна быть положительно определенной. То есть вместо функции G(x) используется функция G'(х), равная ’б(х), G(x) > О

G'(x) =                                                                        <14)

• 5,    G(x) < О,

где б = Gm-n > 0. В этом случае не требуется задавать функцию <1(х)> в виде (9), так как алгоритм (7) при использовании замен (13) и (11») будет работать для любой исходной функции средней интенсивности.

Вид искажений восстановленной интенсивности по сравнению с исходной, которые появляются из-за использования замен (13) и (14), анализируется ниже.

• 3,    Результаты численного моделирования работы алгоритма

Численное моделирование проводилось для одномерного варианта формулы (7).

В качестве исходного распределения средней интенсивности выбиралась функция

= rect(—).                                                              (15)

а

При общем числе точек массива, равном N = 128, варьировалась ширина прямоугольника; например, на рис. 1а показана исходная требуемая интенсивность с полушириной, равной N1 = 8. На первом шаге алгоритма, в соответствии с (2), с помощью быстрого преобразования Фурье (БПФ) вычислялась автокорреляционная функция G(x), вид которой приведен на рис. 16. Далее, после замены (14) при 6= 0,07, обеспечивающей положительность функции G'(x), по формуле (4) вычислялась автокорреляционная функция искомой фазы диффузора h(x) при 6а = I In 6|, вид которой показан на рис. 1в. На следующем шаге, в соответствии с (6), вычислялось БПФ от полученной автокорреляции фазы h(x), и рассчитанная функция Н(х) подвергалась замене (13), для обеспечения неотрицательности функции Н'(х) (рис. 1г). Далее с помощью подпрограммы генерировались псевдослучайные числа п(х), равновероятно заполняющие отрезок значений [-0,5,0,5]. Эта последовательность показана на рис. 1д. На следующем шаге, в соответствии с (5), вычислялось БПФ от произведения двух полученных функций

V Н ' ( X ) П ( X ) .

Рассчитанная фазовая функция диффузора ф(х) показана на рис. 1е. Чтобы получить распределение интенсивности в спектре, которое будет давать рассчитанная реализация Фазы диффузора, вычислялось БПФ от функции ехр()ф). Полученная при этом интенсивность показана на рис. 1ж.

Из рис. |ж видно, что малая часть энергии (около IX) света, продифрагироеав -шего на рассчитанном диффузоре, дала вклад в формирование требуемого распределения интенсивности. Кроме того, замены (13) и (14), которые необходимо было осу- ществить в соответствии с требованиями к функциям, входящим в формулу (7), привели к видоизменению восстановленной интенсивности по сравнению с исходной (сравнить рис. 1а и рис. 1 ж).

Для того, чтобы не делать замену (14), воспользуемся представлением исходной интенсивности в виде (9) :

= rect(-) ♦ В6(х),                                                (16)

где 0 = 8,5, Nf = 8. Тогда корреляционная функция поля G(x), формирующего такую интенсивность, будет иметь вид, показанный на рис. 2а. Видно, что полученная функция строго положительная и необходимость в замене (14) отпадает. На рис. 26 2в показаны соответственно рассчитанные для случая (16) корреляционная функция Фазы h(x) и Фурье-образ от нее Н*(х) после замены (13) (до замены функция показана пунктиром) и при о^ = I In G(x)lx _   = I In 0,4 I.

На рис. 2г, 2д показаны рассчитанные для того же случая (16) функции h(x) и Н1(х) , но при а’ = I In Gm1nl = I Ln 0,181 .

Видно, что при различных выборах дисперсии фазы получились разного вида функции 1п(х) и Н*(х). Однако рассчитанные для обоих случаев фазовые функции оказались одинаковыми с точностью до константы, то есть ф (х) = Ф__(х) + const, ai        аа

Вид полученной функции фазы ф_о^(х) показан на рис. 2е. На рис. 2ж показан рассчитанный квадрат модуля Фурье-образа от функции ехр(1ф) или распределение интенсивности в спектре, полученное при дифракции света на фазовом диффузоре с фазой, изображенной на рис. 2е. Видно (см. рис. 2ж), что отличие восстановленной функции интенсивности от исходной заключается в подчеркивании "краев изображения" .

Таким образом, осуществление двух замен (13) и (14) при расчете фазы диффузора по методу (7) приводит к уменьшению значений восстановленной интенсивности на краях заданной области по сравнению с исходной интенсивностью (см. рис. 1ж), а осуществление только одной замены (13) приводит к увеличению значений восстановленной интенсивности на краях по сравнению с исходной интенсивностью (см.

рис. 2ж) .

Рис. 2.

Избавиться от обеих замен (13) и (14) в алгоритме (7^ можно, например, в случае гауссового вида функции исходной средней интенсивности. С целью выяснения зависимости эффекта "подчеркивания краев" в восстановленной интенсивности от вида исходной интенсивности проводилось моделирование работы алгоритма (7) в случае супергауссового вида функции IQ(x):

где L • 2-10. На рис. За показаны распределения исходной средней интенсивности для L - 2 - кривая 1, I « 6 - кривая 2, L “ 10 - кривая 3- На рис. 36 показан вид рассчитанной по (7) фазы диффузора для случая L = 1G, В = 8,5, N = 8. На Р^ис. Зв, Зг, Зд показаны исходные (кривые 1) и восстановленные (кривые 2) интенсивности в Фурье-спектре для случаев: 1=2 (рис. Зв), L = 4 (рис. Зг), L = 8 (рис, Зд). Видно, что замена (13) приводит к увеличению эффекта "подчеркивания краев" восстановленной интенсивности при увеличении L. Это связано с тем, что при увеличении L в функции Н(х) из (6) растут отрицательные значения боковых "лепестков", которые заменой (13) заменяются на нулевые значения.

На рис. 4 показаны исходная и восстановленные интенсивности при разных значениях параметра В из (9): В * 8,5 - кривая 1, В = 5 - кривая 2, 6 = 2,5 - кривая 3, при этом L ■ 4, N, « 8. Видно, что с уменьшением величины дельтаобразного пика в центре исходной интенсивности, с одной стороны, большая часть энергии попадает в область задания исходной интенсивности, но, с другой стороны, в большей степени проявляется искажение восстановленной интенсивности в виде усиления эффекта "подчеркивания краев".

Моделирование проводилось также с целью выяснения вопроса о зависимости энергии, попавшей в область задания исходной интенсивности, от величины диспер-

Из рис. 6 видно, что подбором множителя Q можно уменьшить эффект "подчеркивания краев". Видно, что при Q = 4, когда упомянутый эффект минимален (см. рис. 6, кривая 2), имеют место приближенные равенства W /W = 11%, W /Ы. - 1%. ’                                                                                    п о                р °

Видно также, что отношение Wn/WQ достигает максимума (21%) при Q = 8, при этом выполнялось примерное равенство 0<р(0)-п, минимум отношения ^- достигается при Q ■ 15, когда 0ф(0) - 2п. При 0=11 оба отношения выравниваются, то есть Wn/UQ х Wp/WQ = 17%, при этом 0<р(0) - ^ц.

• 4,    Выводы

В работе приведен метод (алгоритм) расчета фазовой функции случайного транспаранта, формирующего в дальней зоне дифракции (или в фокусе сферической линзы) заданное среднее распределение интенсивности.

Алгоритм будет работать для произвольного требуемого распределения интенсивности (описываемого четной функцией), если применять две замены (13) и (14), отфильтровывающие отрицательные значения промежуточных функций. Однако использование таких замен приводит к эффекту "сглаживания краев" восстановленной рассчитанным транспарантом интенсивности по отношению к исходной интенсивности.

Если исходная требуемая интенсивность, имея произвольный вид, содержит дель-таобразный пик интенсивности в центре, то в предложенном алгоритме можно обойтись только одной фильтрующей заменой (13), но это приводит к обратному эффекту "подчеркивания краев" восстановленной интенсивности по отношению к исходной.

Численно показано, что подбором числа, на которое нужно умножить рассчитанную фазу, можно уменьшить эффект "подчеркивания краев".

Энергия света, прошедшего- рассчитанный диффузор и попавшего в область задания требуемой интенсивности, не превышает 20% от полной энергии при дисперсии фазы меньше 2п.

МЕЖДУНАРОДНЫЙ ЦЕНТР

НАУЧНОЙ И ТЕХНИЧЕСКОЙ ИНФОРМАЦИИ подготавливает к изданию в 1991 году на русском языке сборник ПРОБЛЕМЫ ИНФОРМАЦИОННЫХ СИСТЕМ

Выпуск 11

Сборник издается Международным центром научной и технической информации.

Тематика публикуемых материалов:

• -    построение автоматизированных информационных систем,

• -    разработка перспективных направлении информационной технологии,

• -    проблемы информационного обеспечения приоритетных направлений научно-технического прогресса,

• -    методы оценки технического уровня и качества новой техники и технологий.

Сборник ориентирован на работников информационных организаций стран - членов Международного центра научной и технической информации и специалистов, разрабатывающих и использующих автоматизированные информационные системы.

Ориентировочная цена одного выпуска 4 руб.

Заказы принимаются как от учреждений и организаций, так и от индивидуальных подписчиков:

В СССР - магазином № 93 "Книга - почтой" по адресу: 117168, Москва, В-168, ул. Кржижановского, д. 14, корп. 1. Тел. 124-71-13.

В других странах - книготорговыми организациями, сотрудничающими с В/О "Международная книга". При оформлении заказов просим ссылаться на бюллетень "Новые книги СССР" (НК) № 20/1990.