Синтез фокусаторов для внутрирезонаторной коррекции тепловых искажений световых пучков

WD(r) ° апГ2П?

wr(r) = E b r2n; u n=0 n

u(r) - E Cnran.

Разность хода рассматриваемых лучей за один полный проход резонатора можно записать следующим образом:

"2(wn(0) + w_(0) +u(0)) - wn(r) - 2(w_(r) + u(r)) - w & , re[o,rJ;

AL(r) » , D         C                 °         L                               i (2)

2(w_d(0) + w_c(0) + u(0)) - 2(w_c(r) * u(r)) - w^), re]r_D,1] или, если подставить (1) в (2), в виде степенного ряда:

ДЬ(г) = Е X гзп,                                                                 (3)

п-0 п где

Хо = 0; Х„ = -а„(1 + —) - 2 СЬ +с ) , гб[0,гп]; п п М2П       П п L

Хо = а0; Х=--^- 2(Ь +с ), гб]гп,1].

п М2П       п п       J D J

После одного полного прохода через резонатор луч с координатой г в выходной плоскости придет в точку с координатой r/М. Для вычисления разности хода на следующе> проходе резонатора можно использовать формулу (3), заменив в ней координату г на r/М и т.д. После суммирования ДЬ(г) + ДЬ(^) + ... получим следующие выражения для полной разности хода рассматриваемых лучей:

Д(г) =

’ М2П

П=1 М=п-1

(%(’ * М^> + 2(bn+Cn)]r=n, re [0,rD];

Е -- —— + Ь + с т ге ]rD,1].

П—1 M2n-1 LMan П п]

Здесь rQ - радиус рассеивающего зеркала.

Определим, при каких сп на интервале ]rD, 1] (в пределах выходной апретуры резонатора) выполнено равенство Д(г) = const. Одно из решений можно получить, приравняв к нулю коэффициенты степенного ряда (4). При этом коэффициенты сп, представляющие корректирующее воздействие, связаны с коэффициентами степенных рядов для термодеформаций простыми соотношениями:

с = -а /М2П - Ь . п п'        п

Таким образом, если представить тепловые деформации в виде степенных рядов (1) , то по формуле (5) легко определить, как нужно изменить форму корректора для того, чтобы волновой фронт излучения стал плоским.

Выражение (5) для коэффициентов Сп было получено в приближении геометрической оптики. Был проведен численный эксперимент, подтверждающий эффективность использования (5) для определения формы корректора. При этом учитывались дифракционные эффекты в резонаторе. Сначала решалась самосогласованная задача для расчета распределения поля в резонаторе с учетом термодеформаций зеркал. Затем тепловые деформации, полученные из решения такой задачи, аппроксимировались многочленами типа а0 + ЯчГ2 + ПаГ4, что позволяет учесть наличие в форме корректора аберраций типа дефокусировки и сферической аберрации. С помощью (5) рассчитывалась форма корректирующего профиля, после чего решалась самосогласован ная задача для поля в резонаторе, вогнутое зеркало которого имеет асферический профиль, рассчитанный для коррекции заданных искажений. Получены следующие результаты.

Если аппроксимировать точные распределения wD(r) и w^tr), найденные из решения самосогласованной задачи, то использование в резонаторе корректора позволяет практически полностью устранить влияние термодеформаций. На рисунке приведены распределения интенсивности и фазы в плоскости перед выходным зеркалом резонатора, полученные для телескопического резонатора с увеличением М = 2.5 и эквивалентным числом Френеля Ng = 5.5. Кривые 1 получены для не возмущенного резонатора. Кривые 2 соответствуют резонатору, деформированному вследствие нагрева, когда сумма максимальных прогибов в центре зеркал составляет величину w^, - 1.82 дл. волны. Соответствующие распределения для резонатора с асферическим корректирующим зеркалом показаны кривыми 3, которые практически полностью совпадают с кривыми 1 для недеформированного резонатора. При этом фактор Штреля, характеризующий расходимость излучения, St = 1.02. Под фактором Штреля понимали отношение пиковой интенсивности на оси в фокусе линзы, расположенной на выходе деформированного резонатора, к соответствующему значению для невоэмущенного резонатора со сферическими зеркалами.

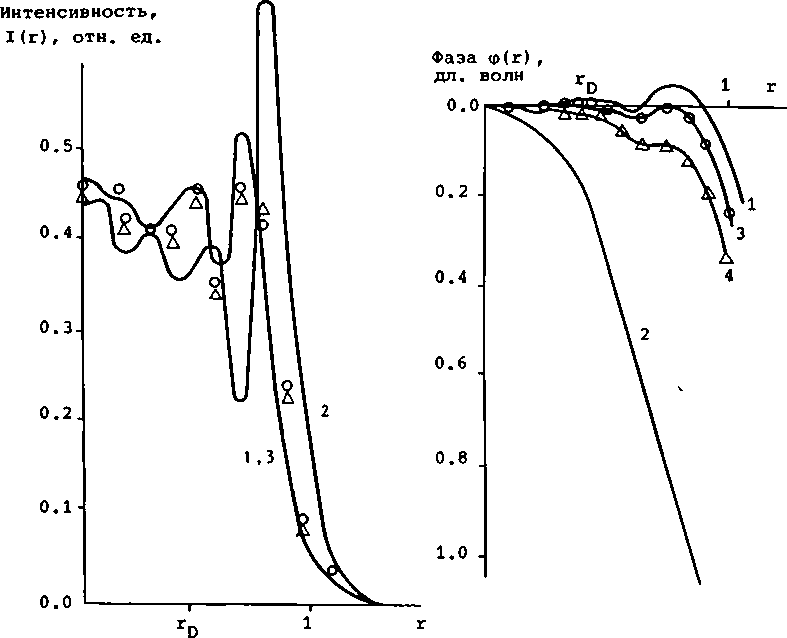
а                                          б

О - кривая 3;

д _ кривая 4

На практике получить точную информацию о распределениях тепловых деформаций зеркал резонатора довольно сложно. Ориентируясь на практически доступные данные, подход к расчету формы корректора можно несколько изменить. Были рассмотрены два случая.

В одном случае термодеформации обоих зеркал рассчитывались по распределению интенсивности в плоскости выходного зеркала, полученному из решения самосогла- сованной задачи, а в другом - на поверхности выходного зеркала задавалось равномерное распределение интенсивности, значение которой равнялось средней интенсивности в пределах выходной апертуры. Удалось увеличить фактор Штреля по сравнению с деформированным резонатором (St = 0.065) в первом случае до St = 0.98, а во втором - до St = 0.93. Соответствующие распределения интенсивности и фазы выходного излучения показаны на рисунке кривыми 3 и 4. Проведенные исследования показали, что, имея информацию о распределении поля в деформированном вследствие нагрева резонаторе, можно в приближении геометрической оптики определить форму корректирующего зеркала, использование которого внутри резонатора позволяет существенно улучшить выходные характеристики излучения .

ЛИТЕР

• 1.    Воронцов М.А., Шмаль оптики. М.: Наука, 1986. 336 с.

• 2.    Бородина И.А., Ворон кал резонатора на пространственную ции II Оптика атмосферы, 1988, т. 1

А Т У Р А г а у з е н В.И. Принципы адаптивной ц о в М.А. Влияние термодеформаций зер-структуру излучения. Методы компенса-, W 2, с. 79.

А.Я. Березний, И.Н. Сисакян