Синтез фокусаторов излучения в плоскую область в условиях нелинейных искажений световых пучков

u(x, у) = E unSn(x, y),                                                         (5)

n=i где Sn(x, у) - некоторая система функций, описывающая аберрации оптической сис темы, а коэффициенты {un)n = i являются управлениями. Таким образом приходим к задаче минимизации

J ( {un})-inf , (un} для решения которой воспользуемся градиентным методом [4], состоящим в построе k kN нии последовательности управлений u = {ип}п=1, минимизирующих функционал J, по правилу

k+i и

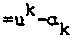
Шаг метода

^<А.

к+1 к а^ выбирается из условия убывания функционала J(u )

а градиент — = шений

{j}^ функционала J с учетом (1)-(5) определяется из соотно-dUn П=1

^- = -1т/Ф(х, у, 0)А(х, у, 0)S (х, y)dxdy, n=l,N dun Я                        “

где 4’=V(x, у, z) - решение задачи, “сопряженной" к (1)-(4)

21 П + ^ + RTV + 21RA*G=0, ЧЧЭОк(0, zO)=0,

^ + im(VA)=0, GI_x=d=0,

VIz = zo=4 (I(х, у, Z°)-I3T_(x, у) )А*(х, у, z°).

Остановимся на результатах численного моделирования. В качестве начальной амплитуды Ао в (4) было взято гипергауссово распределение

А0(х, у)=ехр{^(ха+уа)э}.                                                     (8)

Выбор Ао (х, у) вида (8) обеспечивает выполнение граничного условия (3) с достаточной степенью точности. В разложении фазы и(х, у) в (5) использовались полиномы Цернике (Z (х, у)}» п=1,21, которые представляют собой систему функций, п ортогональных в единичном круге, и описывают классические аберрации оптических систем. Длина трассы z°=0,3. Распределение интенсивности 1эт (х, у) в плоскости приемной апертуры при z=z° совпадало с |А0(х, у)1а, то есть требовалось найти фазовую функцию и(х, у) фокусатора, обеспечивающего при z=z° наилучшую компенсацию искажений начального профиля интенсивности оптического излучения, распространяющегося в нелинейной среде.

При численной реализации градиентного метода (6)-(7) для решения прямой и сопряженной задач были использованы нелинейные чисто неявные проекционно-раз-ностные схемы, для разрешения которых на каждом расчетном слое по z использовались итерации в сочетании с алгоритмом быстрого преобразования Фурье. Вопросы устойчивости и сходимости этих схем рассматривались в [5]. Результаты оптимизации по методу (6)-(7) для случая R=-20 иллюстрируются на рисунке (а-г). На рис. а представлено начальное распределение интенсивности |Ао(х, у)|а. Профили интенсивности I (х, у, z°) для начального приближения управления и после оптимизации изображены на рисунках б, г. При этом целевой функционал J уменьшился на 44^. Характерный профиль полученной фазовой функции в пределах единичного круга представлен на рис. •. Из рисунка видно, что при управлении фазой удается почти полностью скомпенсировать боковое смещение пучка, вызванное движением среды, и частично уменьшить его периферийные искажения. Полученные результаты свидетель-

Фокусировка излучения в нелинейной среде: а - начальное распределение интенсивности (z=0); б - распределение интенсивности при z=z° для начального приближения управления; в - фазовый профиль формирующего элемента; г - распределение интенсивности при z=z° после оптимизации ствуют об эффективности использования градиентных методов для расчета фокусато-ров излучения в нелинейных средах.

• 1    . Г о н ч а р ДАН СССР, 1984, т.

• 2    . Вором ц ДАН СССР, 1986, т.

• 3 . 8 о р о н ц тйеной оптики. М. :

ЛИТЕР с к и й А. В. , С 279, с. 68.

о в М . А. , М а т 290, с. 1354 .

о в М . А. , Ш м а Наука, 1985. 336

А Т У Р А и с а к я н И.Н., С в е е в А. Н . , С льгаузен с .

т е п а н о в В.В. // и в о к о н ь В.П. II

В.И. Принципы адап■

• 4.    Васильев Ф.П. Методы решения экстремальных задач. М. : Наука, 1981, 400 с .

• 5.    Разгулин А.В. Задача оптимального управления для одного нелинейного уравнения типа Шредингера // Актуальные проблемы моделирования и управления системами с распределенными параметрами: Всес. конф. (Тез. докл.). Киев, 198?, с. 34.