Синтез и исследование работы позиционной системы с линейным актуатором

Осуществление линейных передвижений посредством вращательных электродвигателей целесообразно при значительных перемещениях и больших усилиях. Для обеспечения малых и сложных движений с высокими требованиями к качеству предпочтение отдается линейным двигателям (актуаторам), подвижная часть которых интегрируется с рабочими механизмами станков, манипуляторов и т. п. устройств [ 1, 2 ] .

Применение позиционных систем с линейными актуаторами при изменении параметров силовой схемы нагрузки неизбежно ведет к трудностям формирования переходных характеристик заданного вида и проблеме демпфирования собственных колебаний [ 3-6 ] .

Одним из эффективных методов придания позиционной системе инвариантных свойств является включение в ее состав модального регулятора. При модальном управлении желательно обеспечить замыкание системы по полному вектору состояний, порядок которого равен порядку системы, и выбрать физически измеряемые переменные состояний [ 7-13 ] . Кроме того, принцип модального управления предусматривает выполнение расчета матрицы регулятора и оптимизации ее параметров. Применяемые для этих целей алгоритмы вычислений могут быть различными. Один из актуальных подходов предполагает использование процедуры синтеза замкнутой системы в пространстве состояния с помощью программного обеспечения MATLAB [14].

В данной статье представлены результаты синтеза позиционной системы электропривода с линейным соленоидным актуатором и модальным регулятором, обеспечивающим в замкнутой системе требуемые показатели качества. Новизна исследований состоит в использовании программного расширения пакета MATLAB применительно к оптимизации коэффициентов матрицы динамической обратной связи регулятора при неопределенности параметров актуатора и нелинейности нагрузки. Используемый подход дает возможность упростить процедуру синтеза замкнутой позиционной системы с модальным управлением. Моделирование и исследование электропривода с линейным актуатором позволяет проанализировать возможность его применения в качестве привода различных исполнительных механизмов при отработке малых перемещений.

Структура позиционной системы с линейным актуатором

В качестве линейного актуатора (рис. 1) используется соленоидный двигатель с возбуждением от постоянного магнита.

Катушка якоря двигателя жестко связана с рабочим механизмом. Ток якоря актуатора i_a создается преобразователем тока, использующим принцип широтно-импульсной модуляции, и измеряется датчиком тока ВА . Величина линейного перемещения X a измеряется цифровым датчиком ВL . В качестве регулятора в системе используется микроконтроллер, который вычисляет скорость перемещения V_a и реализует для управления требуемую комбинацию обратных связей.

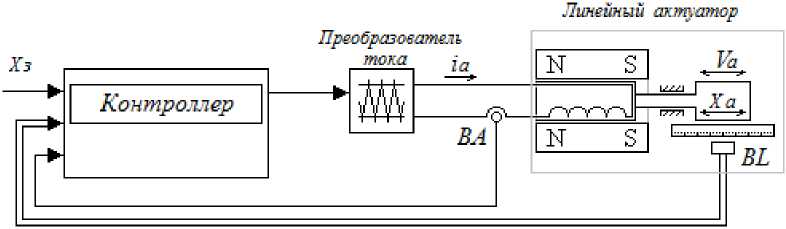
Рис. 1. Функциональная схема позиционной системы

Математическое описание позиционного электропривода

Математическое описание позиционного электропривода основывается на следующих допущениях и ограничениях: магнитная цепь актуатора не насыщена; потери в стали не учитываются; катушка якоря и рабочий механизм рассматриваются жесткой системой с ограниченным продольным перемещением.

С учетом принятых упрощений состояние разомкнутой системы электропривода характеризуется следующими уравнениями:

X ( t ) = AX ( t ) + BU ( t ); Y ( t ) = CX ( t ), (1)

тивность катушки якоря; b_m – длина магнита;

C_MW – коэффициент главной движущей силы;

LR тЭ = —; тМ = m —2— - соответственно электро-Ra        CMW

где

i

^{X (} t) = v

x

^Т Э

B = 0

А =

^Т Э

^Т М

^Т Э

K 2

K 1

^Т М

^Т М

U (t ) =

u

q

C = [ 0 0 1 ] .

Входящие в выражения (1) относительные величины и базовые постоянные определяются сле-iVX дующим образом: i = — ; v = — ; x =--отно-

I_a       V ₀        b_m

сительные величины тока, линейной скорости и

перемещения катушки якоря; q =

Q L R a C_MWU _Н

– отно-

сительная величина силы внешнего сопротивления; К = —Н ; V = H - базовые величины a 0

Ra      CMW тока и линейной скорости катушки; Fa = CMWIa -базовая величина усилия, развиваемого двигателем; UН – номинальное напряжение; Ra и Lа – соответственно активное сопротивление и индук-

магнитная и электромеханическая постоянные времени катушки якоря; m – масса катушки якоря и рабочего механизма; K 1 = C M b m R a и K 2 = —U H--

CMWUН       СMW bm обобщенные коэффициенты; CM – коэффициент реактивной силы.

Сила внешнего сопротивления движению зависит от трения скольжения. Выражение для ее расчета, полученное путем аппроксимации экспериментальных данных, имеет вид q = qо + aiv ,                                  (2)

где q ₀ = 1 и а 1 = 3,5 - 10 ^{- 3}. В процессе пуска электропривода сила сопротивления возрастает за счет составляющей пропорциональной скорости движения.

Канал обратной связи замыкается при добавлении к сигналу задания внешнего перемещения Х _З ( t ) вектора комбинации переменных состояния:

U ( t ) = Х з ( t ) - KX ( t ),                      (3)

где K = [ к 01 k ₀₂ к 03 ] - матрица коэффициентов обратной связи.

После подстановки выражения (3) в формулу (1) получаем уравнение замкнутой системы. Если внешний сигнал Х _З ( t ) = 0, то перемещение характеризуется равенством:

J X ( t ) = ( A - BK ) X ( t ), Y ( t ) = CX ( t ) .         (4)

Характеристическое уравнение замкнутой системы приобретает вид:

det[ sI - ( A - BK )] = 0,                      (5)

где I – единичная диагональная матрица.

Для обеспечения требуемых показателей качества переходных характеристик исследуемого электропривода требуется выполнить синтез регулятора, описываемого выражением U ( t ) = KX ( t ). При этом необходимо учесть, что распределение полюсов на комплексной плоскости характеристического уравнения замкнутой системы должно

Электромеханические системы соответствовать расположению полюсов стандартного характеристического полинома [ 7, 15-18 ] .

Наиболее просто процедура синтеза регулятора системы автоматического управления, рассчитывающего коэффициенты матрицы K , реализуется в пакете расширения программы MATLAB – Control System Toolbox [ 14, 19, 20 ] . При этом в качестве средства проверки управляемости замкнутой системы используется функция ctrb( A , B ), а для расчета коэффициентов матрицы K – acker( A , B , P 2).

Синтез коэффициентов матрицы обратной связи K

При синтезе позиционной системы исходим из того, что, во-первых, параметры актуатора и коэффициенты, входящие в уравнение (1), определены экспериментальным путем и имеют значения: F_H = 96 Н ; m = 0,2 кг; U _Н = 24 В; т _Э = 0,025 с; т М = 0,0002 с; K 1 = 0,685; K ₂ = 8,4; C M = 5597. Во-вторых, к системе позиционного электропривода предъявляются следующие требования: максимальная величина линейного перемещения объекта b_m = 0,04 м, время отработки заданной величины перемещения t _П = 0,01с при отсутствии перерегулирования и статической ошибке, равной А = 2 %.

Для проверки разрешимости задачи синтеза регулятора, как известно, требуется определить управляемость системы [ 15 ] . В нашем случае система является управляемой, если матрица управляемости U = [ B , AB , A ² B ] имеет полный ранг. Функция ctrb( A , B ) формирует матрицу управляемости для модели в пространстве состояний.

Задание коэффициентов матриц А и В в про- грамме Control System Toolbox пакета MATLAB выглядит следующим образом:

>> A =[–40 –40 0;9700 0 –6654;0 8,4 0];

^ В = [ - 40;0;0 ] ;

^ U = ctrb( A , B ). U =1,0 е + 007*

- 0,0000 0,0002   1,5456

0         - 0,0388 1,5520

0        0         - 0,3248

^ rank( U )

ans = 3

Результаты расчетов показывают, что ранг матрицы соответствует порядку системы. Следовательно, система управляема при использовании датчиков или наблюдателя.

Для получения заданного быстродействия при отсутствии перерегулирования в качестве стандартных полиномов выбираем многочлены H ₁ ( s ) и H ₂ ( s ) (см. таблицу), которые в отличие от биноминальных полиномов обеспечивают более высокое быстродействие, при этом по сравнению с полиномом Батеттерворта переходные характеристики не имеют перерегулирования. Результаты расчета матрицы коэффициентов приведены в таблице.

Математическое моделирование позиционной системы

Для осуществления численного моделирования динамики синтезированной системы с учетом неопределенности параметров силовой схемы и нагрузки составлена математическая модель в программе Simulink пакета MATLAB (рис. 2).

В схеме модели блок Actuator реализует систему уравнений (1), элемент Input – заданное перемещение, звено Load имитирует нагрузку, опи-

Формирование характеристического полинома и расчет коэффициентов

Вид стандартного полинома H1 (s) = s3 + 2,05to0s2 + 2,39to2s + ^0 , согласно [8] H2 (s) = s3 + 2,4to0 s2 + 2,6to2 s + to0, согласно [2] Время переходного процесса для стандартного полинома при установившейся ошибке А = 2 % и to0 = 1 т = 5 с т = 6 c Собственная частота для заданного времени переходного процесса т     5 ton = — =----= 500 1/с 0   tП   0,01 т     6 ton = — =----= 600 1/с 0   tП   0,01 Вычисление полюсов характеристического полинома замкнутой системы ^ pole( H 1) ans = 1,0 e + 002 * –3,4041 +4,9729i –3,4041 –4,9729i –3,4419 ^ pole (H2) ans = 1,0 e + 002* –5,0447+4,9658i –5,0447 – 4,9658i –4,3107 Задание вектора желаемого расположения полюсов Р2 >> P2= 1,0e +002* [–3,4041+4,9729i; –3,4041–4,9729i; –3,4419] >> P2= 1,0e +002* [–5,0447+4,9658i; –5,0447–4,9658i; –4,3107] Расчет коэффициентов матрицы K >> k1 = acker(A, B, P2) k 1 = 100* [-0,2463 - 0,00396 - 0,2078] k 1 = 100* [-0,35 - 0,0126 - 0,2078] сываемую выражением (2). В составе схемы имеется дополнительная структура – субсистема Poss.system2, предназначенная для получения сравнительных осциллограмм, отражающих изменения исследуемых параметров позиционной системы электропривода.

На рис. 3 и 4 представлены результаты исследований.

Из приведенных на рис. 3 кривых видно, что включение в систему регулирования матрицы обратных связей по состоянию обеспечивает требуемые показатели качества переходного процесса

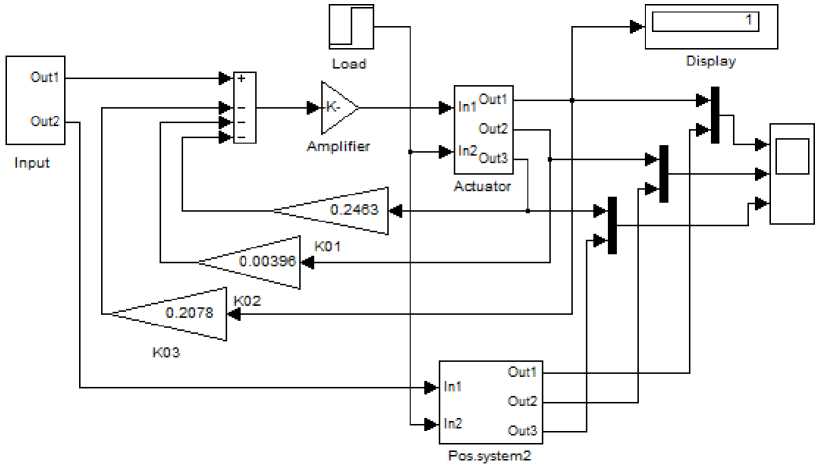
Рис. 2. Схема математической модели позиционного электропривода

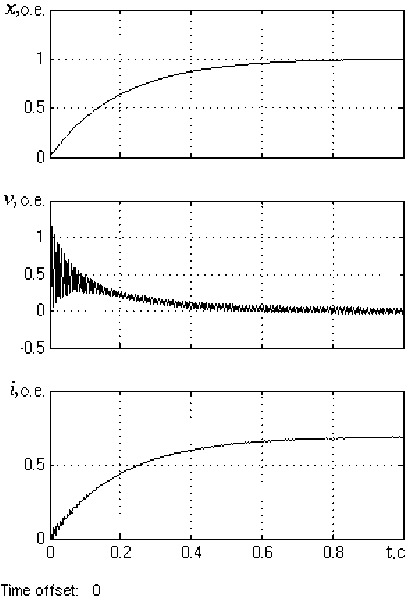
а)

Рис. 3. Переходные характеристики позиционной системы при отработке заданного перемещения:

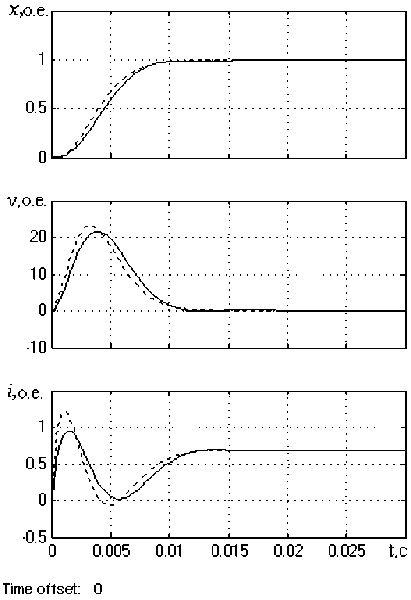
б)

а - в разомкнутой системе; б - в замкнутой системе (сплошная линия соответствует полиному H1(s), а пунктирная - полиному H2(s) )

Электромеханические системы

а)

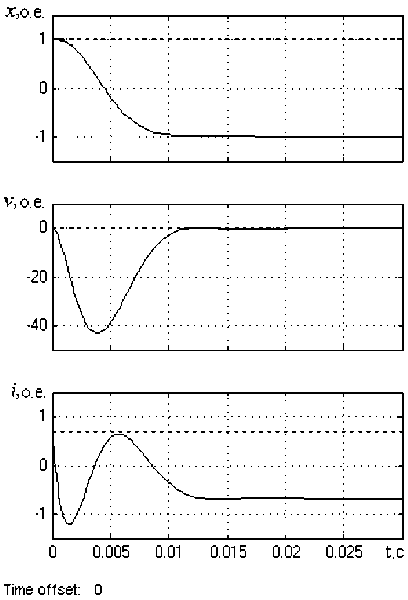
Рис. 4. Переходные характеристики позиционной системы при реверсе (а) и изменении параметров (б) (короткий пунктир соответствует изменению коэффициента усиления Amplifier, длинный пунктир – изменению нагрузки)

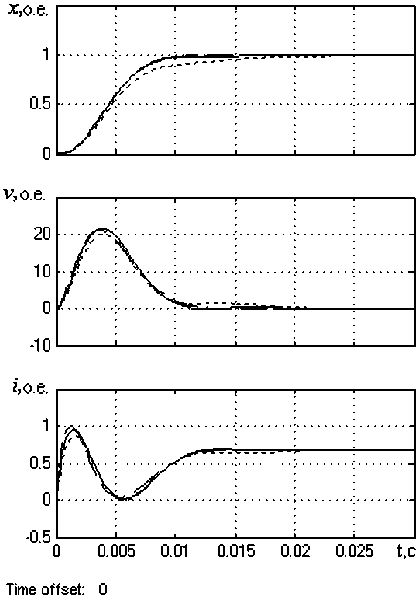
б)

при отработке заданного перемещения и его реверсе. При этом наилучшие показатели качества переходного процесса обеспечивает распределение полюсов на основе стандартного полинома H ₁ ( s ) .

Осциллограммы рис. 4, а сняты при изменении знака заданного перемещения на обратный. Они характеризуют динамические свойства позиционной системы при реверсе электропривода. Графики рис. 4, б получены при уменьшении коэффициента усиления Amplifier и величины нагрузки на 10 %. Очевидно, что при указанных воздействиях кривые переходных характеристик (см. рис. 4, б) практически не изменяются, что подтверждает инвариантность замкнутой системы к изменению параметров силовой схемы и нагрузки.

Выводы

• 1.    Предложены позиционная система электропривода с линейным соленоидным актуатором малых перемещений и методика синтеза модального регулятора с применением программного расширения Control System Toolbox пакета MATLAB, обеспечивающие апериодический характер переходного процесса рабочего механизма с заданным высоким быстродействием.

• 2.    Рассмотренная структура позиционного электропривода с линейным актуатором может быть использована для перемещения различных

рабочих механизмов при неопределенности параметров его силовой схемы и нагрузки, когда перемещение не превышает 0,04 м с точностью в 2 %.