Синтез матрицы переходных вероятностей конечной марковской цепи, описывающей процесс информационного обмена в соединении «Точка-точка» методом фиктивных состояний

Большинство сетей передачи данных (СПД) в настоящее время основано на пакетной коммутации. Для реализации заложенных в такие СПД алгоритмов функционирования сообщения, передаваемые между потребителями, фрагментируются на протокольные единицы данных, которые в общем случае называются пакетами (П). При этом в процессе доставки П возможны их искажения или потери, что приводит к снижению достоверности. Для обеспечения гарантированного информационного обмена осуществляется применение различных механизмов адаптации к условиям обстановки (помехоустойчивое кодирование, изменение интенсивности выдачи пакетов в СПД и др.), и используется обратная связь в виде отправки квитанций (Кв) на принятые пакеты [1; 2]. Таким образом, процесс доставки каждого П сообщения является случайным. Количество повторов П, Кв и временные интервалы между ними определяются конкретным протоколом информационного обмена (ИО), однако в целом изменение состояния всего процесса доведения осуществляется в дискретные моменты времени, определяемые моментами прихода П или Кв, а также выдачи их повторов. Особенностью доставки пакетированного сообщения является отсутствие у него последействия ‒ переход из состояния в состояние зависит только от того, в каком состоянии процесс находится в данный момент времени, и не зависит от того, как он в это состояние пришел. В связи с указанным распространенным научно-методическим аппаратом, применяемым для исследования вероятностновременных характеристик доставки сообщений в СПД, является теория конечных марковских цепей (КМЦ).

В общем случае процесс ИО между узлом-отправителем (УО) и узлом-получателем (УП) представляется в виде соединения «точка-точка» (СТТ) (рисунок 1) [1; 2]. В таком соединении имеется прямой канал в направлении УО-УП и обратный в направлении УП-УО. Указанные каналы имеют свои характеристики по пропускной способности и уровню помех, однако в частном случае можно считать, что эти характеристики совпадают.

В процессе доставки пакетов сообщения в СТТ имеется множество состояний, которое можно разделить на два класса։ переходные и поглощающие. К поглощающим состояниям относится состояние доведения сообщения и состояние не-доведения после возможного количества повторных передач пакетов. Это обуславливает то, что

Рисунок 1. Структурная схема СПД с соединением типа «точка-точка»

при исследовании процесса ИО используются поглощающие КМЦ.

Процесс ИО в СПД оценивается по вероятностно-временным характеристикам (ВВХ) ‒ вероятность доведения сообщения за время, не превышающее допустимое [3‒7]. Определение ВВХ с использованием теории КМЦ осуществляется на основе уравнения Колмогорова ‒ Чепмена (УКЧ):

• ( l )    ( l - 1 )

P d¹) = P d ) P [ d , d ], ⁽¹⁾ где P d ^{- 1 )} , P^ d ) - векторы вероятностей состояний ПКМЦ соответственно на ( l ‒ 1)-м и l -м шагах, d - число состояний процесса доставки П, P [ d d ] -матрица переходных вероятностей (МПВ). Элементами МПВ являются вероятности доведения (недоведения) до УП пакета ( p _п , q _п ) и Кв ( p _кв , q _кв ) на него за один повтор:

p п = ^{( 1 -} p о ) L " ,q п =^{1 -} Р п , ⁽²⁾

Р кв = ( 1 — p о ) L - q кв = 1 — p кв , (3) где p ₀ - вероятность битовой ошибки при доведении П по каналу передачи данных, L _п - длина П в битах, L _кв - длина Кв в битах.

Особенностью классической теории КМЦ [8] является то, что определение характеристик исследуемого процесса происходит с фиксированными по времени шагами. Такой подход позволяет оценить вероятность перехода случайного процесса в искомое состояние за некоторое число шагов. Однако процесс ИО в СТТ обладает особенностью, заключающейся в наличии разных по времени интервалов доведения П и Кв, а также времени ожидания повторной передачи пакета при его недоведении. Таким образом, применение одинаковых по длительности шагов не позволяет адекватно оценивать временную составляющую.

Для получения адекватных временных характеристик доставки сообщений в работе [3] предложено два метода ‒ метод среднего шага переходов и метод фиктивных состояний. Метод среднего шага основан на введении в рассмотрение понятия матрицы шагов переходов, ненулевые элементы которой показывают время перехода из одного состояния в другое. На основе данной матрицы определяется частный и общий средние шаги переходов, которые позволяют определять ВВХ в масштабе времени, приближенному к реальному. Недостатком данного метода является наличие значительной погрешности при определении временных характеристик исследуемого случайного процесса. Второй предложенный метод позволяет сократить такую погрешность за счет введения дополнительных состояний через кратный интервал времени и дальнейшего

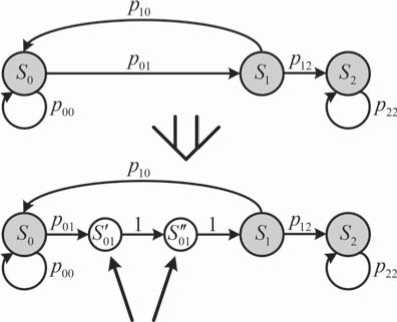
Рисунок 2. Вариант трансформации ГСП при использовании метода ФС использования классического подхода. Такие состояния названы фиктивными (ФС).

Состояние КМЦ Si называется фиктивным, если оно является невозвратным и не поглощаю- щим и имеется только один переход из состояния Si и только в состояние Sj, вероятность которого p*: *•

Количество добавляемых ФС определяется на основе некоторого нормированного шага, алгоритм определения которого следующий. Сре- ди всех шагов переходов, кроме перехода «сам в себя», выделяется наименьший, и все остальные шаги нормируются по нему. Во все переходы с

«длинными» шагами вводятся дополнительно ФС, причем их число равно норме «длинного» шага по отношению к «короткому» без единицы [3; 7]. Вариант трансформации графа состояний и переходов (ГСП) для отношения t _п/ t _кв = 3 в СПД с СТТ представлен на рисунке 2 при следующих состояниях ГСП КМЦ: S ₀ ‒ УО выдал очередной повтор П, но он УП не принят; S ₁ ‒ УП принял повтор П и выдал Кв; S ₂ ‒ УО квитанцию получил.

МПВ для такого случая преобразуется следующим образом:

р

^P [ 3,3 ]

^p 00    ^p 01

^p 10     ⁰

^p 12

^p 22

	p 00	p 01	0	0	0
	0	0	1	0	0
р P[ 5,5 ]	0	0	0	1	0
	p 10	0	0	0	p 12
	0	0	0	0	p 22

Если tп не кратно tкв, то определяется временной промежуток, равный наибольшему общему делителю (НОД) [9] tНОД для tп и tкв. Например, если tп = 0,12 си tкв = 0,08 с, то tНОД, по которому будут нормироваться все остальные шаги переходов, равен 0,04 с. При этом в рассматриваемом примере при передаче П будут образовываться два ФС, а при передаче Кв ‒ одно.

Переход в первое ФС некоторого перехода из состояния S_i в состояние S_j осуществляется с имеющейся переходной вероятностью, а переходы из одного фиктивного состояния в другое, а также из последнего ФС в искомое состояние S_j происходят с вероятностью 1. Таким образом, во всей КМЦ шаг перехода выравнивается по самому короткому шагу. Последнее позволяет использовать классический подход к нахождению ВВХ КМЦ [3‒8; 11‒14].

Постановка задачи исследования

Как правило, исследование ВВХ процесса ИО в СПД проводится с использованием специально разрабатываемых программ для ЭВМ, для чего решается задача синтеза МПВ. В свою очередь, структура МПВ и значения её элементов зависят от конкретных исходных данных. В таком случае актуальной является задача разработки правил автоматизированного синтеза МПВ. В работах В.А. Цимбала, С.Н. Шиманова, М.Ю. Попова, М.А. Лягина [3‒8; 11‒14] разработаны правила формирования МПВ для СПД с СТТ и для различных протоколов ИО. При этом в указанных работах не учитывалось влияние размеров циркулирующих в СПД пакетов и Кв на число ФС в ПКМЦ, а также изменяемое количество повторов Кв на принятый П.

В настоящем исследовании решается задача разработки правил синтеза методом ФС МПВ КМЦ для процесса ИО в СПД с СТТ, позволяющих устранить указанный недостаток.

Анализ закономерностей синтеза МПВ КМЦ

Из анализа ГСП и матрицы переходных вероятностей цепи, описывающих процесс доставки пакета сообщения в СПД с СТТ с использованием метода ФС, следует, что существует ряд закономерностей, позволяющих найти (синтезировать) все элементы МПВ. В качестве примера для иллюстрации этих закономерностей рассмотрим вариант СПД с СТТ для протокола ИО, в котором предусмотрена выдача двух повторов П (максимально) и двух повторов Кв. При этом пусть Lп = 432 бит, Lкв = 288 бит, скорости передачи прямого Vnp и обратного Vo6p каналов ПД равны 1200 бит/с. Поскольку tп = Lп/Vnp; tкв = Lкв/Vo6p, (4)

для приведенных исходных данных (ИД) L = 0,36 с и С = 0,24 с, а t™л = 0,12 с. Состо-п кв НОД яния процесса информационного обмена для рассматриваемого случая следующие։ S0 ‒ УО выдал 1-й повтор пакета; S0′1 ‒ первое ФС перехода S0 ^ S1; S0'1 - второе ФС перехода S0 ^ S1; S03 - первое ФС перехода S0 ^ S3; S0"3 - второе ФС перехода S0 ^ S3; S1 - УП получил 1-й повтор пакета и выдал квитанцию; S12 ‒ первое ФС перехода S1 ^ S2; S(9 - первое ФС перехода S1 ^ S9; S2 - УП получил 1-й повтор пакета и выдал повтор квитанции; S24 ‒ первое ФС перехода S2 ^ S4; S29 - первое ФС перехода S2 ^ S9; S3 - пакет не доведен при 1-м повторе; S34 - первое ФС перехода S3 ^ S4; S34 - второе ФС перехода S2 ^ S9; S34 - третье ФС перехода S2 ^ S9; S4 - УО выдал 2-й повтор пакета; S45 - первое ФС перехода S4 ^ S5; S445 - второе ФС перехода S4 ^ S5; S47 - первое ФС перехода S4 ^ S7; S47 - второе ФС перехода S4 ^ S7; S5 ‒ УП получил 2-й повтор пакета и выдал квитанцию; S5'6 - первое ФС перехода S5 ^ S6; S59 -первое ФС перехода S5 ^ S9; S6 - УП получил 2-й повтор пакета и выдал повтор квитанции; S68 - первое ФС перехода S6 ^ S8; S69 - первое ФС перехода S6 ^ S9; S7 - пакет не доведен при 2-м повторе; S78 - первое ФС перехода S7 ^ S8; S78 - второе ФС перехода S7 ^ S8; S78 - третье ФС перехода S7 ^ S8; S8 - пакет не доведен до УП за заданное число повторов; S9 ‒ УП довел квитанцию до УО, пакет сообщения доведен.

ГСП рассматриваемой ПКМЦ приведен на рисунке 3. На данном графе переходы процесса, время которых равно t _п , образуют два ФС, а переходы с временем t _кв - одно ФС. Переходы процесса из состояний, соответствующих недо-ведению П при повторе ( S ₃ и S ₇ ) в состояния повторной выдачи пакета сообщения или недове-дения пакета ( S 4 и S 9 ), равны nt _кв и образуют три ФС.

Формирование областей ГСП и МПВ, характеризующих передачу пакетов сообщения УО и передачу Кв на пакет УП, происходит циклически с числом периодов, равным количеству повторов П ( m ) в протоколе ИО. Число состояний ПКМЦ в таком цикле определяется, исходя из количества повторов П ( m ), Кв ( п ), длительности шагов переходов рассматриваемого процесса при передаче П и Кв ( t _{п НОД} , t _{кв НОД} ), выраженных в количестве t _НОД (в рассматриваемом случае t _{п НОД} = 3 , t _{кв НОД} = 2 ) следующим образом:

• 1)    поскольку П при повторе может быть доставлен или не доставлен до УП вследствие наличия помех в канале ПД, число ФС ПКМЦ, ха-

  

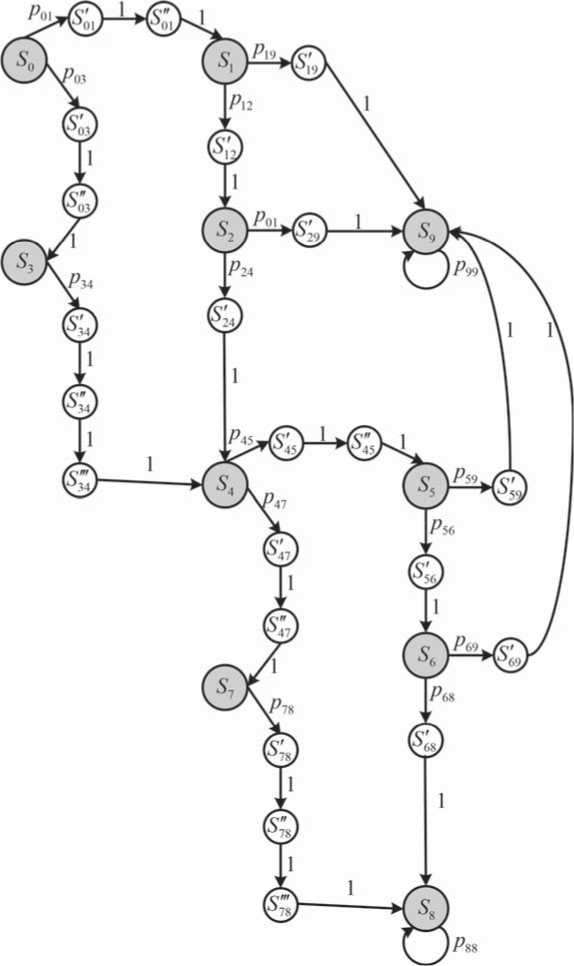
  Рисунок 3. Граф состояний и переходов ПКМЦ, описывающей процесс доставки сообщения в СПД с СТТ при двух повторах пакета сообщения и одном повторе квитанции методом ФС

  
  

рактеризующих переход процесса из состояния S0 ( S 4 ) в состояние S 1 ( S 5 ) и S 3 ( S 7 ), равно ^- t п_нод ¹;

• 2)    доставка Кв о приеме П, повторяемая УП п раз, также может быть выполнена или не выполнена вследствие воздействия помехи. Число ФС ПКМЦ, образуемых на этой фазе процесса, равно n ( ² t кв_нод ^— 1 ) ;

• 3)    переход процесса из состояния недоведения до УП повтора П сообщения S 3 ( S 7 ) в состояние повторной выдачи пакета S ₄ или в состояние не-доведения П за заданное число повторов S ₈ про-ходитчерез nt _кв _ _НОД ФС.

Учитывая это, размерность МПВ определяется выражением:

d ^— m ( 2 t п_нод + ^{3 nt} кв_нод n 1 ) + 2 , ⁽⁵⁾ где ԁ ‒ число строк (столбцов) МПВ, равное количеству состояний процесса ИО. Строки и столбцы МПВ нумеруются по порядку от 1 до d . Отсюда следует, что ненулевые индексы строк МПВ для переходов в поглощающие состояния будут равны d ( p_{d d} — 1 ) для состояния доведения П ( S 9 ) и d - 1 ( p_d - 1, _d - 1 — 1 ) для состояния его недове-дения за определенное количество повторов ( S 8 ).

Обоснование правил синтеза МПВ КМЦ методом ФС для любого количества повторов П и Кв в СПД с СТТ

Для описания правил формирования МПВ введем параметры i и ј, через которые выразим текущие состояния количества повторов П m и Кв n соответственно. Длительность шагов переходов при передаче П tп_НОД и Кв tкв_НОД выразим параметрами k и h.

Анализ ГСП (рисунок 3) показывает, что переход процесса из состояний выдачи повтора П ( S ₀ и S 4 ) в ФС S 01 и S 45 происходит с вероятностью:

p

I 1 ( 2 t п_нод + n ( 3 t кв_нод - 1 ) - 1 ) + 1, | i ( 2 t п_НОД ^{+ n} ( 3 t кв_НОД ^{- 1} ) ^{- 1} ) ⁺ 2

а переход в состояния S 03 и S 47 происходит с вероятностью:

= q п

Р

I i ( 2 t п_НОД ⁺ n ( 3 t кв_НОД ^{- 1} ) ^{- 1} ) ^{+ 1},

| i ( 2 t п_НОД ⁺ n ( 3 t кв_НОД ^{- 1} ) ^{- 1} ) ⁺ t п_НОД ⁺ n ( 2 t кв_НОД ^{- 1} ) ^{+ 1}

при 0 <  i <  m -1 . Приведенные значения индексов элементов МПВ обусловлены количеством состояний ПКМЦ в циклах, характеризующих передачу пакетов сообщения УО и передачу Кв на П получателем сообщения. Как было показано выше, это количество равно 2 t _{п НОД} + 3 nt _{кв НОД} - n -1 . Из структуры ГСП ПКМЦ следует, что в случае недоведения повтора П индекс столбца переходной вероятности (элемента МПВ) увеличивается на t п _НОД + n ( 2 t _{кв НОД} -1 ) , что обусловлено характером ИО.

В случае доведения повтора П до УП ( p _п ) выполняется переход процесса через ФС, полученные путем нормирования пакета временными отрезками t _НОД . Это происходит с вероятностью:

Р

I i (2 tп_НОД + n (3 tкв_НОД-1)-1)+1+k, | i(2tп_НОД + n(3tкв_НОД -1)-1)+2+k при 0 < i < m -1 и 1 < k < tп НОД -1. При этом показатель i показывает номер повтора П сообщения, a k перебирает все ФС переходов из S0 в S1 ииз S4 в S5 от 1 до tп_НОД -1.

Выдача повтора Кв характеризуется переходами, имеющими определенную вероятность, в состояния։

• ‒    доведения пакета сообщения ( S ₉ ) с вероятностью p _кв ;

• ‒    слeдующeй выдачи повтора Кв ( S ₂ , S ₆ ) или П ( S ₄ ) с вeроятностью q _кв ;

‒ нeдовeдeния пакeта сообщeния за опрeдeлeн-ноe количeство повторов S ₈ с вeроятностью q _кв .

При этом процeсс довeдeния П проходит нe-сколько ФС, количeство которых зависит от t _{п_НОД} и t _{кв_НОД} . При успeшной выдачe повтора Кв с вe-роятностью p _кв пepeходныe вeроятности МПВ при 0 <  i <  m -1 , 0 <  j <  n - 1и1 <  h <      - 2

кв_НОД будут имeть вид:

Р

I i ( 2 t п_НОД ^{+ n} ( ³ t кв_НОД ^{- 1} ) ^{- 1} ) ⁺ j ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ^{+ 1} | i ( ² t п_НОД ^{+ n} ( ³ t кв_НОД ^{- 1} ) ^{- 1} ) ^{+ j} ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ^{+ 2}

p кв

для переходов S 1 ^ S 1 ' 9 ,   S ₂ ^ S 29 , S 5 ^ S 59 и

• ^S 6 ^ ^S 69 ^;

Р                                  = 1

I i ( ² t п_НОД ⁺ n ( ³ t кв_НОД ^{- 1} ) ^{- 1} ) ⁺ j ( ² t кв_НОД ^{- 1} ) ⁺ h ⁺ t п_НОД ^{+ 1}, I

| i (2 tп_НОД + n (3 tкв_НОД -1)-1)+j (2 tкв_НОД -1)+ h+tпНОД +2 J для переходов в следующие ФС, при tкв НОД > 2;

p

( i ( ² t п_НОД

⁺ n ( ³ t кв_НОД ^{- 1} ) ^{- 1} ) ^{+ j} ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ⁺ t кв_НОД

= 1

для переходов S 1' ₉ ^ S 9 , S 29 ^ S 9 , S 5'9 ^ S 9 и ^S 69 ^ ^S 6 , ^при t кв_НОД > 1 ;

i ( ² t п_НОД ^{+ n} ( ³ t кв_НОД 1 ) 1 ) ⁺ j ( ² t кв_НОД 1 ) ⁺ t п_НОД ⁺ t кв_НОД

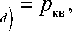
= 0

Р f-(2t

I i ( ² t п_НОД

I i ( ² t п_НОД

^{+ n} ( ³ t кв_НОД ^{- 1} ) ^{- 1} ) ^{+ n} ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД , ^{+ n} ( ³ t кв_НОД ^{- 1} ) ^{- 1} ) ⁺ n ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ^{+ 1}

для переходов S 1 '₉ ^ S 9 , S 29 ^ S 9 , S 5'9 ^ S 9 и

^S 69 ^ ^S 6 , при t кв_НОД = ¹ •

При нeдовeдeнии повтора Кв (qкв) до УО и пepeходe рaссматривaeмого процeсса в состояния слeдующeй выдачи повторов Кв или П, а такжe в состояниe нeдовeдeния П сообщeния за опрeдe-лeнноe количeство повторов S8 пepeходныe вe-роятности МПВ при 0 < i < m -1, 0 < j < n -1 и

1 <  h <  t _{кв НОД} -1 будут иметь следующий вид:

^| i ( ² t п_НОД ^{+ 3 nt} кв_НОД ^- n ^{- 1} ) ^{+ j} ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ^{+ 1}, | i ( ² t п_НОД ^{+ 3 nt} кв_НОД ^- n ^{- 1} ) ^{+ j} ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ^{+ 1}

q кв

для переходов S 1 ^ S 1' ₂ , S ₂ ^ S 24 , S 5 ^ S 56 и ^S 6 ^ ^S 68 ^;

i ( ² t п_НОД ^{+ 3 nt} кв_НОД ^- n ^{- 1} ) ^{+ j} ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ⁺ t кв_НОД ^{+ h} , i ( ² t п_НОД ^{+ 3 nt} кв_НОД ^- n ^{- 1} ) ^{+ j} ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ⁺ t кв_НОД ⁺ h ^{+ 1}

= 1

для переходов S 1₂ ^ S ₂ и S 56 ^ S ₅ ;

p

| i ( ² t п_НОД ^{+ 3 nt} кв_НОД ^- n ^{- 1} ) ⁺ n ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД , |⁽ i ^{+ 1 )} ( ² t _п _нод ^{+ 3} nt кв_НОД ^- n ^{- 1} ) ^{+ 1}

при t кв_НОД > ¹ и

^I i ( ² t п_НОД ^{+ 3} nt кв_НОД ^{- n - 1} ) ^{+ n} ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД , |⁽ i ^{+ 1 )} ( 2 t п_нод ^{+ 3} nt кв_НОД ^- n ^{- 1} ) ^{+ 1}

= qKB кв

при t _кв _ _НОД = 1 для переходов S 24 ^ S 4 и S 68 ^ S 8 .

В случae нeдовeдeния повтора П пepeход ис-слeдyeмого процeсса из ФС S ₀₃ в состояниe S ₄ и из ФС S ₄₇ в состояниe S ₈ :

S' ^ S" ^ S ₇ ^ S' ^ S" ^ S '' ^ S

47       47       7       78       78       78       8

происходит с вeроятностями, равными 1.

Индeксы этих пepeходных вeроятностeй имe- ют вид:

i ( ² t п_НОД ^{+ 3 nt} кв_НОД ^- n ^{- 1} ) ⁺ n ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ⁺ k , i ( ² t п_НОД ^{+ 3 nt} кв_НОД ^- n ^{- 1} ) ⁺ n ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ⁺ k ^{+ 1}

= 1

при 0 <  i <  m -1 , 1 <  k <  t _{п НОД} для переходов

S 03 ^ S 03 ^ S 3 ^ S 34 и S 47 ^ S 47 ^ S 7 ^ S 78 ;

p

| i ( 2 t п_НОД + 3 nt кв_НОД - n - 1 ) + n ( 2 t кв_НОД - 1 ) + t п_НОД + h -

^ i ( 2 t п_НОД + 3 nt кв_НОД - n - 1 ) + n ( 2 t кв_НОД - 1 ) + t п_НОД + h + 1

при 0 <  i <  m -1 , 1 <  h <  nt _{кв Н0Д} -1 для переходов ^О 34 ^ о 34 ^ ° 34 ^ ° 4 и ° 78 ^ ° 78 ^ ° 78 ^ ° 8 .

Параметры k и h при этом в каждом повторе П перебирают значения от 1 до t _{п_НОД} и от 1 до nt _{кв НОД} -1 соответственно, учитывая таким образом все ФС, полученные путем нормирования времени переходов интервалом времени t _НОД .

Таким образом, получены все формулы, позволяющие автоматизировать синтез МПВ, полученной по ГСП ПКМЦ с ФС, для произвольного количества повторов П и Кв в протоколах ИО в СПД с СТТ. При этом размеры пакетов сообщений и квитанций могут быть также произвольны- ми.

Правила синтеза МПВ методом ФС для любого количества повторов П и Кв

Алгоритм синтеза МПВ для процесса доставки пакета сообщения в СПД с СТТ с использованием метода ФС следующий:

Изменяя 0 <  i <  m - 1 , 0 <  j <  n - 1 , 1 <  k < <  t _п _ _НОД -1 , 1 <  h <  t квнод - 2 , вычисляем ненулевые элементы МПВ по следующим правилам.

Правило 1:

Для t кв нод > 2 при 0 <  i <  m -1 , 0 <  j <  n -1 и ¹<  h <  t ^кв_^{НОД -} 1 .

Правило 7:

p                                           — 1,

( i ( ² t п_НОД ⁺ n ( 3 t кв_НОД - 1 ) ^{- 1} ) ⁺ j ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ⁺ t кв_НОД , d )

если t кв_НОД > 1 ;

p,,                      ,                              ^ — p _кв ,

( i ( ² t п_НОД ^{+ n} ( 3 t кв_НОД ^{- 1} ) ^{- 1} ) ^{+ j} ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ⁺ t кв_НОД , d )

если t      ——^{1 .}

Правило 8:

P \ i                          .^ — 1

¹ i ( ² t п_НОД ^{+ 3} nt кв_НОД ⁿ 1 ) ^{+ j} ( ² t кв_НОД 1 ) ⁺ t п_НОД ⁺ t кв_НОД ⁺ h , I

(i(2 tп_НОД +3 ntкв_НОД - n-1)+j(2 tкв_НОД -1)+tп_НОД + tкв_НОД + h+1J при 0 < i < m -1, 0 < j < n -1 и 1 < h < Lr Hnn -1. кв_НОД

Правило 9:

P(i                   X           \         — 1 ,

I i ( ² t п_НОД ^{+ 3} nt кв_НОД - ^{n - 1} ) ^{+ n} ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД , I

^(i+1)(2tп_нод +3ntкв_Н0Д -n-1)+1                    J если tкв_НОД > 1 и

P

I i ( ² t п_НОД ^{+ 3 nt} кв_НОД - ^{n - 1} ) ^{+ n} ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД , ^ ( i + 1 ) ( 2 1 п__НОД ^{+ 3} nt кв_НОД - ⁿ - 1 ) + 1

если t, _Hnn — 1 при 0 <  i <  m -1 и 0 <  j <  n -1 . кв_НОД

Правило 10:

^¹ i ( ² t п_НОД ^{+ 3 nt} кв_НОД - n ¹ ) ' n ( ² t кв_НОД ¹ ) ' t п_НОД ^{+ k} , ^ i ( ² t п_НОД ^{+ 3 nt} кв_НОД - n ^{- 1} ) ⁺ n ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ^{+ k + 1}

—1

p

I i ( 2 t п_НОД + n ( 3 t кв_НОД - 1 ) - 1 ) + 1.

^ i ( 2 t п_НОД ⁺ n ( 3 t кв_НОД -O- ¹^²

при 0 <  i <  m -1 .

Правило 2:

при 0 <  i <  m -1 и 1 <  k <  t _{п Н0Д} -1 .

Правило 11:

p

| i ( ² t п_НОД ^{+ 3} nt кв_НОД - n ^{- 1} ) ⁺ n ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ^{+ h} ,

^ i ( ² t п_НОД ^{+ 3 nt} кв_НОД - n ^{- 1} ) ⁺ n ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ^{+ h + 1}

—1

Pf,

I i ( 2 t п_НОД ⁺ n ( 3 t кв_НОД - 1 ) - 1 ) + ¹,

^ i ( 2 t п_НОД ⁺ n ( 3 t кв_НОД ^{- 1} ) ^{- 1} ) ⁺ t п_НОД ⁺ n ( 2 t кв_НОД ^{- 1} ) ^{+ 1}

при 0 <  i <  m -1 .

Правило 3:

P₍,       /               ^= 1

I i ( 2 t п_НОД ⁺ n ( 3 t кв_НОД - 1 ) - 1 ) + 1 + k , I

^i(2tп_НОД + n(3tкв_НОД -1)-1)+2+k J при 0 < i < m -1 и 1 < k < tп НОД -1.

Правило 4:

P i

| i ( 2 t п_НОД ⁺ n ( 3 t кв_НОД ¹ ) ¹ ) ' j ( 2 t кв_НОД ¹ ) ' t п_НОД ^{+ 1}

I i ( 2 t п_нод ⁺ n ( 3 t кв_НОД 1 ) 1 ) ' j ( 2 t кв_НОД ¹ ) ' t п_НОД + 2

p кв

при 0 <  i <  m -1 и 0 <  j <  n -1 .

Правило 5:

p

| i ( ² t п_НОД ^{+ 3 nt} кв_НОД ^- n ¹ Г j ( ² t кв_НОД ¹ ) ' t п_НОД ^{+ 1}

( i ( ² t п_НОД ^{+ 3 nt} кв_НОД ^- n ¹ ) ' j ( ² t кв_НОД ^{- 1} ) ⁺ t п_НОД ⁺ t кв_НОД ^{+ 1}

при 0 <  i <  m -1 и 0 <  j <  n -1 .

Правило 6:

P

I i ( ² t п_НОД ⁺ n ( 3 t кв_НОД ^{- 1} ) ^{- 1} ) ⁺ j ( ² t кв_НОД ^{- 1} ) ^{+ h +} t п_НОД ^{+ 1},

^ i ( ² t п_НОД ^{+ n} ( ³ t кв_НОД ^{- 1} ) ^{- 1} ) ⁺ j ( ² t кв_НОД ^{- 1} ) ^{+ h +} t п_НОД ^{+ 2}

при 0 <  i <  m -1 , 1 <  h <  t квнод -1 .

П^равил°1²,: P l - , d ) ^{— P}v- 1 , d - 1 ) ^— * •

Правило 13: Все остальные элементы МПВ равны 0.

Сформулированные выше правила 1 и 2 описывают закономерности заполнения строк 1 и 16 ненулевыми элементами ( p _п , q _п ). Исходя из выражений (2), сумма элементов этих строк равна 1. Правила 4 и 5 описывают закономерности заполнения строк 4, 7, 19, 22 ненулевыми элементами ( p _кв , q _кв ). Сумма элементов строк 4, 7, 19, 22 равна 1 (3). В строках 31 и 32 размещены ненулевые элементы, обозначающие переход процесса из поглощающих состояний в эти состояния, равные 1. Остальные элементы строк МПВ, выражающие вероятность перехода из одного ФС в другое, а также из последнего ФС в другое (не фиктивное) состояние процесса, располагаются по одному в строке и равны 1. Таким образом, сумма элементов каждой строки МПВ равна 1. Поэтому матрица, синтезируемая по изложенным правилам, содержит в каждой строке вероятности

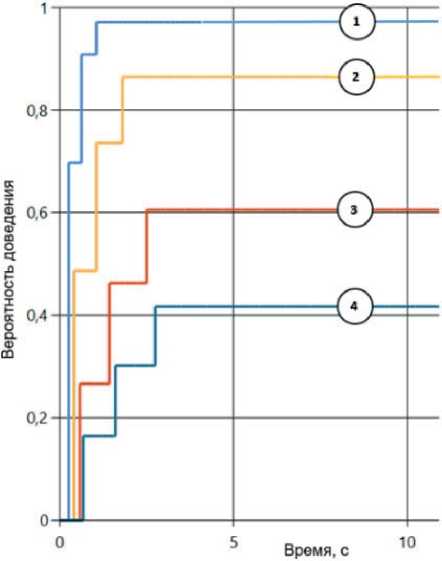
Рисунок 4. Зависимости вероятности доведения П от времени, полученные для случаев։ а ‒ классического подхода; б ‒ с применением метода ФС

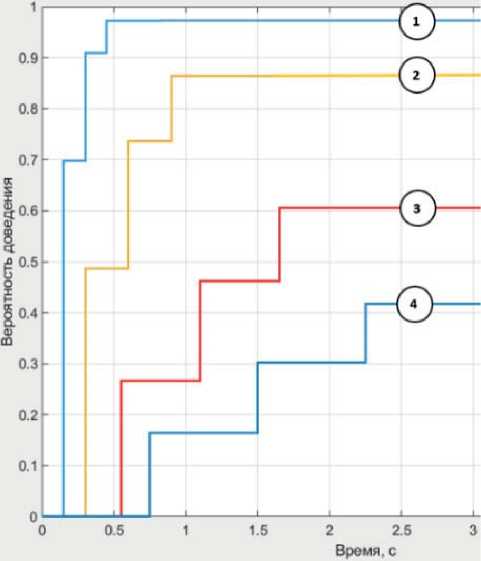
б

переходов, образующие полную группу событий, что подтверждает ее адекватность.

Проведем сравнение классического подхода к оценке ВВХ с рассмотренным выше методом ФС. Для этого выполним расчет ВВХ доставки пакета сообщения в СПД с СТТ без нормирования исследуемого процесса единым шагом перехода t _НОД [3] и с использованием метода ФС при V пр = V обр =1200 бит/с, т = 3, п = 1, p 0 =0 , 002 для размеров П и Кв։

‒ размер пакета сообщения, [бит] ‒ вариант 1 ‒ 120; вариант 2 ‒ 240; вариант 3 ‒ 440; вариант 4 ‒ 600;

‒ размер квитанции, [бит] ‒ вариант 1 ‒ 60; вариант 2 ‒ 120; вариант 3 ‒ 220; вариант 4 ‒ 300.

Полученные зависимости вероятности доведения П от времени показаны на рисунке 4. Номера построенных кривых соответствуют номеру варианта ИД.

Разработанные правила применимы к синтезу МПВ при математическом моделировании на базе теории КМЦ процесса доведения пакета в СПД с СТТ, использующей протокол типа Х.25, при произвольном размере П и Кв, а также при различном количестве их повторов. Использование изложенного в статье подхода позволяет при нахождении ВВХ формировать МПВ без разработки таблиц состояний и построения ГСП КМЦ, что упрощает его программную реализацию на ЭВМ и, соответственно, процесс расчета.

Заключение

В результате проведенных исследований установлено следующее.

• 1.    Актуальность научной задачи разработки правил синтеза МПВ для метода ФС обусловлена потребностью адекватного описания с его помощью реальных случайных процессов с дискретным временем и счетным числом состояний.

• 2.    Синтез правил формирования МПВ с использованием метода ФС базируется на выявленных в настоящем исследовании закономерностях, что позволило разработать инвариантные правила для любого количества повторов пакета и квитанции, а также при произвольном соотношении их размеров.

• 3.    Изложенный подход к расчету ВВХ ИО позволяет автоматизированно формировать МПВ, что позволяет оперативно находить характеристики доведения сообщений в СПД с использованием ЭВМ.