Синтез наноструктур на поверхности твёрдых тел в поле лазерного излучения слабой интенсивности

planar structures.

В последние годы значительный интерес исследователей вызывают поверхностные явления, протекающие под действием лазерного излучения. Такое внимание вызвано тем, что в поле действия лазера возможно создание наноструктур различных конфигураций на поверхности металлов, полупроводников и диэлектриков. Результаты исследований связаны с перспективами их широкого использования в микро-, опто- и акустоэлектронике. Однако при исследовании процессов в поле лазерного излучения часто речь идет о таких условиях, когда имеет место высокотемпературный нагрев материала, в резуль- тате чего его поверхность становится гофрированной.

Так, один из возможных способов получения обратимых и необратимых «периодических» структур на поверхности твердых тел в результате лазерной абляции тонких пленок был исследован в работах [6; 11–12; 15]. В числе прочих был проведен эксперимент по образованию упорядоченных микроструктур при абляции твердых мишеней (медь, латунь, вольфрам, бронза) толщиной 1–2 мм, находящихся под слоем жидкости (дистиллированная вода, 95%-ный этанол) [12]. Плотность энергии на поверхности мишени достигала величины 30 Дж/см2, а диа-

ВЕСТНИК Мордовского университета | 2014 | № 1-2

метр сфокусированного пятна составлял 10–60 мкм. При этом период возникающих микроструктур увеличивался в линейной зависимости от увеличения диаметра пятна лазерного излучения на поверхности мишени. Кроме того, в указанной работе предложено три различных механизма абляции:

• 1)    испарение тонкой пленки при нагреве лазерным излучением;

• 2)    взрывное удаление пленки вследствие резкого повышения давления газа, возникающего на ее границе с подложкой;

• 3)    двухфазное удаление пленки при испарении материала с поверхности и вытеснения жидкости давлением паров.

Периодические структуры, описанные в работе [Там же], образуются в результате выноса вещества мишени в виде наночастиц в жидкость. В то же время в аналогичном исследовании [11] описаны наноструктуры, формирующиеся из первоначальной шероховатости поверхности мишени под действием давления паров жидкости, окружающей мишень. Пластинка серебра, погруженная в воду или этанол, подвергалась облучению импульсным неодимовым лазером с длиной волны генерации 1,06 мкм, длительностью импульсов 350 пс и частотой их повторения 300 Гц. При этом на поверхности образовывался массив наноострий высотой 50–70 нм и плотностью до 1 010 см-2.

В работе [6] исследована генерация наночастиц благородных металлов (Ag и Au) при абляции металлических мишеней, изготовленных в виде пластинки из золота и серебра толщиной 100 мкм с содержанием металлов 99,99 %, в дистиллированной воде и этаноле излучением лазера на парах меди с длиной волны генерации 510,6 нм, длительностью импульсов 20 нс и частотой следования 15 кГц. Полученный в результате абляции коллоидный раствор облучался без металлической мишени лазерным пучком диаметром 30 мкм.

В то же время интерес представляет исследование процессов, при которых ла- зерное излучение не вызывает значительного разогрева вещества. В этом случае механизм воздействия лазерного излучения на вещество является нетепловым. Как правило, при этом механизм воздействия оптического поля на адсорбированные на твердой поверхности частицы объясняется безызлучательной релаксацией электронного взаимодействия атома с поверхностью, способной привести к его десорбции [2; 7–8; 10]. Другим возможным механизмом является поляризация световым полем адсорбированных частиц, в результате которой в некоторых случаях латеральное взаимодействие таких частиц является существенным [1; 3–5; 14]. В результате на твердой поверхности в области действия лазерного луча возникают неоднородные планарные структуры в виде «кратера» или «бугра» [1; 3–4]. Были подробно исследованы зависимости безразмерной поверхностной концентрации адсорбированных частиц P от безразмерного расстояния R при различных значениях, характеризующих процесс параметров как в установившемся, так и неустановившемся режимах [Там же].

Наше исследование посвящено образованию неоднородных пространственно-временных структур в адсорбционном слое на поверхности твердого тела под действием лазерного излучения относительно слабой интенсивности.

Математическая модель

Для одномерной задачи физической адсорбции частиц на однородной поверхности диэлектрика, полупроводника или металла ранее получено кинетическое уравнение, описывающее установление локального адсорбционного равновесия при неоднородном пространственном распределении интенсивности направленного на поверхность оптического излучения [14]. В случае двумерного поперечного распределения интенсивности падающего на поверхность светового излучения, обладающего осевой симметрией, уравнение записывается так [3]:

д n n a f au I

— = ^о F (r)—+ц    rN.1 + дt,             т r dr ^ dr)

r d r ( d r ) ,

где r – текущее радиальное расстояние; t ₁ – текущее время; N – поверхностная концентрация адсорбированных частиц (атомов, молекул и т. п.); F ( r ) – интенсивность потока частиц из газовой фазы на поверхность; S ₀ – коэффициент прилипания частиц к поверхности; т - время пребывания частиц в адсорбированном состоянии; ц -подвижность; D – коэффициент поверхностной диффузии; U – потенциал фото-индуцированного взаимодействия между адсорбированными частицами.

Следует отметить, что в данном случае величины ц и D предполагаются константами ввиду того, что взаимодействие лазерного излучения с веществом имеет нетепловой характер. Пусть функция F ( r ) задается гауссовым распределением:

F ( r ) = F ₀exp ( - r ²/Л ? ) , ⁽²⁾

где А , - эффективный радиус потока частиц, направленных на поверхность твердого тела.

Согласно работе [3], мгновенное значение потенциальной энергии фото-индуцированного диполя в локальном электрическом поле Еloc описывается следующим уравнением:

U = - dE o =- ^ o « E lOc =

= - е ^a E ² /( 1 ^- A a ) 2 (3)

где е ₀ - электрическая постоянная; a - поляризуемость отдельной адсорбированной частицы; E = |е| - напряженность электрической компоненты в электромагнитном поле лазерного излучения.

Параметр A определяет, как показано в работе [14], зависимость локального электрического поля от поверхностной концентрации адсорбированных атомов, а также от угла падения и поляризации внешнего электромагнитного поля:

E |oc = Е/( 1 - A a ) .

Локальное электромагнитное поле E =E+E состоит из внешнего поля E loc           1

и суммарного поля E1, создаваемого в точке расположения рассматриваемой частицы всеми другими фотоиндуциро-ванными диполями.

Пусть направленное на поверхность твердого тела электромагнитное поле имеет амплитуду электрической компоненты Е_о и циклическую частоту ® :

Е( t 1 ) = Е_о cos ( ® t 1 ) .

Если распределение амплитуды внешнего поля в направлении, поперечном к распространению, обладает осевой симметрией, то величина E₀ является функцией только радиуса r . С учетом этого подставим последнюю формулу в выражение для мгновенной потенциальной энергии (3) и усредним ее по периоду внешнего электромагнитного излучения. В результате получим:

U ( r ) = - e o a E о ² ( r )/ { 2 ( 1 - A a ) ² } . (4)

Приближенно можно считать, что для усредненной по времени интенсивности I оптического излучения справедлива следующая зависимость:

I ^{( r} ) = ^e o ^cE o ² ( ^r ) .

Предположим, что распределение по поперечному сечению усредненной по времени интенсивности лазерного излучения имеет гауссову форму:

I ( r ) = Ioexp (-r 7 ro2) , где r0 – эффективный радиус падающего лазерного луча; I0 – интенсивность ла-

Серия «Естественные и технические науки»

зерного излучения в точке r = 0.

С учетом двух последних соотношений запишем:

E 0² ( r ) = ” exp (^- r 7 r o ) .    ⁽⁵⁾

^e о c

Таким образом, из формул (4–5) получим следующее соотношение для определения эффективной потенциальной энергии частицы, имеющей координату r на поверхности твердого тела:

U ⁽ r ) = - 2    Aa ^6XP ' r ⁷ r o² ^

= A 0 exp (^- r²1ro ) .                       (6)

Входящий в выражение (6) коэффициент пропорциональности определяется так:

^A 0 ⁼

-

^{a I} 0

2 c ( 1 - A a ) ²

Величина A , входящая в знаменатель формулы (7), согласно работе [14] вычисляется по формуле:

ВЕСТНИК Мордовского университета | 2014 | № 1-2

-

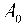
A 1

где A 1 = - a l ₀ /( 2 c ) . С учетом соотношения (2), определяющего интенсивность потока частиц на поверхность твердого тела, и формулы (6), определяющей усредненную по времени потенциальную энергию частицы в электрическом поле, являющемся суперпозицией внешнего и фотоиндуцированного электрических полей, уравнение (1) в безразмерной форме примет вид:

dn dii = exp (-R2/А2 )-n - -^^ RdR nR2 exp (-R2 )^ . (1 - nn)2 v + д +Ф „ RdR ' R ^n-l < dR J , (10) где t = ti /г , R = rko, n = N / в , в = Sо FoT , £ = 2 A цТ7, Ф = DT 7, П = 2лаР(Аr, А = А1 /r0. Дополним уравнение (10) начальным условием:

t = t о : n ( R , t о ) = n о ( R ) . ⁽¹¹⁾

В уравнение необходимо включить еще два граничных условия. Из симметрии задачи следует, что в точке R = 0 должно быть задано следующее граничное условие:

^ 1 = 0 .

d R

Оно физически означает отсутствие диффузионного потока в точку R = 0 или из нее. Кроме того, из уравнения (12) для функции U ( r ) вида (6) также следует равенство нулю дрейфовой части потока при R = 0 .

Аналогичное условие отсутствия диффузии и дрейфа адсорбированных частиц за пределы твердой поверхности зададим на внешней границе области радиуса R_F :

R = R f

^ R f n ( R f , t ) exp ( — R F ) ( 1 — n n ( R f , t ) ) 2

—

^{( R} , t )        = 0 .

Если R F >>  1 (т. е. линейный размер поверхности намного превышает эффективный радиус r ₀ лазерного луча), то граничное условие (13) может быть записано в более простом виде:

A r ® 0,6 нм коэффициент поверхностной диффузии равен D = (0,017 ^ 0,23) ■ 10 ^{— 5} m²c ^{— 1} а подвижность принимает следующее значение ц = (0,03 ^ 0,4) ■ 10 '5 m²c^lJ^l . Следует отметить, что коэффициент поверхностной диффузии и подвижность, определяемые по формулам (14), сильно зависят от температуры. Представим их в виде следующих соотношений:

^Т = ⁹ exp [ у ( 1^— V ⁹ ) ] ; (15) D ₀

Серия «Естественные и технические науки»

ф

д п ( R , t ) 5 R

R = R f

= 0 .

^- = T F T = e^xP [ Y ( 1 — 1 9 ) ], (16) ^Ц 0 TD 0

Результаты и их обсуждение

Согласно работе [14], коэффициент поверхностной диффузии и подвижность адсорбированных частиц в поле внешнего оптического излучения определяются выражениями

D = W (A r ) 2 , ц = — ,       (14)

где W = v exp [— E dif /( kT ) ] - вероятность перехода в единицу времени адсорбированного атома в соседнюю ячейку в радиальном направлении; k – постоянная Больцмана; E _dif – энергия активации диффузии; T – абсолютная температура.

Энергия активации диффузии, как правило, принадлежит интервалу Edif ® 0,01 ^ 0,1eV. Предэкспоненциаль-ный множитель v в формуле для вероятности W определим из условия hv®kT [3; 14]. Тогда, например, при температуре Т = 400 K получим v « 0,84 x1013c—’. В этом случае вероятность перехода адсорбированного атома в соседнюю ячейку составляет W = (0,46 ^ 6,3) ■ 10'2 c 1 .Следовательно, в соответствии с формулами (14) при где / = Edif /(kT,), 9 = T/T0 . Величины D0 и ц0 определяются при температуре T0. При температуре Т0 = 273 K для параметра у получим: Y = 0,4247 ^ 4,247. На рис. 1 представлены зависимости отношений DD0 и —ц0, вычисляемых по формулам (15–16) соответственно, от безразмерной температуры 9. Из рис. 1 видно, что зависимость от температуры становится сильной при более высоких значениях безразмерного параметра у .

Для безразмерных параметров ф и ^, входящих в уравнение (10), при условии, что входящие в них параметры не зависят от температуры, за исключением коэффициента поверхностной диффузии D и подвижности ц , с учетом формул (15–16) получим:

ф = T - Ф = — Ф 0 D 0 ’ Ф 0 - 0'

В данном случае величины ф ₀ и ф ₀ определяются при температуре T ₀ . Таким образом, зависимость от температуры отношений ф/ф ₀ и фф ₀ также определяется по формулам (15–16) соответственно.

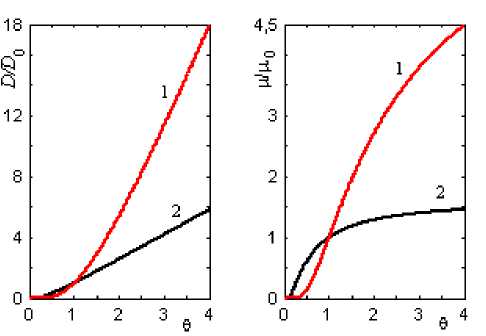
Рис . 1. Зависимости отношений (а) и (б) от безразмерной температуры при (кривые 1) и (кривые 2)

ВЕСТНИК Мордовского университета | 2014 | № 1-2

Оценим характерные значения безразмерных параметров φ и ξ . В экспериментах, описанных в работах [2; 5], сине-зеленое излучение Аr+-лазера или Не-Cd-лазера с интенсивностью соответственно 20 ВТ/см³ или 10 ВТ/см³ фокусировалось в пятно диаметром ~2мм (r₀≈1мм). В этом случае для температуры T = 400 K при τ ≈ 10 ^{- 4} c получаем φ = (0,17 ÷ 2,3) ⋅ 10 ^{- 4} . В то же время параметр τ сильно зависит от свойств поверхности конкретного твердого тела, а также от характеристик адсорбирующейся на ней частицы. Например, в случае адсорбции атомов Na на стекле τ может быть порядка нескольких секунд [2; 5]. Если принять τ = 1c , то при температуре T=400 K получим φ = 0,17 ÷ 2,3. С учетом сильной температурной зависимости, в соответствии с формулой (13), значение параметра φ в ходе экспериментов может варьироваться в достаточно широком диапазоне.

Поляризуемость α, как правило, составляет ~10-30м3. Таким образом, для параметра A1 , входящего в формулу (9), при использовании в экспериментах Аr+-лазера имеем ≈-3,3⋅10 34 J, а при использовании Не-Cd-лазера – A1 ≈-1,7⋅10-34 J . Тогда для приведенных выше значений параметров безразмер- ная величина ξ принимает значения ξ=-(0,2÷2,64)⋅10-13 в случае использования Аr+-лазера и ξ≈ -(0,1÷1,32)⋅10-13 – Не-Cd-лазера при τ = 1c . Если τ = 10-4 c , то         ξ=-(0,2÷2,64)⋅10-17         и

ξ ≈ - (0,1 ÷ 1,32) ⋅ 10 ^{- 17} в случае применения Аr+-лазера и Не-Cd-лазера соответственно.

Оценим параметр η . Величина β при τ = ( 10 ^{- 4} ÷ 1 ) c , S₀ = 0.7 и F ₀ = 10²⁰c^-1m^-2 принимает значения β = 7 ( 10¹⁵ ÷ 10¹⁹ ) m^-2 Тогда при ∆ r ≈0,6 нм и α=10^-30 м³ получим η = 0,73 ( 10 ^{- 4} ÷ 1 ) .

Очевидно, что если безразмерный параметр φ на несколько порядков превышает ξ (например, в приведенных выше оценочных вычислениях φ отличается от ξ на 13 порядков), то существенными будут эффекты, вызванные поверхностной диффузией. В то же время эффект, вызванный латеральным взаимодействием наведенных диполей, наблюдаться не будет.

При температуре T = 100K для энергий активации диффузии Edif ≈0,01 ÷ 0,1eV получим следующие значения параметров модели: ν ≈0,21×1013 c-1 и W =(0,0002÷6,6)⋅1011c-1.      Тог да при ∆r≈0,6нм, в соответствии с формулами (14), получим выражение

D =(0,00007÷2,37) ∙ 10^-7 M ² C ^-1 для коэффициента поверхностной диффузии и ц = (0,00005 ^ 1,72) ■Ю¹⁴ M ² C ^-1J ^{- 1} для подвижности. Для безразмерного параметра ф при r-1 мм и т « 10 ^{- 4} c получим ф = (0,00007 ^ 2,37) ■Ю^{- 5} . Для безразмерного параметра ^ в случае использования Аг+-лазера при т = 10 ^{- 4} c имеем ^ = - (0,000033 ^ 1,14) ■Ю^{- 17} , а в случае Не-Cd-лазера - ^ = - (0,000016 - 0,57) - 10 ^{- 17} .

Таким образом, по мере снижения температуры T с 400 до 100K отношение безразмерных параметров ф и £ уменьшается примерно в 10 раз. При температуре 100K это отношение составляет ф/ф ~10¹² . Следовательно, поверхностные диффузионные эффекты преобладают над дрейфом наведенных диполей в электрическом поле. Отношение параметров ф и £ определяется формулой:

| ф^ = ckT(al 0 . (18)

Согласно формуле (18), безразмерные параметры ф и £ сопоставимы, если:

TjI ₀ ~ ф ck = 2,42 ■Ю¹⁴ а .

Так, для характерных значений а ~ 10 ^{- 30} _м ³ 3 поляризуемости молекул получим:

T/I ₀ ~2,42 - 10 ^{- 16} K ■ m ² ■ Vt ^ч.

Последнее соотношение, следовательно, может выполняться при больших величинах 1 ₀ ~ 0,4Ы0¹⁸В_т . _м-2 при температуре T = 100 K . Однако в этом случае существенными становятся процессы, имеющие тепловой характер, а это не соответствует условиям данного исследования.

Следует отметить, что существуют молекулы с аномально высокой поляризуемостью а ~10-27м3 [9; 13]. Однако даже для таких молекул при температу- ре T = 100 K получаем ф/ф ~109, и эффект в адсорбционном слое на поверхности твердого тела, вызванный латеральным взаимодействием наведенных в адсорбированных молекулах диполей, практически не будет наблюдаться.

Однако, согласно уравнению (10), из-за наличия в знаменателе выражения ( 1 - п п ) 2 плотность дрейфового потока наведенных диполей в поле оптического излучения достигает очень больших величин при п п ^ 1 . В безразмерных величинах плотность потока, включающая диффузионную и дрейфовую части, равна:

Т Л дп

J = -ф --+ ^

5 R

nR exp( - R ²) ( 1 - П п ) 2

Серия «Естественные и технические науки»

Неоднородные поверхностные структуры образуются в результате «конкуренции» между процессами диффузии и дрейфа, выражающейся в стремлении диффузии выронить неоднородности, возникающие из-за дрейфа наведенных диполей. Пусть при пп ^ 1 в малой окрестности точки R = R0 выполняется условие J = 0 , т. е. суммарный поток отсутствует. Тогда, проинтегрировав уравнение дп = „RR exp(-R2) фдк " ^ (1 -пп)2 , получим:

ф ln x - 2 x + — + - =

I

= exP (-R02)- exP (-R2) ,(20)

= ^2

где x = п п , а соответствует точке, в которой x = п п = 1 . Исследуем равенство (20) в окрестности точки R ₀ . Разложим в ряд Тейлора левую часть неравенства (20) в окрестности x = 1 , а правую - в окрестности R = R ₀ . В результате получим следующую формулу:

n = 1/ п + exp ( — R 0²/ з )

{ 3 ^ R о ( R - R o ) ф } /л .     (21)

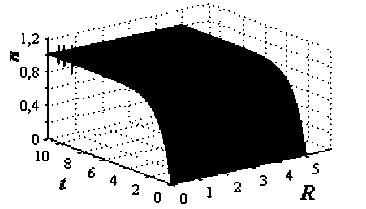
На рис. 2 представлены решения уравнения (10) с граничными условиями (12–13) и начальным условием (11) вида п (R, t0 ) = 0 при ф = -10-11, ф = 10-2, п = 0,999872, Л ^ ». Из рис. 2 (а) видно, что при заданном соотношении параметров фф = 109 с течением времени за счет диффузии на поверхности твердого тела происхо- дит выравнивание концентрации адсорбированных частиц, которая стремится к равновесному значению n=1 по мере увеличения времени t . При условии пп ^ 1 и dп/dR ^ 0 дрейфовый поток становится сравнимым с диффузионным потоком частиц и даже начинает превосходить его (рис. 2).

ВЕСТНИК Мордовского университета | 2014 | № 1-2

а

Таким образом, характер проявления латерального взаимодействия наведенных диполей в адсорбционном слое на поверхности твердого тела сильно зависит от вида адсорбированных частиц, а также свойств поверхности, на которую происходит адсорбция. Существенное влияние должна оказывать также частота из-

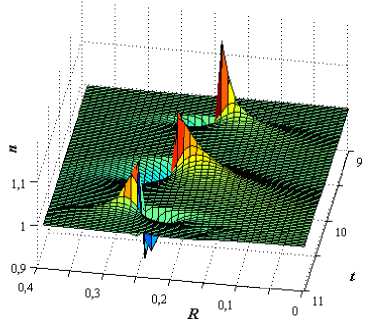
В результате возникают неоднородные поверхностные структуры в адсорбционном слое. При этом вследствие того, что в областях пространственных неоднородностей становится большой по абсолютной величине производная д п /д R , диффузионный поток начинает преобладать над дрейфовым. Формула (21) определяет на поверхности твердого тела неоднородное распределение концентрации n адсорбированных частиц в кольце с радиусом R=R₀ , в котором диффузионный и дрейфовый потоки сравнимы друг с другом. Из рис. 2 видно, что неоднородные профили концентрации адсорбированных частиц повторяются через приблизительно равные временные интервалы Л t . При этом между величинами R ₀ и Л t наблюдается линейная зависимость.

б

Рис. 2. Зависимость безразмерной поверхностной концентрации адсорбированных частиц n от радиальной координаты R и времени t (а); профиль концентрации в области пространственно-временной неоднородности (б)

лучения используемого лазера, поскольку поляризуемость а в общем случае является именно ее функцией. Знак безразмерного параметра ф определяется направлением усредненного локального электрического поля. Если оно направлено по радиусу к центру, то знак ф должен быть положительным.

Результаты проведенного анализа могут быть использованы при создании планарных структур различных конфигураций с помощью оптического излучения, например, в микроэлектронике. Их применение возможно при производстве печатных схем с высокой плотностью монтажа, а также масок для фотолитографии. Например, один из способов получения планарных структур определенной конфигурации на поверхности твердого тела заключается в изменении времени освещения лазером поверхности материала. Варьируя время действия оптического излучения, можно контролировать распределение концентрации адсорбированных на поверхности твердого тела частиц.