Синтез новых канонических структур рекурсивных цифровых фильтров второго порядка

Предлагается методика синтеза структур рекурсивных цифровых фильтров (ЦФ) второго порядка с передаточной функцией общего вида с минимальным числом узлов, блоков умножения и блоков задержки.

Постановка задачи

Известно, что цифровые фильтры с заданной передаточной функцией могут быть реализованы с помощью большого числа структурных схем [1; 6-7]. Структуры ЦФ различаются чувствительностью к точности представления коэффициентов, уровнем шумов округления результатов арифметических операций. Среди структур рекурсивных ЦФ известны так называемые канонические структуры, характеризующиеся минимальным числом блоков задержки (равным порядку фильтра) и минимальным числом блоков умножения [1]. Для ЦФ второго порядка с передаточной функцией общего вида

Рис. 2. Каноническая форма II рекурсивного ЦФ второго порядка

На рис. 1-2 и далее числами в квадрате отмечены узлы структурной схемы (входы и выход сумматоров считаются одним узлом). Очевидно, что показанные схемы характеризуются минимально возможным числом узлов – N = 4. Коэффициенты ЦФ обозначены символами c _ij , где i и j - выходной и входной узлы блока умножения, соответственно. Для структур, изображенных на рис. 1-2, справедливы равенства

H (z■) =

a o z + a z + a 2 z ² - b 1 z - b ₂

известны две канонические формы - каноническая форма I (см. рис. 1) и каноническая форма II (см. рис. 2).

⎧c 43	= a 0 ,	⎧c 21	= a 0
⎪c 42	= a 1 ,	⎪ ⎪c 31	= a 1
⎪ ⎨c 41	= a 2 ,      ⎨	c 41	= a 2
⎪c 32	=b 1 ,	⎪c 32	= b 1
⎪⎩c 31	= b 2	⎪⎩c 42	= b 2

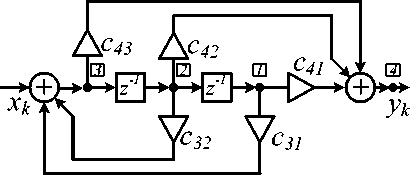
Рис. 1. Каноническая форма I рекурсивного ЦФ второго порядка

Цель статьи – ответ на вопрос, возможно ли построение других структур ЦФ с передаточной функцией (1), пятью блоками умножения, двумя блоками задержки и с четырьмя узлами.

Описание структур ЦФ топологическими матрицами

В [3-5; 7] показано, что любая структура ЦФ может быть описана топологической матрицей

.^^

T , элемент t _y которой представляет собой коэффициент передачи от узла с номером j к узлу с номером i (предполагается, что все узлы структуры ЦФ пронумерованы рядом натуральных чисел, начиная с единицы).

Работу ЦФ на структурном уровне можно описать [2; 7] разностным матричным уравнением

—*         -—- —*        -—- —*—*

Y, = TY + T,Yt , + Ix,(3)

k c k d k-1k где Yk – вектор отсчетов, вычисляемых во всех узлах ЦФ в момент времени kTs; Ts - интервал дискретизации; Tc – часть топологической мат-рицы,соответствующаяструктуреЦФ,изкоторой исключены блоки задержки; Td – часть топологической матрицы, которая определяет положение блоков задержки; T = Tc + z-1Td; I - вектор, все элементы которого равны нулю, за исключением равного единице элемента с номером inp; inp - номер входного узла ЦФ; {xk |k = 0... да} - отсчеты входной последовательности ЦФ. Взяв от (3) z - преобразование, получим выражение

Y ( z ) = T c Y ( z ) + z ^{- 1} T d Y ( z ) + I X ( z ) , (4) где X ( z ) - z -преобразование входной последовательности x _k ; Y ( z ) - вектор, компоненты которого равны Y i ( z ) - z - преобразованиям последовательностей { y _ik |i = 1... N,k = 0... да }, вычисляемых в узлах структурной схемы ЦФ.

Из уравнения (4) получим

Y ( z ) = ( E - T ( z ^{- 1} ) ) -1 I X ( z ),          ⁽⁵⁾

где E – единичная матрица. Передаточная функция ЦФ будет равна

H ( z ) = Y^,           (6)

X ( z )

где out – номер выходного узла ЦФ.

Синтез новых канонических форм на основе канонической формы I

Для схемы с элементами задержки, расположенными как в канонической форме I, топологическая матрица T в общем случае имеет вид:

	⎡0	-1 z	0	0⎤
..^^ T=	⎢c 21	0	-1 z	0⎥⎥	,           (7)
	c 31	c 32	0	0⎥⎥
	⎢⎣c 41	c 42	c 43	0⎥⎦

(для схемы, представленной на рис. 1, с ₂₁ = 0). Соответствующая структурная схема приведена на рис.3.

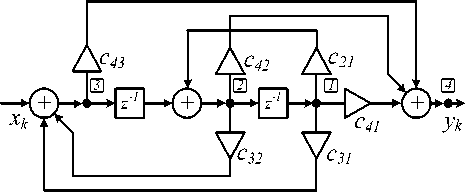
Рис. 3. Обобщенная структурная схема, соответствующая топологической матрице (7)

Система уравнений, описывающая работу схемы (см. рис. 3), имеет вид:

'Y, ( z ) = Y 2 ( z ) z ^{- 1} ,

Y 2 ( z ) = C 21 Y 1 ( z ) + Y 3 ( z ) z ^{- 1} ,

Y3 ( z) = c31Y1 (z) + c32Y2 (z) + X (z),

^Y 4 ( z ) = ^C 41 Y ( z ) + c 42 Y 2 ( z ) + c 43 Y 3 ( z ) ■

После преобразований получаем передаточную функцию, которая по структуре не является канонической:

rr / \ _ Y 4 ⁽ z ) _ c 43 z ⁺ ( c 42 ^C 43 c 21 ) z ⁺ c 41

⁽ z ^{) =} X ( z )⁼ z ² - ( C 32 + C 21 ) z - C 31 . ⁽⁾

Для получения новых канонических структур необходимо приравнять нулю некоторые коэффициенты c_ij так,чтобы в числителе и знаменателе остава-лисьполиномывторогопорядкаобщеговида.Такими коэффициентами могут быть с₂₁ , с₄₂ и с₃₂ .Обнуление с₂₁ приводит к уже известной канонической форме I.

Новая каноническая структура может быть полу-чена,если положить,что с₄₂ = 0.Передаточная функция примет вид:

H ( z ) = ^c 43 ^{z - c} 43 ^c 2i ^z + ^c 4i z 2 ^- ( c 32 ⁺ c 21 ) z ^- c 31

Соответствующая структурная схема представлена на рис. 4.

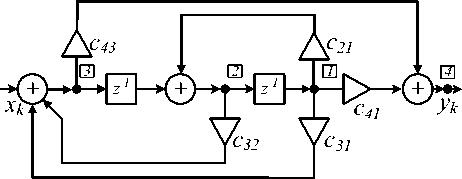
Рис. 4. Каноническая структура при c ₄₂ = 0

Приравнивая коэффициенты при одинаковых степенях z в соотношениях (1) и (12), получим:

c43   a0 ’ c21 = -a1 /a0 ,

* c 41 = a 2 ^, c 32 = ^b 1 ⁺ a l l^a0 ^, _ c 31 = ^b 2 .

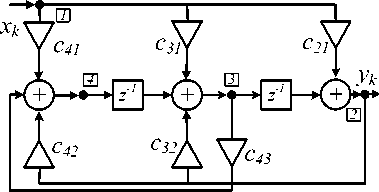
Рис. 6. Обобщенная структурная схема, соответствующая топологической матрице (13)

Аналогично, полагая в соотношении (10) c₃₂ = 0, получим передаточную функцию

Из системы уравнений, описывающих работу схемы (см. рис. 6):

H ( z■ ) =

2 ^c 43 ^z

+ ( c42

— c43c21 ) z +

^c 41

z — C21 z — C 31

Y ( z ) = X ( z ) ,

Y 2 ( z ) = C 2 Y 1 ( z ) + Y 3 ( z ) z",

Y 3 ( z ) = c 31 ^Y 1 ( z ) ⁺ c 32 Y 2 ( z ) ⁺ Y 4 ( z ) z - 1 .

которой соответствует структурная схема на рис. 5.

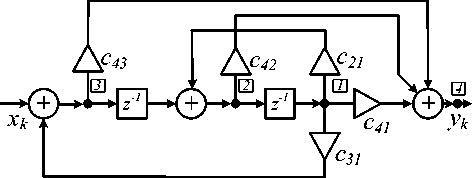
Рис. 5. Каноническая структура при c ₃₂ = 0

^Y 4 ( z ) = ^C 41 ^Y 1 ( z ) ^{+ C} 42 ^Y 2 ( z ) ^{+ C} 43 ^Y 3 ( z ) ’

получаем передаточную функцию

Коэффициенты фильтра связаны в данном случае с коэффициентами передаточной функции (1) следующими равенствами:

H ( z ) = Y 2 ⁽ z ) = c 21 z ^{2 +} ( c 31 - c 43 c 21 ) z ⁺ c 41

X ( z )      z 2 - ⁽ c 32 ⁺ c 43 ) z - c 42

При с₄₃ = 0 получаем известную каноническую структуру II.

Для получения новых канонических структур можно, во-первых, положить c ₃₁ = 0. Полученная структурная схема приведена на рис. 7.

c 43 = a 0 ’ c 42 = a l ⁺ a 0 ^b 1 ^,

* c 41 = a 2 , c 32 = ^b 1 ⁺ a l /a 0 ’ c 31 = ^b 2 .

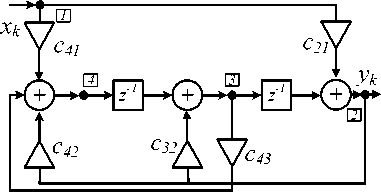
Рис. 7. Каноническая структура при c ₃₁ = 0

Синтез новых канонических форм на основе канонической формы II

Для схемы с элементами задержки, расположенными как в канонической форме II, топологическая матрица T в общем случае имеет вид:

	⎡0	0	0	0⎤
.^^ T=	⎢c 21 ⎢c 31	0 c 32	-1 z 0	0⎥⎥ z -1 ⎥	,          (11)
	⎣c 41	c 42	c 43	0⎥⎦

(для схемы, представленной на рис. 2, с₄₃ = 0). Соответствующая неканоническая структурная схема приведена на рис. 6.

Соответствующие формулы для вычисления коэффициентов ЦФ (см. рис. 7) по коэффициентам передаточной функции (1) имеют следующий вид:

c21   a0, c43 ~ - al I a0 ,

* c 41 = a 2 ^, c 32 = ^b 1 ⁺ a l J ^a0 ’ c 42 = ^b 2 ■

Еще одну каноническую структуру можно получить, если принять с₃₂ = 0. Передаточная функция в этом случае имеет вид:

H ( z ) =

c 21 z ² + (C„ - = 43 = 21 ) z + ^C 41

z

c 43 z - c 42

Новая каноническая структура и система равенств, связывающих данную структуру с передаточной функцией (1), приведены на рис. 8 и в соотношениях (12).

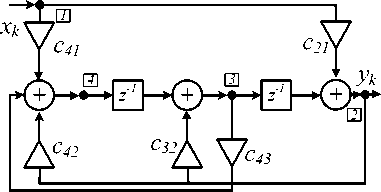
Рис. 8. Каноническая структура при c32 = 0

c21 = a0 ’ c31 = al + aobi,

' c41 = a2 , c43 = b1, c42 = b2 ■

Выводы

Получены четыре новые канонические структуры рекурсивных ЦФ второго порядка. Новые структурные схемы позволяют увеличить число альтернатив при практической реализации ЦФ. Предложенную методику можно расширить для ЦФ второго порядка, структурные схемы которых обладают большим числом узлов, а также применить для получения канонических структур рекурсивных ЦФ более высоких порядков.