Синтез одноканальной системы разгрузки кинетического момента инерционных исполнительных органов космического аппарата

Автор: Зубов Николай Евгеньевич, Микрин Евгений Анатольевич, Негодяев Сергей Серафимович, Рябченко Владимир Николаевич

Журнал: Труды Московского физико-технического института @trudy-mipt

Рубрика: Геокосмическая механика и энергетика

Статья в выпуске: 3 (15) т.4, 2012 года.

Бесплатный доступ

Рассматривается задача гравитационной разгрузки кинетического момента инер- ционных исполнительных органов космического аппарата в канале тангажа для кру- говых и эллиптических орбит с использованием ленточного критерия управляемости. Синтезированы законы управления гравитационной разгрузки и стабилизации заданно- го положения космического аппарата, однозначно определяемые параметрами объекта и задаваемыми коэффициентами характеристического уравнения.

Инерционные исполнительные органы, разгрузка кинетическо- го момента, обратная связь по состоянию, замкнутая система, ленточный критерий управляемости, ортогональный делитель нуля

Короткий адрес: https://sciup.org/142185848

IDR: 142185848

Текст научной статьи Синтез одноканальной системы разгрузки кинетического момента инерционных исполнительных органов космического аппарата

Использование инерционных исполнительных органов (ИИО) в контурах управления ориентацией космического аппарата (КА) позволяет на порядок повысить точность ориентации [1].

Принцип функционирования ИИО основан на. обмене кинетическим моментом между корпусом КА и системой ИИО. Под действием моментов внешних сил КА приобретает угловую скорость и, следовательно, кинетический момент. Далее, за. счет управления кинетический момент КА передается с корпуса. КА на. систему ИИО, и угловая скорость КА обнуляется [1]. Таким образом, ИИО является «интегратором» моментов внешних сил, действующих на. КА. Если момент внешних сил имеет постоянную составляющую, то происходит накопление кинетического момента, системы ИИО и, как следствие, ее насыщение. При достижении предельной величины располагаемого запаса, кинетического момента, системы ИИО необходимо провести сброс (разгрузку) накопленного кинетического момента.

Реализовать разгрузку можно путем включения реактивных двигателей [1]. Однако при этом расходуется топливо. Безрасходный сброс накопленного кинетического момента, в частности, можно осуществить с использованием момента, гравитационных сил. В этом случае разгрузка реализуется путем задания определенного углового движения КА относительно гравитационного поля Земли на участках полета, свободных от решения целевой задачи. Метод управления угловым движением при одновременном регулировании накапливаемого на. ИИО кинетического момента, позволяет сделать гравитационную разгрузку полностью автономной за. счет небольших угловых отклонений от положения равновесной ориентации, рассчитываемых в контуре управления, с целью создания разгружающего гравитационного момента.

Исследованию такого управления КА в канале тангажа для круговых и эллиптических орбит с использованием ленточного критерия управляемости при реализации модального подхода, и посвящена, данная статья.

Линеаризованные уравнения углового движения КА с ИИО для канала, тангажа, в случае круговых орбит при учете действия гравитационного момента, в соответствии с [2] имеют вид

^ = 3^^J - ^J^ ₊ и . - Н ^ . ₍₁₎

^J Z ^J Z ^J z

Применительно к задаче разгрузки кинетического момента уравнения (1) можно записать так:

Р = 3_Ш2 (^J'./') cos(29g)P + 2 w2 J¹^^ sin(29o) - ^, h_г = U z , (2)

здесь J_x,J y ,J_Z — главные центральные моменты инерции КА, wo — орбитальная угловая скорость движения для круговой орбиты, H_Z — кинетический момент ИИО в канале тангажа, u _z — управляющий момент в канале тангажа, Р — малый угол отклонения от углового положения (0, 0, 9д) в канале тангажа. Р = 9 — 9д.

Соответственно для эллиптических орбит уравнения (2) будут иметь вид [3]

р = 3 g ( 4^) cos(29o)P + 2 £ ( '.') sin(29o) — 2£ е .- — ^,h z = U z . (3)

Управляющее воздействие u _z будем формировать в виде линейной комбинации:

U z

^— ^K z 1 ^P ^—

^K z 2 ^p ^{+ K} z 3^h z ⁺ ^K z 4

J hZdt.

В дальнейшем в силу большей общности уравнений для эллиптических орбит рассмотрим именно их.

При переходе к описанию в пространстве состояний уравнения (3) и (4) будут иметь следующий вид:

Х 1	- =	■ 0	1	0	0"	Х 1	-_{- +}	■₀ 1 - J zz 1	U z =	■ 0 "
Х 2		°21	0	0	0	Х 2				S^(t)
Хз		0	0	0	0	Х з				0
_ Х4.		0	0	1	0_	_ Х4_		0		0

U z

—k^T x = [ K z 1 I K z 2

| ^— ^K z 3

\ ^— ^K z 4 ]

Х 1

Х 2

Х3

_ Х4_ где

G \ _TOs(29o), _S(t) = ³ G ^J Jy -_ Jyy sin(29o) — 2^Gesin^,

T³ J zz 2 T ³ J zz ) T ³

kT — вектор коэффициентов регулятора, а вектор состояния имеет компоненты

x = [х1 | Х2

I Хз | Х 4] = р

9 h z

t ^Т

J h_Z dt .

Динамическая система. (5) является нестационарной с медленно меняющимися периодическими коэффициентами. Для применения математического аппарата стационарных систем аппроксимируем коэффициент 021 кусочно-постоянной функцией вида

°21 = ^3^{(1(t — tj)}°2i ^{— 1(t —} ^+1 ⁾⁾ ^о 2р г =1

Примем для г = 1 момент времени прохождения перигея t. В этом случае система (5) становится стационарной.

2. Ленточный критерий управляемости и его применение для синтеза управления

Найдем решение задачи разгрузки на основе ленточного критерия управляемости, описанного в [4, 5].

Рассмотрим динамическую систему в виде пари матриц с постоянными коэффициентами:

(Ab),(7)

где A G R^nxn, b G Rⁿ, R^p — р-мерное вещественное пространство. Другими словами, пара (7) описывает систему

X(t) = Ax(t) + bn(t).

Пусть характеристический полином матрицы A имеет вид det(AIn — A) = An + «п-1Ап-1 + • • • + «1А + «о A G C,(9)

где i_n — единичная матрица размера пхп, C — комплексная плоскость. Пусть также 01_Хп — нулевая строка размера 1 х п, тогда динамическая система (7), (8) полностью управляема, если ленточная матрица управляемости [4]

"—ьМ 0 0 ••• 0⎤ bL —Ь^А 0 ••• 0 ⎢0 bL —Ь^А ••• 0 Г°1хп0к± . = l in г к ' ■ 0 (Ь^А) _ 01хп_| ⎢⎢ 0 0 ь • • • • • • • • • • • • • • • • • • —ь£ А 0 0 0 • • • ь^ имеет полный ранг по строкам.

Здесь 0 — символ операции кронекерова произведения, например,

	° 11А1	⁰ 1Д12	⁰ 11Дз	⁰ 12 Ь 11	⁰ 12 ^ 12	° 12 Ь 13"
	0 11 ^ 21	0 11 ^ 22	0 11 ^ 23	0 12 ^ 21	0 12 ^ 22	0 12 ^ 23
г -\| ^ 11 ^у 12 0 13 ^{011 012} L к к	⁰ 1Дз1	° 1Дз2	⁰ 11 Ь зз	⁰ 12 ^ 31	⁰ 12 ^ 32	⁰ 12 ^ 33
⁰ ° 21 ° 22 ° 23 = L⁰²¹ ^О221	⁰ 21А1	⁰ 21 ^ 12	⁰ 21 Ь 13	⁰ 22 ^ 11	⁰ 22 ^ 12	⁰ 22 ^ 13
L° 31 ° 32 O 33J	0 21 ^ 21	⁰ 21 ^ 22	⁰ 21 Ь 23	⁰ 22 ^ 21	⁰ 22 ^ 22	⁰ 22 ^ 23
	. ⁰ 21 ^ 31	⁰ 21 ^ 32	⁰ 211>33	⁰ 22 ^ 31	⁰ 22 ^ 32	⁰ 22 ^ 33_

Символом Ь р G R^{(n 1)хп} обозначена матрица — левый делитель нуля (аннулятор) ранга п — 1, т.е.

^b L = ⁰ ( п - 1) х 1 .

Заметим, что далее по тексту символом Х^ будет обозначаться [5] левый делитель нуля (аннулятор) матрицы X максимального ранга, Х^ — правый делитель нуля (аннулятор) матрицы X максимального ранга, Х ⁺ — псевдообратная матрица Мура-Пенроуза.

Для полностью управляемой динамической системы между коэффициентами «г характеристического полинома (9) и ленточной матрицей управляемости

И ^{0 ь} ^ ^— {ог ^т! ^{0 (ЬМ) 1101}

имеется следующая однозначная взаимосвязь:

« о

X 1

« 1

« п — 2

« п - 1

= ( И 0 ь+—И 0 (Ь+А))

п — 1

XT"

Здесь Р = 0 — ненулевой скаляр,

PM ® b + — {гТ^Ц ⁰ ( b +^А) = L I n J [O ixnJ			^⎡- b ⁺ A		0		0		···	0 ^⎤	,
			b ⁺		-b⁺A		0		···	0
			0		b⁺		- b ⁺ A		···	0
			0		0		b ⁺		• • •	• • •
			• • •		• • •		• • •		• • •	-b ⁺ A
			0		0		X1 ⎤	0	• • •	b ⁺
^(︂	0 ixn	- ^{0 b}L	I n	" ^{0 (b}L^A))		• • •		- =0. (11)
	I n		_ 0 ixn_
						^n—i
						L Xn J

Другими словами, для полностью управляемой многомерной системы (и только для нее) решение однородного уравнения (11) является вектором, а не матрицей.

Справедливой оказывается следующая

Теорема [4]. Пусть линейная система (7), (8) полностью управляемая и имеет характеристический полином (9). Тогда регулятор kT в законе обратной связи, обеспечивающий замкнутой системе заданный характеристический полином det (AIn — A + bkT) = An + Pn—iAn 1 + • • • + PiA + Po, определяется формулой

k ^T = AaT^-i

где

Aa = [ao — Po

T = (Xi

| ^ai ^{— p}i | • • • | ^a n - i ^{— p}«-i] , I X 2 ••• I Xn-i I X n )

— матрица Крылова,

№ ^ b * — { o iSn} ^ H

X n - i X ;

X n = b .

Таким образом, согласно формулировке теоремы справедливым оказывается следующее равенство:

det (A I ; — A + b AaT ⁱ) = Aⁿ + Pn—iA^{n i} + • • • + Pi A + Po.

3. Синтез одноканальной системы разгрузки кинетического момента инерционных исполнительных органов КА

В рассматриваемом нами случае модель КА имеет вид

A =

■ 0	1	0	0"
«2i	0	0	0
0	0	0	0
0	0	1	0_

b =

При этом

^⎛ .....г	■₀	1	0	0"	^⎞		AI4 —	■₀	1	0	0"	= A⁴ — a_2iA²
	O2i	0	0	0	I)	=		O2i	0	0	0
	0	0	0	0				0	0	0	0
	0	0	1	0_				0	0	1	0.

Будем предполагать, что замкнутой системе требуется обеспечить гурвицев (устойчи вый) полином:

det(A l 4 - A + b A«T^-1) = А⁴ + РзА³ + Р2А² + Р1А + р о . (14)

Вычисляя матрицу bf, получаем bf

"1	0	0	0"
0	J ..	1	0
0	0	0	1_

Следовательно, ленточная матрица (10) имеет вид

I n 0 1x n

0 (bf A) =

0 1x n I n

0 b f -

= I 0,	"₁	0	0	0"
	0	J ..	1	0
	0	0	0	1_

I 4

⁺ 0 1x4

^J zz °21 0

1 0 0"

0 0 0

0 1 0

11 размеры 15 x 16.

Правый делитель нуля максимального ранга матрицы (15) равен

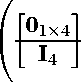
"₁	0	0	0"
0	J ..	1	0
0	0	0	1_

+ foI 4 ⁰

0 1x4

"₀	1	0	0"
^J .. °21	0	0	0
0	0	1	0_

= [0 0 0 -21 I 0| 0| -021 I 0 - 0 0| 0| 1 0 - , 1;

I 1 <

Из (16) следует, что матрица Крылова (13) равна

€ R16.

T = (X1 I X2 \| Хз I b) =	"₀	0	1 --Т---	0 "
	0	0	0	1 --Т---
	0	^- ^о 21	0	1
	.^- ^о 21	0	1	0 .

Подставляя в формулу (12) матрицу (17) и вектор разностей коэффициентов характеристических полиномов

А« = [«о - Ро	« 1 ^- Р1	«2 - Р2	«3 ^{- р}з] ,
получаем формулу регулятора:	k ^T = A«T^-	1=
		"₀	0	1 --7---	0 "	-1
= [«0 ^- Ро « 1 ^- Р1 «2 ^{- р}2	«з ^{- р}з]	0	0	0	1
= [«0 ^- Ро « 1 ^- Р1 «2 ^{- р}2	«з ^{- р}з]	0	^-°21	0	1
		.^-°21	0	1	0 .

= [-Jzz(°21 + Р2) - ^ | -JzzР3 - ^ | -5l | -^2l] , т.е. согласно закону управления (6)

К.1 = Jzz(о21 + р2) + ^Д^ , Kz2 = JzzРз + ^ , к.3 = - i2i, к.4 = - i2i.

Непосредственной подстановкой можно убедиться, что

A - b AaT^-1

0	1	0	0 "
-З₂ - — ^{Р 2} «21	-Зз - — ^{Р 3} « 21	d 1 3-л-л « 21	d o ' -- « 21
^J zz ⁽« 21 ^+З 2 ⁾⁺ « ₂₁	^J zz 3 з + ДУ	« 21	d o « 21
0	0	1	0

а характеристический полином матрицы (19) совпадает с правой частью (14), т.е.

Л	-1	0	0 "
З2 + — ² « 21	^Л + З з + « 21	d 1 ' -- « 21	d o ' -- « 21
^J zz ⁽« 21 ^+З 2 ) « ₂₁	^J zz ^З 3 '« 2 ^ 1	Л - ^1 « 21	d o - « 21
0	0	-1	Л

— А⁴ + З з Л³ + З 2 Л² + З 1 Л + З о .

Это и требовалось получить.

Таким образом, закон управления КА, обеспечивающий разгрузку кинетического момента инерционных исполнительных органов в канале тангажа и обеспечивающий заданные моды колебаний, имеет следующий вид:

- z — (J zz (« 21 + З2) + ^J" ^P + Г/ . . З з + ^J ^zz ³ ¹ P + — K_z + — / K_z dt.

V «21 / \ « 21 / « 21 « 21 J

Как видно из (20), управление однозначно определяется параметрами объекта и задаваемыми коэффициентами характеристического уравнения.

Закон разгрузки (20) может быть преобразован в закон стабилизации. В этом случае будет иметь место редуцированная модель КА:

А = л red ■ 0 1 0" ■ 0 " «21 0 0 , bred 1 - 0 0 0_ 1 и редуцированный закон управления:

^U zred ^— ^J zz ⁽« 21 ^{+ З} 2 ^{)р +} f ^J zz ^З 3 +-- ~^P ⁺ ~~ ^z \ « 21 « 21

с редуцированным регулятором kred — [-Jzz(«21 +32) | -JzzЗ3 - '-Щ | -у^] •

При этом редуцированный полином det(AI3 - Ared + bredkred) — Л3 + З3Л2 + З2Л + З1

априори считается устойчивым.

Дальнейшее упрощение задачи приводит к модели КА второго порядка:

—

А , _ -

■ 0

—

^л red —

, ^ured —

[ «21

' --

и закону управления

где полином

kred — ( — Jzz («21 + З2) | -JzzЗз) , det(AI2 - Ared + bredkred) — Л2 + З3Л + З2

также считается устойчивым.

Действительно, подставляя (21) и (22) в формулу, имеем:

^det( ^AI 2 ^- .А. _те д + b red kre d ) ^—

— det (а Ш —

V [ О 1J |_О21

0- + [ 1 ] [^-^ zz ⁽« 21 + ^ 2 ) |

J zz З з

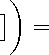
det М 442

~З^ ^ — А^{2 +} /З 3 А ⁺ З 2 .

Что и требовалось получить.

4. Заключение

В работе предложено решение задачи одноканальной гравитационной разгрузки кинетического момента инерционных исполнительных органов КА для круговых и эллиптических орбит. Решение основано на ленточном критерии управляемости многомерной динамической системы.

Полученные законы управления гравитационной разгрузки и стабилизации заданного положения КА однозначно определяются параметрами объекта и задаваемыми коэффициентами характеристического уравнения.

Работа выполнена при финансовой поддержке Правительства Российской Федерации в рамках контракта с Минобрнауки России А'2 13.G25.31.0028.

Список литературы Синтез одноканальной системы разгрузки кинетического момента инерционных исполнительных органов космического аппарата

Теоретические основы проектирования информационно-управляющих систем космических аппаратов//под общей редакцией д.т.н. Е.А. Микрина. -М.: Наука, 2006.
Раушенбах Б. В., Токарь Е. Н. Управление ориентацией космических аппаратов. -М.: Наука, 1974.
Тимаков Н. С. Исследование управляемого углового движения космического аппарата на высокоэллиптической орбите//Навигация и управление движением. Материалы IX конференции молодых ученых. -СПб. -2007. -С. 330-336.
Мисриханов М. Ш., Рябченко В. Н. Ленточная формула решения задачи А.Н. Крылова//Автоматика и Телемеханика. -2007. -№ 12. -С. 53-69.
Мисриханов М. Ш., Рябченко В. Н. Алгебраические и матричные методы в теории линейных MIMO-систем//Вестник ИГЭУ. -2005. -Вып. 5. -С. 196-240.

Статья научная