Синтез одноразрядного помехоустойчивого умножителя

Теория многомерных цифро-векторных множеств [1] - новый универсальный метод синтеза комбинационных схем, в основу которого положена классическая теория множеств, где нумерованное множество чисел расширенного ряда располагается в ячейках физического пространства, идея построения которого предложена в XIX в. русским ученым Е. С. Федоровым. При таком синтезе главным является построение многомерных таблиц истинности и на их основе - геометрических образов исправленных логических или арифметических функций, а схемное выполнение конкретного цифрового устройства, реализующего эти функции, может быть полностью автоматизировано с помощью вычислительной техники.

Одной из первоочередных задач, которую нужно решить при проектировании цифровых систем электроприводов и приборов энергоснабжения авиационно-космических комплексов является исправление ошибок, вызываемых внутренними и внешними помехами, а также резервированием функциональных узлов и системы в целом. Метод многомерных цифро-векторных множеств [2] позволяет решить эту сложную задачу.

Исправление любых ошибок определяется покрытием определенных совершенных геометрических образов выходных сигналов устройства умножения. Эти геометрические образы, представляющие собой комбинационные схемы с двух- или многоуровневым принципом реализации, могут быть как в неизбыточных кодах (двоичных, нетрадиционных двоичных, например коде Грея [3]), так и в избыточных, например многофазных и интегральных. Причем наглядный геометрический образ любых логических и цифровых функций с помощью покрытий определяет все возможные варианты выполнения принципиальных схем. Предложенный метод [4] не имеет ограничений на параметры реализуемых функций.

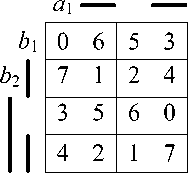
Рассмотрим пример синтеза одноразрядного устройства умножения, допускающие без нарушения их работы одиночные ошибки во входных сигналах операндов оснований систем счисления n = 4. Для решения данной задачи применяется синтезированный систематический код, где информационные разряды (входы умножителя) коды A ( a i , a 2 ), B ( b 1 , b 2 ) связаны с эквивалентными цифрами контрольной части кода X ( X 1 , X 2 , X 3 ) , общими для этих двух операндов, зависимостью, приведенной на рис. 1.

Далее используются следующие условные обозначения: латинская цифра с индексом цифрой обозначает фигуры размером 4x4, пронумерованные построчно сверху вниз. Индекс идентифицирует геометрический образ исправленного сигнала; подчеркивание символа снизу обозначает инверсию сигнала.

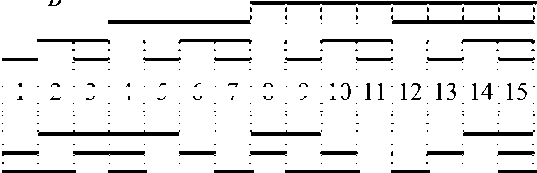
Связь между информационными сигналами операндов и выходными сигналами умножителя определяется четырьмя геометрическими образами (рис. 2).

a 2-------

А

X

0123456789 10

Рис. 1. Зависимость информационных сигналов с контрольной частью

0 1 2 3

0	0	0	0
0	1	2	3
0	2	10	12
0	3	12	21

		*	*
	*		*
	*	*

		*	*
		*

			*

Рис. 2. Геометрические образы выходных сигналов умножителя

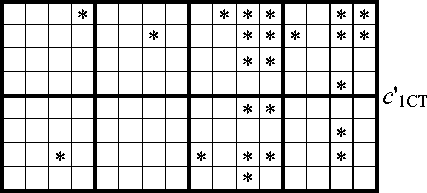
На рис. 2 видно, что выходные сигналы сумматора являются множествами цифр основания системы счисления n = 16: c 1МЛ = 5 V 7 V 13 V 15 , с 2мл = 6 v 7 v 9 v 11 v 13 v 14, c 1ct = 10 v 11 v 14, c 2_CT = 15 .

Распределение эквивалентных цифр (0 - 15) информационной части кода и этих же цифр при одиночных ошибках в информационных и контрольных разрядах кода определяется рис. 3.

b 2 _______________________

AB      b 1

a -2____ ________ ________ ________ a 1

0 1 2 3 4 5 67 8 9 10 11 12 13 14 15

X 1 0 X 2     | 1 X 3 1 Р 4 , 1 5 1 1 7	0	0	0	11	0	5	6	7	0	11	11	11	12	13	14	11
	0	5	2	3	5	5	14	5	8	9	14	11	14	5	14	14
	0	1	6	3	6	13	6	6	8	13	10	11	13	13	6	13
	8	3	3	3	4	5	6	3	8	8	8	3	8	13	14	15
	0	1	2	7	12	7	7	7	12	9	10	11	12	12	12	7
	2	9	2	2	4	5	2	7	9	9	2	9	12	9	14	15
	1	1	10	1	4	1	6	7	10	1	10	10	12	13	10	15
	4	1	2	3	4	4	4	15	8	9	10	15	4	15	15	15

Рис. 3. Одиночные ошибки в ячейках пространства

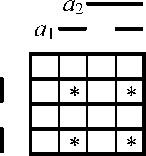
Отсюда нетрудно представить геометрические образы результата умножения с исправлением ошибок входных сигналов (рис. 4).

b 2

X

x - 3

^x 1 0

^x 2 | 1

I 7

AB b 1

a 2 “ a 1-----

0 1 2 3 4 5 6 7 8 9 101112131415

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

* *

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

* *

*

*

*

*

*

*

*

b 1 b 2 x 3

c '1МЛ

1 1	2 1	3 1	4 1
5 1	6 1	7 1	8 1

b 1 b 2 x - 3

^c 2МЛ

1 2

2 2

8 2

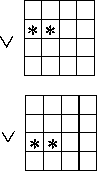
b 1 b 2 x " 3

3 3

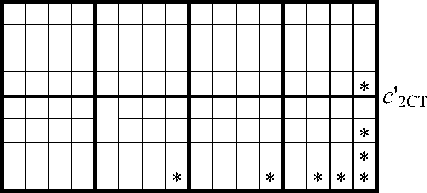
Рис. 4. Геометрические образы исправленных сигналов

b 1 b 2 x 3

0	0	0	7 1
0	7 1	7 1	1 4

Покрытие цифровых множеств этих геометрических образов в пространстве координат AB(a 1, a2, b 1, b2) X(x 1, x2, x3) либо координат b 1 b2x3 определяет логическую функцию, исправляющую все одиночные ошибки. С учетом этого логические выражения исправленных сигналов можно записать в виде с'1МЛ = 11 b 1 b2x3 v2 1 b 1 b2x3 v3 1 b 1 b2xs v4 1 b 1 b2x3 v5 1 b 1 b2x3 v6 1 b 1 b2x3 v7 1 b 1 b2x3 v8 1 b 1 b2x3, с‘2мл = 12b 1 b2x3 v22 b 1 b2x3 v32b 1 b2x3 v42b 1 b2x3 v52b 1 b2x3 v62 b 1 b2x3 v72_b 1 b2x3 v82 b 1 b2x3, с'1ст= 51 b 1 b2 x3 v 13 b 1 b2 x3v23_b 1 b2 x3v33 b 1 b2x3v43_b 1 b2x3 v53_b 1 b2x3 v63 b 1 b2x3, с‘2ст= 71 b 1 b2x3 v71 b 1 b2x3 v71 b 1 b2x3 v 14 b 1 b2x3.

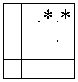
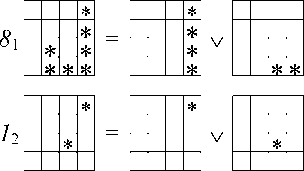
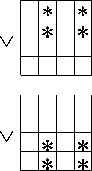
Здесь подмножества ( 1 1 - 8 1 ), ( 1 2 - 8 2 ), ( 1 3 — 6 3 ), 1 4 определяются по следующим зависимостям:

*

= а । а ₂ х । Х 2

*

*

*

*

*

*

*

*

*

*

*

v

*

*

*

*

*

*

*

*

*

*

*

*

*

v

*

*

*

*

*

*

= а 1 а ₂ v а 1 х ₂ v а ₂ х 1 х ₂ ,

= а । а ₂ х । х ₂

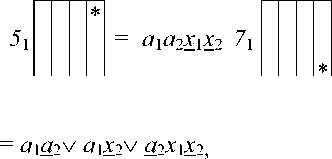
а 1 а 2 х 1 х 2 ,

*

*

*

*

ж

*

v

* ж ж ж

*

= а 1 а ₂ v а ₂ х 1 х ₂ v а 1 х ₂ ,

= а 1 а ₂ v а ₂ х 1 х ₂ v а 1 х ₂ ,

5 1 v 4 3

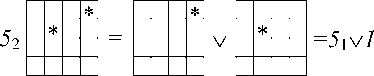
1 ,

*

*

*

*

*

*

*

*

*

*

*

v

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

v

v

*

*

*

*

*

*

*

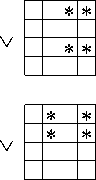
х 1 х2v а 1 а2v а 1 а2х 1, x2a2v а 1 x1v а 1 х2,

v

*

*

*

*

v

v

v

*

*

x2 a 2v х 1 х 2v а 1 а 2v а 1 x 1 х2 v а 1 a2х 1v а 1 a2х2,

= x 1 a ₂ v а 1 x 1 х ₂ v а 1 a ₂ х ₂ ,

= x ₂ a 1 v а ₂ x 1 х ₂ v а 1 а ₂ х 1 ,

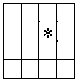
= а 1 а 2 х 1 х 2

= 1 3 v 4 3 ,

	*	*	*
		*	*
		*	*

		*	*
		*	*

		*	*
*		*	*
		*

		*	*
		*	*

		*	*
*		*	*
		*

		*	*
		*	*

		*	*
		*	*

		*
		*

		*
		*

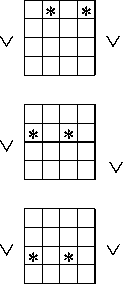
a ₂ x ₂ v a 1 x 1 x ₂ v a ₂ x 1 ,

a ₂ x ₂ v a 1 x 1 x ₂ v a 1 a ₂ x 1 ,

x 1 a ₂ v a 1 x 1 x ₂ v a 1 a ₂ x ₂ ,

= a 1 a ₂ x 1 v a 1 x 1 x ₂ v a ₂ x 1 x ₂ v a 1 a ₂ x ₂.

Подставляя значения логических выражений всех подмножеств в выражения для сигналов С ' _1мл , С ' _2мл , С' ict , С '_2СТ , получаем запись, определяющую конструкцию схемы исправления ошибок.

В рассмотренном варианте исправления ошибок используется алгоритм многоуровневого синтеза, когда покрытие геометрических образов начинается с рассмотрения подмножеств в младших ячейках цифрового пространства с последовательным переходом к его старшим ячейкам. Такой вариант алгоритма синтеза позволяет минимизировать аппаратурные затраты за счет определенного снижения скорости выполнения операции.

Заключение. На базе теории многомерных цифро-векторных множеств синтезирован одноразрядный помехоустойчивый умножитель, используемый в любых системах цифровой обработки сигналов, где необходимо обеспечить бесперебойную работу и высокую надежность цифровых и логических схем. Данный синтез применим для любых оснований систем счисления и способов кодирования цифровых данных. Продемонстрированы универсальность и наглядность данного метода.