Синтез оптической антенны

СИНТЕЗ ОПТИЧЕСКОЙ АНТЕННЫ

Теория синтеза антенн в радио и СВЧ диапазоне детально разработана и обобщена в ряде монографий [1,2]. Назовем оптической антенной устройство для излучения и приема электромагнитных волн оптического диапазона, обеспечивающее требуемые характеристики направленности и позволяющее решать задачи локационной и навигационной техники. В работе [з] сделана попытка формально перенести теорию радиоантенн в оптический диапазон. Однако оптические антенны обладают рядом особенностей:

• 1)    наиболее интересная область действия оптической антенны относится к зоне френелевской дифракции, являющейся лишь переходной зоной для радиоантенн;

• 2)    поле в раскрыве антенны, вообще говоря, не является строго монохроматическим и пространственно когерентным, причем разрешение по углу в оптической антенне связано со степенью пространственной когерентности источника излучения;

• 3)    классические оптические элементы типа линз, зеркал, диафрагм дают лишь ограниченные возможности варьирования поля в раскрыве с целью получения нужной диаграммы направленности в отличие от произвольно управляемых антенных решеток, применяемых в радиоантеннах.

В данной работе вводится понятие диаграммы направленности в зоне френелевой дифракции для излучения с произвольной степенью когерентности. Для формирования требуемого поля в раскрыве предлагается использовать искусственные оптические элементы, синтезируемые с помощью ЭВМ [4].

Пусть плоский раскрыв Л оптической антенны содержит оптический элемент Л с функцией комплексного пропускания T(u, v) (на заданной частоте v), освещаемый протяженным источником света о (рис. 1).Вначале предположим, что источник о является строго монохроматическим с длиной волны X = ^ и создает в плоскости раскрыва (и, v) = и освещающее поле с комплексной амплитудой Е(и). Комплексная амплитуда поля в точке наблюдения (х, у, z) = (х, z) связана с полем в раскрыве (1)

W(u) = Е (и) • T(u, v)(1)

интегралом Кирхгофа

.    1 , exp(ikL) z ,—...

w(x, z) = jy / W(u) —---- jjdu,(2)

Д

Рис. 1. Геометрия оптической антенны

где

L = Их-u)2 + z2 к = ^ .                                      (3)

Представим излучение антенны исходящим из некоторой мнимой точки С (см. рис. 1), называемой фазовым центром:

w(x~ z) = Е_о ^Е^-^¹ D(5), Е_о = const,                           (4)

где R - расстояние от фазового центра до точки наблюдения;

• ^ - угловая координата точки наблюдения, отсчитанная из фазового центра антенны.

Если f0 - расстояние от фазового центра до плоскости раскрыва, то в равенстве (4):

• 5 =    , R = /х2 + R2 , R = fo + Z.(5)

R             ’          ZZ

Z

Соответственно введем "приведенное поле в раскрыве" W^(и)согласно уравнению

W(u) = Ео —p(f-kf} Wn(u), f = ^u2 + fo.(6)

Для упрощения преобразований рассмотрим параксиальное приближение

~ « 1, UCA, -1|1 « 1.(7)

Подставляя равенства (4) и (6) в уравнение (2) , получаем

D(^ = iTf~ ; V^ ехр[т^ <и - fo Л П Л1

5) 2 du,

где ffi - приведенное расстояние.

Равенства (4), (6) позволяют "выделить" из наблюдаемого поля w точечный источник, расположенный в фазовом центре С. Функция D(0) (8) определяет угловое распределение комплексной амплитуды излучения точеч- ► ного источника. Будем называть функцию 0(0) диаграммой направленности оптической антенны. Уравнение (8) показывает, что диаграмма направленности связана с приведенным полем в раскрыве оптической антенны преобразования Френеля, в то время как в радиоантеннах фигурирует двумерное преобразование Фурье [1]. Кроме того, здесь имеется слабая зависимость О от расстояния z, исчезающая при z » f₀.

Обобщим полученные соотношения на случай полихроматического протяженного освещающего источника о. Регистрируемая фотоприемными приборами величина интенсивности излучения оптической антенны в случае частично-когерентного света, как известно [5], выражается через взаимные функции когерентности. Введем взаимную функцию когерентности Гн (x-t, z, ,х2 , z2 , т) наблюдаемого поля оптической антенны, взаимную функцию когерентности поля, освещающего раскрыв r0(ui,u2,r), а также соответствующие им взаимные спектральные плотности [5]

GH(xi, z1z х2, z2, у) и Go(un, u2, v).

По аналогии с (4) произведем разделение зависимости от угловых координат 0 и расстояния R от точки наблюдения до фазового центра ан тенны :

Г (x1f z1z х2, z2, т) = |ЕоГ gxpjik(R1-R2)] Q (© © т) (10)

• Н                                       Ri R2

0ц =       . R =                j = Т72, k = ^(ii)

J X О j                  J          Jс

В частности,

1(х, z) = IЕоI2 ^ q(Q).

Функцию

0(0) = 0н(0, 5, 0)(13)

назовем частично-когерентной диаграммой направленности (по интенсивности) . Она определяет угловое распределение интенсивности излучения оптической антенны в частично-когерентном свете.

Введем "приведенную" взаимную спектральную плотность G^fu-i, u2, v) из соотношения, аналогичного (6) :

T(ui, v) • Go (u-,, u2, v) • T*(u2, v) = exp[ik (fi -f 2)]

IE"'2 ——.—

^(Ui, u2, v) .

fj. /35 * ^, j = n                                      ns,

(* - символ комплексного сопряжения).

Пользуясь формулой распространения взаимной функции когерентности [5], нетрудно получить для частично-когерентной диаграммы направленности в параксиальном приближении следующее уравнение:

0(0) ⁼ „2 f2 V V dv f f G (U1, u₂, v) • ^{C f}n ⁰ Л Л ^П

exp ■

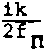
- fo(0)3 -

(u2 - f2(0)3 ’

d u1rdu2

В частности, для квазимонохроматического света со средней частотой v можно рассматривать распространение непосредственно взаимной интенсивности rn(u1f u2, 0) . Можно показать, что в предельном случае полностью когерентного света формула (14) сводится к формуле (6) , а уравнение (16) принимает вид

0(0) = |D(0)I3,                                                           (17)

где

0(0) - диаграмма направленности по комплексной амплитуде (8).

Особый интерес представляет рассмотрение оптических антенных реше ток в виде синтезируемых оптических элементов [4] . Для них

T(u, v)

2          Т У (и) ;

,    . - т пт Лпт

(п,т)е I

и ел,

где

Тпт xnm(^

Обычно

• - коэффициент комплексного пропускания в центре Е^ элемента Л^ антенной решетки;

форма функции комплексного пропускания элемента Л .

V

Лпш

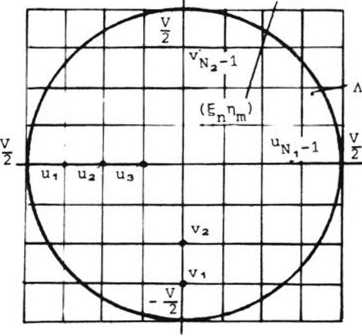
Рис. 2. Геометрия оптической антенной решетки

Q(0) =             Е             Е Т m • с fn (ni,m1) е IN (n2,m2) €IN 11

па т2

где

к

2тту с

Y          (0) = тъ°■2 f / Го (Е + £i,E + nimin2m2       lEol2 д(0) Л(о> гит, 1,ьп2т2

е₂ ,0)

En тfo© expfik (—-—) - ?— Z1

Е- _f

(^^ - —) е2 } dEl d z        rn

е2 .

Задача синтеза оптической антенны ставится следующим образом. За дается взаимная функция когерентности или спектральная плотность поля источника излучения и требуемая диаграмма направленности по интенсивности Qo (0). Требуется подобрать характеристику оптического элемента в раскрыве T(u, у) так, чтобы имела место аппроксимация

Q(^) = Со(0).                                                         (2

Алгоритм синтеза оптической антенны состоит, таким образом, из этапов вычисления взаимной функции когерентности Г_о и решения аппроксимационной задачи (21), где Q(0) задается одним из соотношений: (8),

• (16) или (19) .

Решение аппроксимационной задачи может осуществляться хорошо разработанными численными методами чебышевского приближения комплексных функций. Следует, однако, иметь в виду, что в силу малости длины волны оптические антенные решетки имеют значительное число элементов ~106-108. При расчетах требуется использование мощных ЭВМ.

С использованием разработанных методов и алгоритмов синтезирована на ЭВМ амплитудная маска плоского оптического элемента, формирующая несколько лепестков по одной из угловых координат.