Синтез оптимального алгоритма распознавания типового состава групповой воздушной цели из класса «самолеты с турбореактивными двигателями» на основе калмановской фильтрации и нейронной сети

В [1] предложена концепция всестороннего распознавания воздушных целей (ВЦ) в радиолокационном (РЛ) комплексе воздушного базирования, где центральное место занимает перечень решений летчика и вопросы наведения ракет на ВЦ, основанные на их распознавании. Так, согласно данной концепции, распознавание типового состава групповой воздушной цели (ГВЦ) позволит поддержать следующие решения летчика в воздушном бою:

• –    оценить тактическое назначение группы самолетов противника, степень ее угрозы и возможности по противодействию;

• –    выбрать эффективный тактический прием исходя из особенностей работы бортовых радиолокационных станций (БРЛС) самолетов противника и оружия на их борту;

• –    определить приоритетность воздействия по наиболее опасным целям в зависимости от ситуации и важности целей;

• –    определить очередность обстрела целей;

• –    определить потребный наряд ракет для поражения каждого типа цели в группе;

• –    контролировать типовой состав самолетов группы противника при пуске по ним ракет, а также осуществить оптимизацию наведения управляемых ракет [2-4] :

• – осуществить предстартовое целеуказание (ЦУ) радиолокационной головке самонаведения (РГС) ракеты о типе атакуемой ею целью из состава группы (для оптимизации наведения ракеты на заданный тип цели из состава группы);

  – осуществить радиокоррекцию в РГС ракеты при ее перенацеливании на другой тип цели из состава группы.

В [5-9] приведены результаты летно-экспериментальных исследований по оценке возможностей распознавания типового состава ГВЦ из класса «самолеты с турбореактивными двигателями (ТРД)» в импульсно-доплеровской БРЛС истребителя. Так, экспериментальным путем установлено, что типовой состав ГВЦ из класса «самолеты с ТРД» принципиально можно распознать на основе анализа взаимного частотного разноса траекторий доплеровских частот РЛ-сигналов, отраженных от планеров самолетов группы и вращающихся лопаток рабочих колес первых ступеней компрессоров низкого давления (КНД) их силовых установок, по которым определяются типы двигателей самолетов группы, а по ним непосредственно и тип каждого самолета в группе.

Полученные при анализе результатов летно-экспериментальных исследований численные значения траекторных статистических характеристик реальных траекторий доплеровских частот были использованы в качестве экспериментальных исходных данных при синтезе и разработке методов и алгоритмов распознавания типового состава ГВЦ, приведенных в работах [10–16].

Их сущность заключается в том, что в амплитудно-частотном спектре РЛ-сигнала, отраженного от ГВЦ, выделяются отсчеты доплеровских частот, обусловленные отражениями сигнала от планеров самолетов группы и вращающихся лопаток первых ступеней рабочих колес КНД их силовых установок. На основе калмановской фильтрации находятся оценки данных отсчетов доплеровских частот, а затем величины их разносов. Принятие решения о типе самолета с ТРД в их группе осуществляется путем попадания разности оценок планерной и компрессорной доплеровских частот в один из априорно сформированных диапазов возможных значений оценок разностей траекторий доплеровских частот. При этом границы каждого поддиапазона определяются выражениями:

^ - W;,                                  (1)

F_B^F_PKN„                                          (2)

где F _Рq – максимальная частота вращения ротора КНД силовой установки q- го типа самолета с ТРД;

b i и b ₂ - соответственно минимальное и максимальное значения величины относительных оборотов вращения ротора силовой установки, одинаковые для всех типов самолетов группы;

N _л – количество лопаток рабочего колеса первой ступени КНД.

Диапазон, в который величина разноса доплеровских частот за определенное время попадает с максимально вероятностью, и будет соответствовать оценке типа самолета с ТРД, находящимся в составе их группы.

Недостатком такого подхода распознавания типового состава ГВЦ из класса «самолеты с ТРД» является непостоянство вероятности распознавания типа каждого самолета с ТРД в их группе. Это обусловлено тем, что решающее правило при распознавании типового состава ГВЦ, во-первых, является неоптимальным, во-вторых, не адаптируется к условиям полета ГВЦ, поскольку оно основано на априорно фиксированных границах сформированных поддиапазонов, определяемых выражениями (1) и (2), в-третьих, необходимо выполнение условия, когда минимальное и максимальное значения величины относительных оборотов вращения ротора силовой установки (b1 и b2, соответственно, в формулах (1) и (2)) должны быть одинаковыми для всех типов самолетов группы.

В действительности же данные априорно сформированные границы каждого поддиапазона в процессе полета ГВЦ могут меняться в зависимости от характера полета самолетов группы, например, с изменением высоты полета или при различных интервалах и дистанциях между самолетами группы при выдерживании заданных параметров боевого порядка в различных его формах («пеленг», «фронт», «клин» и т.д.), когда величины относительных оборотов b 1 и b ₂ вращения ротора силовой установки не будут соответствовать априорно заданным и неравным для всех типов самолетов группы. Поэтому границы поддиапазонов не будут соответствовать априорным их значениям, что в результате приведет к неверному распознаванию типового состава ГВЦ в целом.

В последнее время все чаще и чаще находят применение нейронные сети в различных областях знаний, в том числе и в теории распознавания образов. В этой связи известно [17–19], что нейронная сеть по своим характеристикам эквивалентна оптимальному разомкнутому калмановскому фильтру. Поэтому если предварительно осуществить обучение нейронной сети (решающего правила) изменяющимися во времени разносами доплеровских частот, характерных для каждого типа самолета с ТРД в группе при различном характере его полета, то можно адаптировать оптимальное решающее правило к условиям полета ГВЦ, то есть обеспечить постоянство вероятности распознавания каждого типа самолета с ТРД в группе.

Цель статьи – синтезировать оптимальный алгоритм распознавания типового состава ГВЦ из класса «самолеты с ТРД» на основе калмановской фильтрации и нейронной сети, получить его характеристики с учетом экспериментальных исходных данных по траекторным статистическим характеристикам реальных РЛ-сигналов.

Структура оптимального алгоритма

Оптимальный алгоритм распознавания типового состава ГВЦ из класса «самолеты с ТРД» на основе калмановской фильтрации и нейронной сети состоит из четырех процедур:

процедура получения оценок разносов доплеровских частот на основе калмановской фильтрации;

процедура формирования разносов отсчетов доплеровских частот для обучения нейронной сети;

процедура обучения нейронной сети по разносам доплеровских частот;

процедура функционирования нейронной сети при принятии решения о типовом составе ГВЦ.

На рис. 1 представлена структура оптимального алгоритма распознавания типового состава ГВЦ в БРЛС перспективного истребителя, где обозначено:

i = 1, ..., I ; I - общее количество самолетов в группе;

j = 1, ., J ; J - общее количество вариантов полета каждой i -й ВЦ из состава группы;

q = 1, ..., Q ; Q - общее количество типов самолетов в группе;

A F ij_q (k + 1 ) - разность на к шаге между значениями доплеровских частот, обусловленных отражениями РЛ-сигнала от планера ВЦ и вращающихся лопаток рабочего колеса первой ступени КНД силовой установки ВЦ;

– оценка разности на k шаге между оцененными значениями доплеровских частот, обусловленных отражениями РЛ сигнала от планера ВЦ и вращающихся лопаток рабочего колеса первой ступени КНД силовой установки ВЦ;

∆ F _ij_q – разносы доплеровских частот, обусловленных отражениями РЛ-сигнала от планера ВЦ и вращающихся лопаток рабочего колеса первой ступени КНД силовой установки ВЦ;

P ijq – вероятности предварительного распознавания q типа каждого самолета группы с каждого ij -го выхода нейронной сети;

P _зад – заданная вероятность распознавания типа каждого самолета группы.

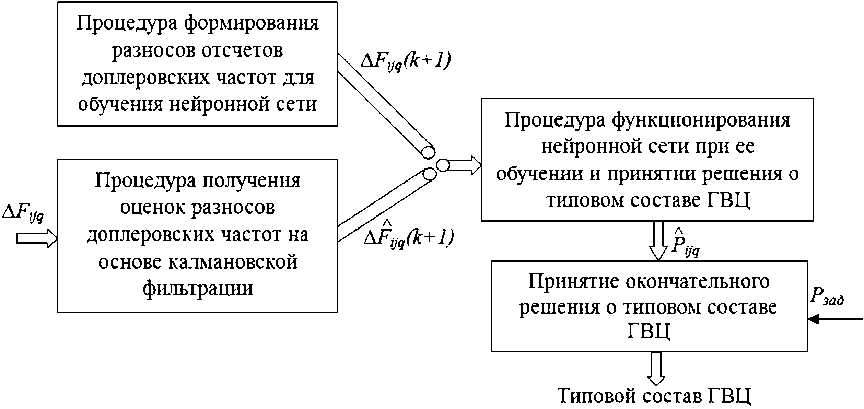
Рис. 1. Структура оптимального алгоритма распознавания типового состава групповой воздушной цели

Fig. 1. The structure of the optimal algorithm for recognizing the typical composition of a group air target

Синтез процедуры получения оценок разносов доплеровских частот (скоростей) на основе калмановской фильтрации

Физический смысл данной процедуры заключается в получении оценок разносов отсчетов доплеровских частот (скоростей) между центроидом доплеровской частоты, обусловленным отражениями РЛ-сигнала от планеров всех самолетов группы и отражениями РЛ-сигнала от вращающихся лопаток рабочего колеса первой ступени КНД двигателя каждого самолета (с ТРД) группы.

Для синтеза процедуры получения таких оценок разносов отсчетов доплеровских частот (скоростей) используем оптимальную, линейную, дискретную, многомерную, калмановскую фильтрацию, представляемую следующими дискретными уравнениями [6–9]:

Р"(к +1) = Ф(к)Р(к)Фт(к) + Q(k);	(3)
^(к +1) = Н(к)РЧк + Х)Нт(к) + R(k);	(4)
К(к +1) = Р"(к + Х^НТ (к^’^к +1);	(5)
У(Н7)=Я(^)-Х(^)+ед;	(6)
Z(k +1) = Y(k +1) - Н(к)Ф(к + Х)Х(к);	(7)

Х(к +1) = Ф(к)Х(к) + К(к + l)Z(k +1);

Р(к + !) = [/- К (к + 1)Н(к^Р"(к +1),

где P(к + 1) и P ( к + 1) — ковариационные матрицы ошибок экстраполяции и фильтрации соответственно, размерности n х n ( n — размерность вектора Х(к+1) состояния);

Ф(k) – переходная матрица состояния размерности n х n ;

Q(k) и R(k) – ковариационные матрицы шумов возбуждения и наблюдения размерности n х n и m х m (m — размерность вектора Y(k+1) наблюдения) соответственно;

ϒ (k) – вектор-столбец шумов наблюдения, представляющие собой гауссовские «белые» последовательности с нулевыми математическими ожиданиями и матрицами спектральных плотностей N г ( к ) размерности m ;

Н(k) – матрица наблюдения (измерения) размерности m х n ;

Z(k+1) – матрица невязок измерения размерности m ;

K(k+1) – матрица весовых коэффициентов размерности n х m ;

I – единичная матрица размерности n х n ;

«т» – символ транспонирования;

«-1» – символ нахождения обратной матрицы;

«^» – символ нахождения оценки.

Определим далее размерности матрицы значения их элементов, входящих в процедуру калмановской фильтрации (3) – (9).

Основу синтеза процедуры получения оценок разносов отсчетов доплеровских частот (скоростей) при использовании калмановской фильтрации составляет их динамическая модель, которая представляется в виде системы дифференциальных уравнений (д.у.). С этой целью составим следующую систему д.у. для i -го самолета из состава группы с j -м характером полета и имеющим q -й тип:

А^(0 = ^(0,А^(0) = А^;

a_uq(0 = -а^уДО - ^A^(Z)

Kyq(O = O,K^(O) = Koqq, где Vijq и ∆Vijq – детерминированная и флюктуационная составляющие разноса скоростей (доплеровских частот) между центроидом планерных составляющих скоростей всех це-лей группы и вращающимися лопатками рабочего колеса первой ступени компрессора низкого давления (КНД) i-й ВЦ из состава группы, имеющая j-й характер полета и q-й тип;

a ijq - флюктуационная составляющая разносов ускорений (производных доплеровских частот) между центроидом планерных составляющих скоростей всех целей группы и вращающимися лопатками рабочего колеса первой ступени КНД i -й ВЦ из состава группы, имеющая j -й характер полета и q -й тип;

α ijq – величина, обратно пропорциональная времени корреляции τ ijq разноса скоростей (доплеровских частот) i -й ВЦ из состава группы, имеющая j -й характер полета и q -й тип, определяемая как

;                                                                                      (11)

уд

β ijq – квадрат собственной частоты f ijq автокорреляционной функции разноса скоростей (доплеровских частот) i -й ВЦ из состава группы, имеющая j -й характер полета и q -й тип, определяемая как

3„=(2C>2-О

σ ijq – среднеквадратическое отклонение (СКО) разносов скоростей (доплеровских частот) i -й ВЦ из состава группы, имеющая j -й характер полета и q -й тип, определяемое как

;(13)

V9         vijq ijq V J l]q 7 J’ nijq – формирующий белый гауссовский шум с нулевым математическим ожиданием (МОЖ) и единичными интенсивностями разносов скоростей (доплеровских частот).

Систему д.у. (10) в векторно-матричном виде можно представить следующим образом:

• X.„ = A,MX1M + G^N.^XW = '.(14)

где X ij_q и X _0ijq — соответственно истинный вектор состояния и его начальное условие размерности 3 х 1, имеющие вид

;

;

где А ijq — известная матрица размерности 3 х 3, имеющая следующие, отличные от нуля, элементы (для сокращения записей индексы i, j и q для обозначения элементов соответствующих матриц будут опущены) a 12 = 1; a 21 = - p tjq ; a 22 = — a jq ;

G ijq – матрица размерности 3х3, имеющая ненулевой элемент                ;

N ijq = | 0, n jq ,0| ^т - транспонированный вектор формирующих белых гауссовских шумов с нулевым МОЖ и единичной интенсивности, имеющий размерность 3 х 1.

Элементы матрицы наблюдения в уравнении (6) будут определяться, с одной стороны, составом измерителей функционально связанных координат, а с другой - условием наблюдаемости фильтра, которое необходимо обеспечить для предотвращения его расходимости. Исходя из этого ненулевыми элементами матрицы наблюдения Н _ij_q (k) в уравнении наблюдения (6), имеющей размерность 1 х 3, будут являться h 11 = h ₁₃ = 1.

Элемент вектора шума наблюдения Y j_q (k) , имеющего размерность 1 х 1, является некоррелированным с элементом вектора шумов возбуждения N j_q .

Для определения элементов матриц Ф ijq (k) и Q ijq (k) осуществляется переход от векторноматричного дифференциального уравнения (14) в непрерывном времени к уравнениям в дискретном времени в соответствии со следующими соотношениями [10]:

ф„„(к) = ехР(А,,Л ).                                 (15)

,,.,№ =                     ,                                             (16)

№+DA

J_ljqW = J <^Д(* + 1)Г-г]€7^^,                (17)

где Т – период дискретизации.

На практике, как правило, ограничиваются линейными членами при определении матриц Ф ijq (k) и Q ijq (k) [10], т.е.

Ф ijq (k) « I + A ijq T.                                                                      (18)

В результате матрица Ф ^ (к), имеющая размерность 3 х 3, будет иметь следующие отличные от нуля элементы: ф _п = ф 33= 1; ф 12= Т ; ф 21= - Ф ^ Т ; Ф 22= 1 — ф ^ Т

После ряда преобразований, определяемых формулами (15), (16) и (17), и ограничений линейными членами ненулевым элементом ковариационной матрицы Q ijq (k) шумов возбуждения размерности 3 х 3 будет являться

Элемент вектора Y ( к + 1) наблюдения имеет вид

• v,.^ + D = \У„Дк + 1) + bVJk + 1)] + У1га(к + 1);(19)

элемент вектора Z ( к + 1) невязок измерения имеет вид

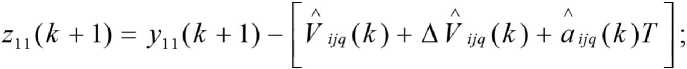
элементы вектора           оценок имеют вид

^и(дк +1) = ^и(дк) + auq (k)T + ки(к + Пг.лк +1);(

Яуд(к + 0 = 0 - «yq^ijq^ " ^Uq^^qW + ^к + W^ + ^

bN^ + 1) = NljqW + ки(к + V)zn(k + 1).(

На рис. 2 представлена структура калмановского оптимального линейного фильтра.

Процедура получения разносов доплеровских частот для обучения нейронной сети

С целью обучения нейронной сети сформируем обучающие выборки разносов доплеровских частот A F ijq ( к +1) для различных типов самолетов с ТРД с различным характером их полета, исходя из выражения

№4k^ = awx^.(24)

Представим динамическую модель (систему д.у.) (10) в виде разносов не скоростей, а доплеровских частот как

;

;(25)

кд1>=-“.><,к1у^^,№,,^+^к^уу^^, где (по аналогии с (10)):

F ijq и A F ijq — соответственно детерминированные и флюктуационные составляющие разносов доплеровских частот для каждого i –го самолета группы, имеющего j -й характер полета и q -й тип;

• – производные разносов доплеровских частот для каждого i –го самолета группы, имеющего j -й характер полета и q -й тип;

• α _ij_q – величины, обратно пропорциональные временам корреляции разносов доплеровских частот для каждого i- го самолета группы, имеющего j -й характер полета и q -й тип;

• β _ij_q – квадраты собственных частот автокорреляционных функций разносов доплеровских частот для каждого i –го самолета группы, имеющего j -й характер полета и q -й тип;

• σ _ij_q – среднеквадратические отклонения производных разносов доплеровских частот для каждого i –го самолета группы, имеющего j -й характер полета и q -й тип;

• n _ij_q – взаимонезависимые формирующие «белые» гауссовские шумы с нулевыми МОЖ и единичными интенсивностями для каждого i –го самолета группы, имеющего j -й характер полета и q -й тип, вектор состояния в соответствии с динамической моделью (25) определяется как

  
  

x(t) = । F j ( t ), a F ijq ( t ), ^цт.

Шумы возбуждения

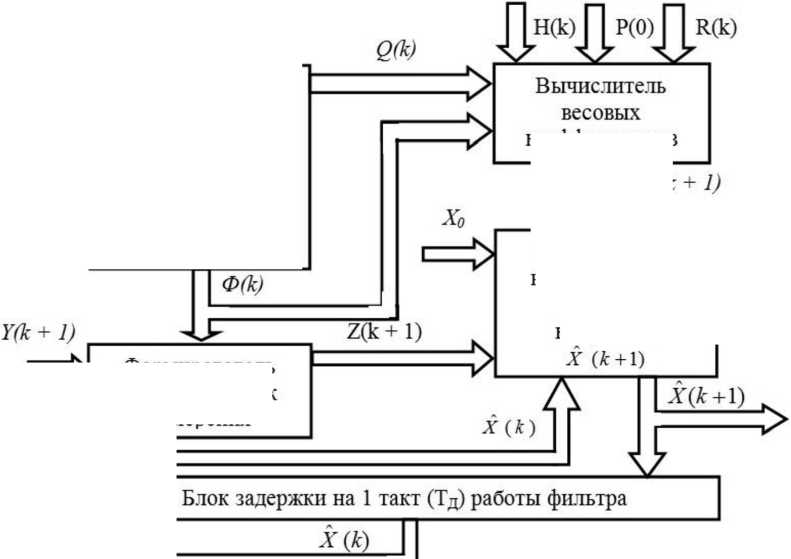
Рис. 2. Структурная схема калмановского фильтра

Fig. 2. Block diagram of the Kalman filter

Формирователь матриц Ф(к) и Q(k) на основе динамической модели (системы д.у.)

коэффициентов

K(k

Формирователь вектора оценки фазовых координат

Формирователь

А вектора невязок ^у измерения

Переходная матрица состояния размерности 3 х 3 в соответствии с динамической моделью (25), ее отличные от нуля элементы имеют следующие значения:

ф 11 = ф 22 = 1; ф 23 = т ; ф 31 = - в^т ; ф зз = 1 - a _tj_q T .

Согласно (24) и (25) формируются последовательно в дискретном времени разносы доплеровских частот в виде

Д5„,«- + 1) = Е„ ОО + Д5„ »О№-«,ТУ_#ОТ - 0_ИТ⁵ЬР„ОО. (28) где к = 1,..., К - текущий такт формирования разносов доплеровских частот;

К – общее количество тактов формирования разносов доплеровских частот, по которым в течение К тактов осуществляется предварительное обучение нейронной сети для различных типов целей с различным характером их полета, имеющих соответствующий разнос доплеровских частот ΔF ijq (k+1).

Процедура функционирования нейронной сети в режимах «обучение» и «принятие решения» о типовом составе групповой воздушной цели

В задачах распознавания при обучении нейронной сети широко используются методы градиентного спуска. Для многослойных нейронных сетей, использующих обучение с учителем обучения, применяется алгоритм обратного распространения ошибки [17–19], который можно рассматривать как обобщение алгоритма адаптивной фильтрации - минимизации среднеквадратической ошибки.

Обучение нейронной сети предполагает два прохода по всем ее слоям (рис. 3).

При прямом прохождении входной вектор, в который входят разносы доплеровских частот ΔF ijq (k+1) , подается на сенсорные узлы сети (нейроны), после чего распространяется по сети от слоя к слою. В результате генерируется набор выходных сигналов, который и является фактической реакцией сети на данный входной вектор. Во время прямого прохода все синаптические веса (весовые коэффициенты) сети фиксированы.

Во время обратного прохода все синаптические веса настраиваются в соответствии с правилом коррекции ошибок, а именно фактический выход сети вычитается из желаемого (целевого) отклика, в результате чего формируется сигнал ошибки. Этот сигнал впоследствии распространяется по сети в направлении, обратном направлению синаптических связей. Весовые коэффициенты настраиваются с целью максимального приближения выходного сигнала сети к желаемому в статистическом смысле.

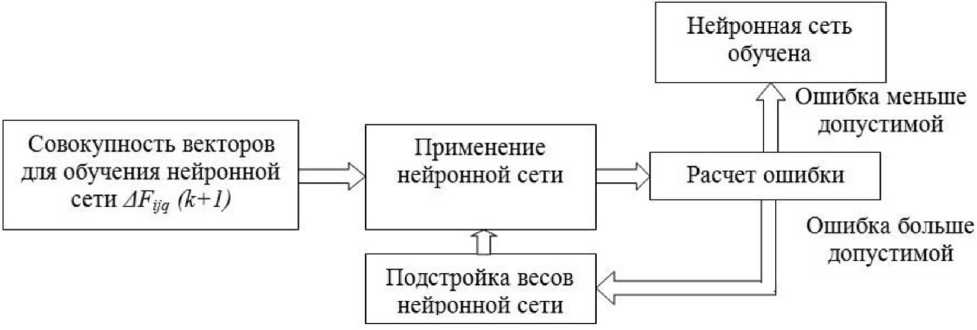
Рис. 3. Алгоритм обучения нейронной сети

Fig. 3. Neural network learning algorithm

Функция ошибки нейронной сети для каждого k -го разноса доплеровских частот ΔF _ij_q (k) рассчитывается как [19]

Е^ЦД^-^ ,                    (29)

где - реальное выходное состояние z -го нейрона выходного слоя N нейронной сети при подаче на ее входы k -го разноса доплеровских частот ΔF ijq (k);

d _z – идеальное (желаемое) выходное состояние z -го нейрона выходного слоя.

Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью разносам доплеровских частот AF ijq (k). Минимизация ведется методом градиентного спуска, что означает подстройку весовых коэффициентов следующим образом:

^<=-'Г— ,                               (30)

где w tz – весовой коэффициент синаптической связи, соединяющей z -й нейрон слоя n – 1 с t -м нейроном слоя n ; η – коэффициент скорости обучения, 0 <  η < 1.

В выражении (30)

5Е дЕ 5sz 5wlz 5sz 5wtz

где s z – взвешенная сумма входных сигналов нейрона z, слоя n , то есть аргумент активационной функции

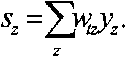
Из формулы (31) величина ' -равна выходу нейрона предыдущего слоя у?'-1*. Что каса- ется первого множителя, он раскладывается следующим образом:

_ ^ 5Е 5su

5sz и dsu dsz

Здесь суммирование по и выполняется среди нейронов слоя n + 1.

Введя новую переменную

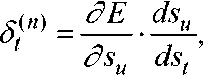
получим рекурсивную формулу для расчетов величин слоя n из величин старшего слоя n + 1:

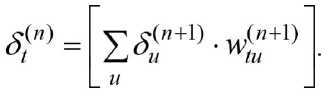
Таким образом,

^^-П-З^М"^

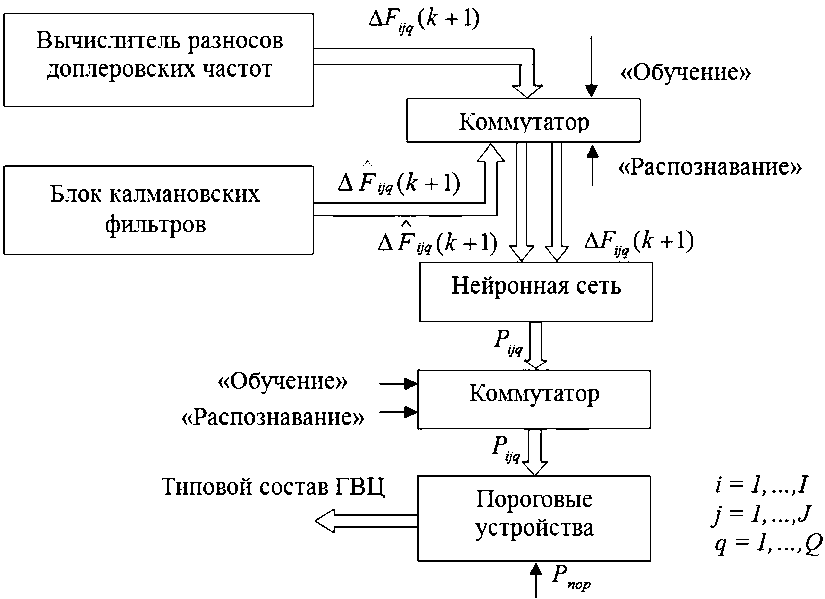
Рис. 4. Структура функционирования нейронной сети в режимах «обучение» и «принятие решения» о типовом составе групповой воздушной цели

Fig. 4. The structure of the neural network functioning in the «training» and «decision-making» modes on the typical composition of a group air target

После определения оптимальных значений всех переменных весовых коэффициентов нейронная сеть считается обученной и готовой к функционированию.

В режиме «принятие решения» на предварительно обученную нейронную сеть поступают оценки отсчетов разносов доплеровских частот ^F^k + l) (рис. 4) между центроидом планерных составляющих всех целей группы и вращающимися лопатками рабочего колеса первой ступени компрессора низкого давления i -й ВЦ из состава группы (21), формируемых на выходе каждого ijq -го калмановского фильтра, функционирующего в соответствии с процедурой (3)–(9) с динамической моделью (10).

За К тактов работы калмановских фильтров соответствующие вероятности Р ijq предварительного распознавания типа каждого самолета группы с каждого выхода нейронной сети поступают на соответствующие входы пороговых устройств.

В каждом пороговом устройстве соответствующие значения вероятностей Р ijq сравниваются с пороговым значением Р _пор, при выполнении условия для каждого значения Р _ij_q ≥ Р _пор принимается окончательное решение о том, что в группе находится i -й самолет группы, имеющий j -й характер полета и q -й тип, в противном случае принимается решение об отсутствии данного типа самолета в группе.

Результаты моделирования оптимального алгоритма распознавания типового состава групповой воздушной цели

В ходе моделирования нейронная сеть была обучена при условии, что общее количество самолетов с ТРД в группе равно 4 и возможно нахождение в группе 8 типов самолетов (типы

Таблица. Результаты имитационного моделирования

Table. Simulation results

№ цели	Вероятности распознавания типа каждого самолета с ТРД в группе
	Тип 1	Тип 2	Тип 3	Тип 4	Тип 5	Тип 6	Тип 7	Тип 8
1	0.94;0,97	0,1;0,12	0,08;0,1	0,11;0,13	0,09;0,11	0,13;0,15	0,15;0,16	0,12;0,14
2	0,18;0,2	0,94;0,97	0,19;0,21	0,17;0,19	0,2;0,22	0,14;0,0,18	0,21;0,24	0,15;0,18
3	0,23;0,25	0,15;0,16	0,95;0,97	0,11;0,13	0,1;0,12	0,13;0,15	0,18;0,2	0,09;0,11
4	0,19;0,21	0,09;0,11	0,18;0,2	0,94;0,97	0,12;0,14	0,14;0,0,18	0,15;0,16	0,13;0,15

1–8), радиолокационные сигналы от которых были зарегистрированы и обработаны, то есть I =4, J =8.

Пороговое значение вероятности принималось равным Р _пор=0,9.

Величина дискрета – Т =0,1с.

В результате моделирования за 14–15 тактов ( К =14–15, то есть за время 1,4–1,5 с) работы калмановских фильтров были получены следующие результаты (с доверительной вероятностью 0,95), приведенные в таблице.

Из анализа полученных результатов имитационного моделирования следует, что с вероятностью 0,94–0,97 (превосходит пороговое значение Р_пор=0,9) в группе находятся самолеты с ТРД типа 1, 2, 3 и 4, что соответствует действительности (именно оценки реальных разносов отсчетов доплеровских частот для этих типов самолетов подавались на ijq -е входы нейронной сети).

Во всех случаях вероятности ложного распознавания типов 1, 2, 3 и 4 составили порядка 0,022–0,03.

Выводы

• 1.    Синтезирован оптимальный алгоритм распознавания типового состава ГВЦ из класса «самолеты с ТРД» на основе калмановской фильтрации и нейронной сети, который включает процедуры: получения оценок разносов доплеровских частот на основе калмановской фильтрации; формирования разносов отсчетов доплеровских частот для обучения нейронной сети; обучения нейронной сети по разносам доплеровских частот; функционирования нейронной сети при принятии решения о типовом составе ГВЦ.

• 2.    Путем моделирования и с учетом экспериментальных исходных данных получены характеристики синтезированного оптимального алгоритма, при этом обеспечивается постоянство вероятности распознавания типа каждого самолета с ТРД в их группе независимо от характера его полета.