Синтез оптимального управления движением наводимого летательного аппарата на маневрирующий космический объект

Современное состояние международных отношений выдвинуло на передний рубеж актуальную для России и ее союзников военно-политическую проблему – реагирование на возможное размещение США оружия в космосе. На Космическом симпозиуме 11 декабря 2024 года глава Космического командования США генерал Стивен Уайтинг призвал к развертыванию оружия в космосе [1].

Большую угрозу для Российской Федерации составит размещение высокоточного оружия в космосе, которое может быть применено для нанесения ударов как по космическим, так и по наземным стратегическим объектам. Повышается боевая устойчивость средств поражения противника благодаря расширению видов базирования, высот, скоростей их применения, а также возможность совершать маневр.

Размещение вооружения в космосе сокращает подлетное время средств поражений до важных стратегических объектов Российской Федерации, что, в свою очередь, значительно ограничивает

I/ I— ОСМИНЕСКИЕ АППАРАТЫ VI технологии вин время для организации парирования угроз и ответного удара отечественных стратегических ядерных и не ядерных сил до неприемлемого уровня из-за снижения возможностей систем противодействия [2].

Таким образом, в условиях возможного размещения оружия в космосе требуется разработка новых или модернизация существующих средств противодействия, способных эффективно отразить нападение.

Для решения данной задачи предложен синтез оптимального управления движением наводимого ¹⁷⁸ летательного аппарата (ЛА) на маневрирующий космический объект (КО) для увеличения точности наведения.

1. Построение области достижимости летательного аппарата

_________________________ № 3 (53) ^2О25

Том 9

нат, связанной с его центром масс; g – ускорение силы тяжести; m ₀ - начальная масса; m _с - секундный расход массы; P – тяга двигательной установки.

В векторно-матричном виде выражение (1) запишется в виде:

dx I dt=F(x(t),a (t)), где: x = [ V, 3, y, x ]T - вектор состояния ЛА в вертикальной плоскости; F = [fV, fθ, fy, fx]T – вектор-функция, определяемая правыми частями выражения (1); α – управление, представленное углом атаки.

Величины углов отклонения двигателей управления и возникающие ввиду этого углы атаки ЛА функционально связаны, поэтому примем за управление угол атаки, который удовлетворяет ограничению:

|а\ <  а                             (2)

Для оценки возможностей по динамике целевого объекта будем использовать цикличное построение областей достижимости. Это необходимо, поскольку методы наведения в упрежденную точку встречи с баллистической целью не могут обеспечить необходимую точность поражения, так как для маневрирующих целей невозможно рассчитать такую точку встречи ввиду отличия закона движения цели от баллистического (эллиптического) [3].

В работе [5] предложен метод расчета такой области для аэродинамической цели на конечном этапе телеуправления без работающей двигательной установки.

Рассмотрим аналогичным образом для вертикальной плоскости полета построение областей достижимости маневрирующей цели на заатмос-ферном участке при работающей её двигательной установке. Для горизонтальной плоскости задача

Задано начальное положение ЛА:

1 0 = 0, V (0) = V o , 0 (0) = 0 0 , У (0) = y 0 , X (0) = X o . (3)

Задан момент θ, на который рассчитывается область достижимости ЛА.

Областью достижимости (ОД) управляемой системы (1) в k -мерном пространстве { x 1 x ₂ x ₃ ... x _k} ( k < n ) из начального состояния (3) в момент времени & ( £ >  1 ₀) при ограничении на управлении (2) называется множество G ( 1 ₀, x ₀, U , & ) тех и только тех точек q = { x 1 ( & ), x ₂( & ),..., x _q( & ),}, в которые можно перевести систему из начального состояния х ₀ в момент времени &  за счет выбора функции управления u ( t ) = ^а (t) , удовлетворяющей заданным ограничениям [5].

Здесь U – множество функций управления, α – угол атаки, l – единичный вектор, направление которого определятся углом ξ₁ между вектором l и осью OX определяется.

решается аналогично.

Движение целевого объекта на заатмосферном участке в вертикальной плоскости с работающим двигателем определяется следующей системой дифференциальных уравнений [7]:

dV dt

P

⁽ m 0 - m c t )

- g sin( ^ )

d 0 dt

P a

⁽ m o - m c t^{) V} )

- g cos( 0 )I V

dx

— = V cos( 0 ) dt

d=V ^{sin( 0 )}

где V – скорость; θ – угол наклона траектории; x (дальность) и у (высота) - координаты местоположения ЛА в неподвижной системе коорди-

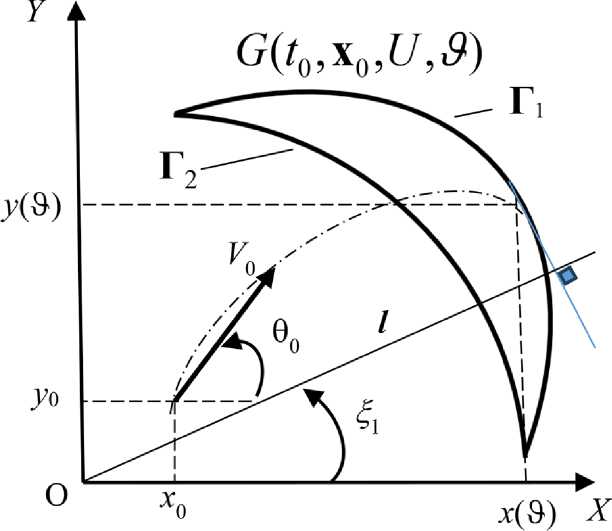
Рисунок 1. Область достижимости летательного аппарата

ОД ЛА в плоскости ограничена двумя кривыми Г1 – выпуклая часть границы, Г2 – вогнутая часть границы.

Для расчета точек на выпуклой части границы ОД решается следующая задача оптимального управления.

Требуется найти порядок изменения угла атаки α( t ), обеспечивающей максимальное смещение ЛА из начальной позиции ( V 0 , 0_О, x ₀, y ₀, m о , m _с, R ) в вертикальной плоскости в направлении единичного вектора l в момент времени ϑ при выполнении условий (2).

Для решения задачи по аналогии с [5] используем принцип максимума Понтрягина. Принцип утверждает существование вектор-функции Ψ( t ), являющейся решением системы уравнений:

d„ / dt = -дH / дx, где    H (t, x (t),„ (t), й( t)) = у т F    - функция

Гамильтона, и ( t ) - оптимальное управление.

Систему уравнений d x

F ( t , x , u )

.          „ _jjh j                    dt ax

H ( t , x ( t ), „ ( t ), й ( t )) = max „ ( t ) , U H ( t , x ( t ), „ ( t ), u ( t))

называют п-системой. Решение п-системы является решением задачи оптимального управления.

Выпуклая граница ОД ЛА строится по точкам посредством последовательного задания углов ξ₁ и решения задачи о максимальном смещении ЛА вдоль заданного вектора l направления. То есть требуется максимизировать скорость ЛА в заданный момент ϑ при его выведении по направлению вектора l .

Показатель оптимальности в данном случае будет иметь вид:

J = V ( ,               (4)

Для использования традиционной формы принципа максимума вместо максимизации скорости в момент д будем искать минимум следующего функционала J 1 = - V ( д ), что, очевидно, равнозначно.

Функция Гамильтона для системы (1) с терминальным критерием имеет вид:

R                  R a

^H = ^-„v------- ^-„ v g ^sin ( 0 ) „ 7------ ^-

2 m c t                ( m 0 ^- m c t ) ^V

„ gcoVJL+yVsin(0)+„XVcos(0).

Составим сопряженную систему уравнений:

^

d „  д H

-=- =--= „ dt     д V 06

R a

7------ A—„ ^- „ 0

⁽ m 0 ^- m c t ) ^V

g ^cos ( ⁰ )

—-^ ^- „ y sin ^{0 -} „ cos ⁰ ;

V ^{2 y}

„ _JJ H _—, g sin 0 d,- ^{s 0}-    ⁰ V

„ dt

„ dt

+ „ _Vg cos 0 - „ _yVcos 0 + „ _xVsin 0 ;

-

dH = 0; sx ah M

_ 0

Рассмотрим условия трансверсальности для фиксированного момента ϑ :

где

дJ, --+ Lsw 1 „ T t =, 5 w, = 0, “дJ ’ д V V „V 8V,       дJ 0 „0 80, дj   д0 w _ ;„; = ;dw„ = y „y Sy, Sw  J x „X 8x3_        дУ дJ дx

I/ - J—

ОСМИЧЕСКИЕАППАРАТЫ И

технологи и^нв

Том 9

Это условие в развернутом виде имеет вид:

[-1+¥г (»№+^ (,) зе, + v у (э)8уа +

+ ^ , ( , ) З х _а = 0.

Так как при t = ϑ фазовые координаты V , θ , γ , χ могут принимать любые значения, то в силу независимости вариаций δV _ϑ, δθ _ϑ, δγ _ϑ, δχ _ϑ получаем следующие граничные условия для фазовых координат сопряженной системы:

a*( t ) = We

R

( ^m 0 ^_ met ) ^V

к ⁽ ^ ) = 1; w e ( ^ ) = 1; К х И = о; V , И = 0;

Систему (5) с учетом (6) представим в виде:

dw

— = ^ ( t , w, v ^{, a} ) , dt

гдe ¥ =

wv

W e J

r^v (t. w,va)] , ^t, w,w,a =

^,         ^ ) | % ( t,w, w , a ) J

;

к (t, wwa) = We

___Ra__

⁽ m о ^- mJ ) V ²

_    g cos ( e ) _;

W"   V2

g sin e

, e ⁽ t , w ^w , « W e — ^^wv ^{g cos e}

Согласно принципу максимума функция Гам ильтона должна при оптимальном управлении достигать максимума. Причем управление α( t ) должно удовлетворять ограничению (2) [6].

Функцию Гамильтона представим в следующем виде:

^н=^н о + H , a .

где

Н- К . -R- _ , . g sin e Vw, g =®.

^- m     R

“ ' = ^Г " ( m. - mg ) V

Функц ия H до стигает максимума при сле дующих значениях управления:

Режим особого управления возникает при ψ _θ = 0, в этом случае режим особого управления должен продолжаться до окончания управления движения. Но в момент 3 в систему граничных условий ψ _v ≠ 0, поэтому режим особого управления в данной задаче не может появиться.

Таким образом, π-система в данном случае включает системы уравнений (1). (7) и соотношения выбора оптимального управления (8), π-система удовлетворяет начальным и граничным условиям и условиям (6).

Для решения краевой задачи могут быть использованы различные известные методы динамического программирования, например, как в [5], модифицированный метод Ньютона. Задаваясь различными углами ^ ориентации вектора l . соединяя полученные точки. можно получить выпуклую границу Г ₁ ОД ЛА. Крайние точки границы можно получить. выбрав управление с неизменным в течение полета максимально допустимым управлением ±α_доп. [8]

Вогнутую границу Г ₂ ОД ЛА можно построить также по точкам аналогично Г ₁, решая задачу о минимальном смещении ЛА в заданном направлении.

Программная реализация вышеуказанного алгоритма. позволяющая построить области достижимости заатмосферного ЛА. показывает зависимости величины ОД от скорости и массы ЛА при фиксированном угле атаки α. На рисунке 2 показан результат построения ОД для различных значений модуля вектора скорости: 1 км/с, 3 км/с, 5 км/с, 7 км/с при фиксированных остальных значениях.

2. Построение графиков вектора состояния целевого объекта

Для вычисления координат точки наведения проинтегрируем систему уравнений (1) в программной среде Mathlab . тем самым получим изменение вектора состояния ЛА на заданный промежуток времени в зависимости от выбора характе ристик ЛА с постоянным углом атаки.

Для расчета скорости целевого объекта воспользуемся следующим выражением:

О доп'

/^^

^{a (} t ) =

-^а доп'

если H >  0;

если Н <  0;

режим особого управления, если Н = 0,

Отк уда

d Н

da

= 0.

. *

К

⁰ ^ R 3 +Н ц ) .

где V 0 - начальная скорость ЛА. k - гравитационная постоянная, R з – радиус Земли, Hц – высота орбиты.

Тогда. предполагая высоту орбиты 500 км. начальная скорость участка маневрирования будет

Рисунок 2. Области достижимости ЛА при увеличении модуля вектора скорости при фиксированном значении угла атаки

равна V 0 = 7,61 км/с. P = 5000 Н, m ₀ = 2000 кг, m _с = 3 кг/с, g = 9.8 м/с², t = [1.20] с, a = 10 о , 0 ₀ = 0.

Подставив данные значения в начальные условия, получим изменение вектора-состояния при постоянном угле атаки (рисунок 3).

Исходя из графиков на рисунке 3 видно, что точка прицеливания сместилась в вертикальной плоскости на 2 км, скорость увеличилась на 0,046 км/с, угол наклона вектора скорости относительно касательной – на 0,025 рад (1,5о).

Заключение

Для повышения точности наведения летательных аппаратов на конечном участке необходимо применять методы самонаведения, из которых наиболее часто применяемым на практике является метод пропорциональной навигации [10]. При этом важным условием реализации метода является задание необходимых начальных условий, определяемых конеч-

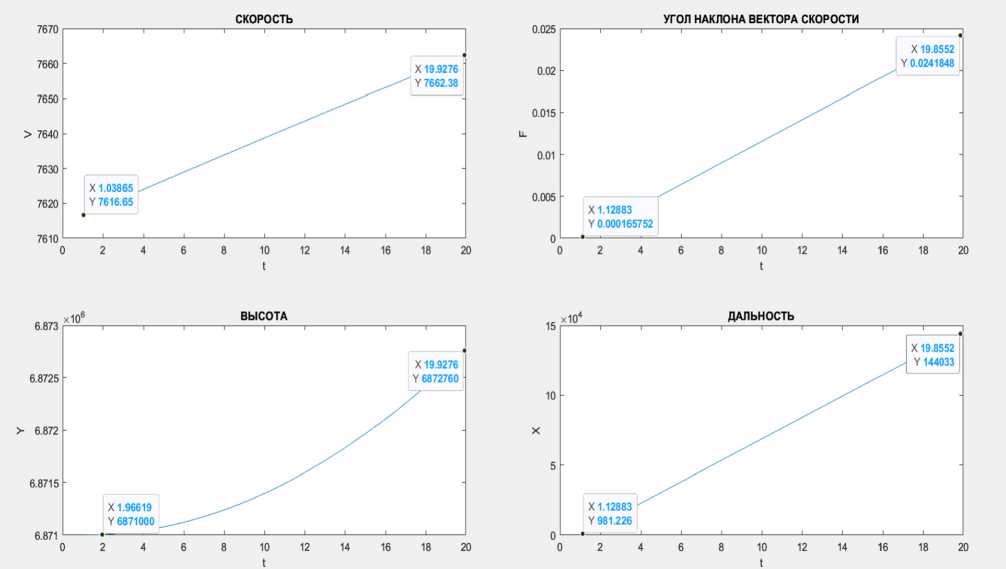
Рисунок 3. Изменение параметров вектора-состояния летательного аппарата за 20 секунд

АППАРАТЫ VI технологи ш^ин

ными параметрами предшествующего дальнего наведения.

Предложенный алгоритм синтеза оптимального управления на основе принципа Л. С. Понтрягина, рассмотренный на примере управления движением наводимого ЛА в плоскости тангажа при заданных времени полёта, конечных координатах, величине и ориентации его вектора скорости, обеспечивает минимизацию заданного критерия качества [11].

Найденный результат решения задачи оптимального управления полётом наводимого лета- ¹⁸² тельного аппарата и космического объекта наведе-

Том 9

ния заключается в определении наиболее выгодных условий для начала этапа самонаведения с использованием оптико-электронных систем. Установлено, что одно из наиболее важных условий для начала реализации метода пропорциональной навигации – обеспечение ориентации векторов скоростей ЛА и КО по их линии визирования [9].

Дальнейшим направлением исследований является синтез управления летательным аппаратом с переменным профилем тяги двигательной установки, позволяющий осуществлять поиск оптимального управления на отдельных временных участках его полёта.