Синтез оптимального управления квантомеханической системой

Многие математические задачи оптимизации систем с линейными управлениями относятся к классу вырожденных задач оптимального управления [1] , которые характеризуются присутствием явных или скрытых пассивных дифференциальных связей или дискретных цепочек. Их исключение, упрощая задачу, понижая ее порядок, не меняет искомого решения. Соответствующая ему траектория оказывается магистралью , т. е. инвариантной относительно всех или части граничных условий. Магистральное решение может быть в точности искомым оптимальным, либо использоваться как эффективное начальное приближение в той или иной итерационной процедуре оптимизации. Такие решения характерны для многих приложений [1 –4] . В [4, 5] систематически исследуются вырожденные задачи оптимального управления линейной колебательной системой и достаточно общей периодической системой на неограниченном промежутке времени.

В данной статье процедуры, представленные в [4 , 5] , применяются к поиску магистральных решений характерной задачи того же класса на известной квантомеханической модели Ландау-Зинера [6] , которая

Работа выполнена при финансовой поддержке РФФИ (проект 09-01-00170-а).

представляет самостоятельный интерес и также рассматривается как прототип значительно более сложных задач этого класса, решаемых весьма перспективным методом нелокального (глобального) улучшения управления [7 –10] .

• 1.    Постановка задачи

Рассматривается следующая модель управляемой системы 4,3-2   3  4

z = wz + uz , z = wz — uz ,

• (1)             z ³ = — wz¹ — uz ¹ , z ⁴ = — wz ¹ + uz ² ,

• 2.    Решение задачи

которая представляет в действительных переменных содержательную модель Ландау-Зинера, описывающую 2-спиновую систему в терминах уравнения Шредингера в комплексных переменных [6] .

Здесь u –– управление, которое принимается неограниченным, ω–– константа, аргументом служит «замедленное время» t = ~т , где т — физическое время, ~ –– постоянная Планка. Особенность этой системы, как показано в [8] ,—наличие инварианта | z | ² = C . Ставится следующая задача оптимального управления:

t G [0,t F ], z(0) = z i , I = F(z(t F )) ^ inf, F (z) = C — (z T z * ) ² , z ∗ –– некоторое заданное состояние.

Нетрудно видеть, что соответствующая (1) предельная система [2] представляет собой совокупность двух осцилляторов одинаковой частоты dz1/dT = z3, dz^/dT = —z1,

dz2/dT = —z4, dz4/dT = z2, и имеет 3 первых интеграла [4]

y ¹ = (z 1 ) ² + (z ³ ) ² , y ² = (z ² ) ² + (z ⁴ ) ² , y ³

(два интеграла энергии и фазовый сдвиг), из которых с учетом инварианта независимы лишь два, так что имеют место следующие об- ратимые соотношения:

z1 = Vy1 cos ^, z3 = Vy1 sin 6, z"2 = Vy1 sin(6 + y3),  z4 = yfy1 cos(6 + y3), y1 + y2 = C, где θ — угловая координата точки z на интегральной траектории.

В соответствии с теорией [2] перейдем к эквивалентной производной задаче, уравнения которой получаются подстановкой выражений (3) в исходную систему (1) с учетом ее инварианта (в новых переменных):

• (4)    y ¹ = 2wpy 1 (C - y ¹ ) cos(29 + y ³ ) = f 1 (y 1 ,9,y 3 ), t G [0,t F ],

C

• (5)         y 3 = ^ш ,            sin(29 + y ³ ) = f ³ (y 1 ,9,y ³ ),

y ¹ ( C - y ¹ )

У 1 (0) = y | , У 3 (0) = y ³ , F(y(t F )) ^ inf, F(y) = min F (z(y,9) .

θ

Особенность задачи, как и всех задач с терминальным функционалом, в том, что регулярное решение уравнения Беллмана располагается вне области достижимости точки абсолютного минимума функции F (y), которая в данном случае определяется на упомянутом инварианте как z = z * (y 1 , y 3 ,9 * ) в новых переменных. В пределах области достижимости управление, очевидно, может быть задано произвольно. Таким образом рассматриваемая задача синтеза разбивается на две:

• 1.    Синтез оптимального управления 9 (t,y1,y ³ ^ в задаче быстродействия –– наискорейшего попадания в заданную точку (в данном случае y _∗ ) и одновременное построение области достижимости этой точки с помощью уравнения Беллмана

max(^ y i f ¹ + ф у з f 3 ) = 1.

θ

Конкретно,

• ⁽⁶⁾                       У⁽ф у 1 g ^{1 ) 2 + (}ф у ^з g ^{3 ) 2} = 1,

• 2.    Cинтез оптимального управления, минимизирующего функционал F(y _t F ) путем решения задачи Коши

где g ¹ =²^py ^{1 ( C -} y ¹ ), g ³ = ^ _v y i ₍ C _-y i ) .

• ⁽⁷⁾            v t = У ⁽ф у 1 д ¹)^{2 + (}ф у ^з g ^{3 ) 2} ,   ^ t F ,у = ^{-F (}y⁾.

Эти задачи решаются методом характеристик в области регулярности 0 < y1 < C,  —п/2 < y3 < п/2 (при y1 = 0, y1 = C имеет место сингулярность) с использованием следующих известных уравнений [7]

• (8)        y ¹ = H p i , y ³ = H p 3 , p ¹ = —H y i , p ³ = —H y 3 ,

где

H (y 1 ,y ³ ,p 1 ,p ³ ) = max h = Р(р 1 д 1 (у ¹ )) ² + (p ³ g ³ (y 1 )) ² , θ

9(t F , • ) = arg min F(z(y, 9)). θ

Заметим, что H фактически от y ³ не зависит, так что из (8) следует, что p ³ = const.

Уравнения (8) , как известно, совпадают с уравнениями принципа максимума Понтрягина, записанными в терминах гамильтониана (1) .

Если семейство характеристик окажется регулярным в указанной области, то это будет говорить о его оптимальности. В задаче 1 (быстродействия для автономной системы 2-го порядка) это условие регулярности проверяется непосредственно путем построения фазового портрета системы, замкнутой оптимальным позиционным управлением (9) :

• (9)    arg max H = 9 : cos(29 + y ³ ) = X 1 , sin(29 + y ³ ) = X 3 ,

9(t F , • ) = argmin F(z(y,9)), х з = P 3 g 3 , X i = P 1 g 1 , θ

^H y 1 = H ¹ ( ^X 1 y i ^X 1 ^{+ X} 3 y i ^х з ) , H y ³ = ^{H 1 (} - ^X 1 ^X 3 ^{+ X} 3 ^X 1 ) .

В задаче 2 (синтеза вне области достижимости) проверка регулярности требует более сложных построений, которые здесь рассматривать не будем. Ограничимся задачей 1. Ее решение и одновременно построение границы области достижимости сводится, как известно, к интегрированию системы (8) для различных p F : | p _F | = 1, Pf : I p F | = 1,i = 1,2 и построению семейства траекторий (фазового портрета) на плоскости ( y ¹ , y ³ ).

Случай, когда y(C — у) = 0, требует специального рассмотрения. Исключив из системы (3) уравнение относительно y3 , будем иметь вторую производную задачу (первого порядка), где y3 играет роль управления. Эта задача решается непосредственно. Строятся границы области достижимости из начальной точки, которые получаются, как ее решения при cos(29 + у3) = ±1, t Е [tI,tF).

Заданная конечная точка проектируется на одну из этих границ. Соответствующий этой проекции момент t F и будет минимальным. Полученное решение удовлетворяет системе (2) в целом при у ³ = const и будет оптимальным для этой системы если у ³ = y F .

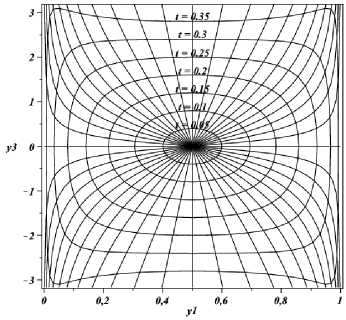
Рис. 1.

Обратим внимание, что уравнение (4) сингулярно на многообразиях у ¹ = 0 и у ¹ = C ; на этих многообразиях у ³ может быть выбрано произвольно независимо от решения на примыкающем интервале. Получающееся при этом разрывное решение реализуется как импульсное в точке разрыва последовательностью непрерывных с большим ростом производной у 3 . Отсюда следует, что если начальная или конечная точка задана на одном из этих многообразий, то полученное решение будет точным магистральным решением первой производной задачи. В итоге получается оптимальный синтез во всей замкнутой области 0 <  у ¹ <  C, — п/2 <  у ³ <  п/2.

Проиллюстрируем эти построения расчетами для двух заданных конечных точек, первая из которых выбрана из соображений симметрии, вторая соответствует примеру из работы [6] (в обоих случаях C = 1):

1)у 1 = 0.5, у 3 = 0, 2)у 1 = 0.45, у 3 = 0.28.

Расчеты выполнялись в системе Maple 12, с помощью функции Phaseportrait(). Результаты (полученные полностью в аналитическом виде ) представлены на рис. 1 –5 .

На рис. 1 –2 представлены фазовые портреты синтезированных систем. Видно, что построенное семейство характеристик регулярно всюду в рассматриваемой области, за исключением точки y ∗ (фокуса), так что в этой области задан оптимальный синтез управления

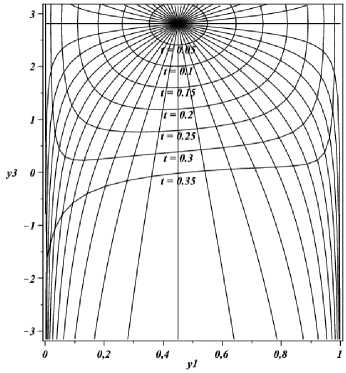
Рис. 2.

У(y ¹ , y ³ ), определяемый формулами (9) , где p 1 ,p ³ — функции (y 1 ,y ³ ) со значениями, получаемыми в процессе расчета характеристик.

На рис. 1 , кроме того, нанесены линии уровня t min = const , описывающие границу области достижимости, а на рис. 3 представлено пространственное изображение этой области.

На рис. 3 показаны множества достижимости для различных конечных точек (включая выбранные) в случае сингулярности y ¹ (1 — у ¹ ) = 0.

Таким образом, построен синтез оптимального управления в производной задаче, который задает оптимальный синтез и в исходной в форме последовательности управлений с обратной связью u(t, z) либо u(t,y,y) в новых переменных (что более удобно), с неограниченно растущими значениями управления в окрестностях точек разрыва y(t, у). Она строится по общему правилу [9] , а именно, следующим образом. Графиком 6(t,y) служит некоторое многообразие в пространстве (t, y, У), S * , которое назовем магистральным. Зададим (1/s)-окрестность S * ((1/s)-слой):

G ( S * , 1/s) = { (t,y,y): | У — У * (t,y) | < 1/s } .

При (t, У) е G ( S * , 1/s) полагаем u s = u * . В противном случае находится точка (t, y, У * ) на S * , такая, что при данном t точки (y, У * ) и

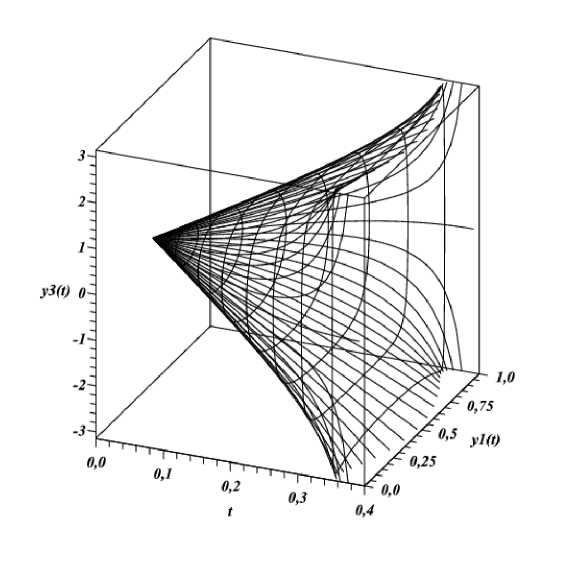
Рис. 3.

(y, 6) соединяет некоторая траектория регулярной предельной системы, то есть (2) . Далее эта траектория аппроксимируется последовательностью решений системы (1) , начинающихся из точки z . Соответствующее значение управления u s (t + 0, z) и принимается в качестве u s (t, z).

В целом последовательность функций { u s (t,x) } задает в рассматриваемой области синтез оптимального управления с любой степенью точности при достаточно большом s . Несмотря на некоторую громоздкость описанной конструкции u s (t, x), она отражает достаточно простое и наглядное правило: из любой точки (t, x), не лежащей на магистральном многообразии S _∗ , следует перемещаться с

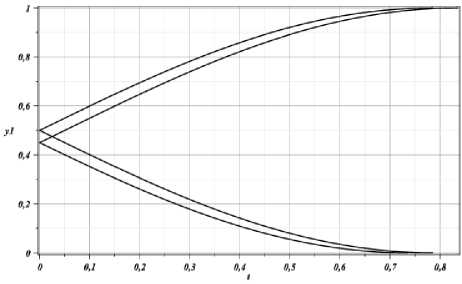
Рис. 4.

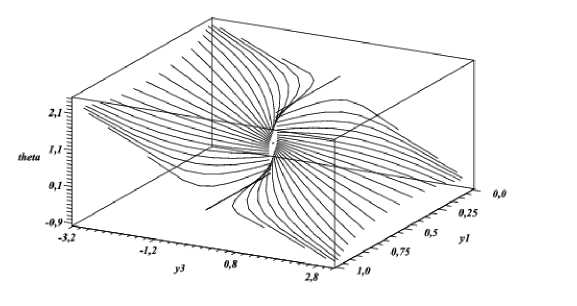
Рис. 5.

большой скоростью (в пределе — мгновенно, скачком) на это многообразие, по траектории, близкой к траектории предельной системы, а в (1/s)-okpecTHOcmu магистральной поверхности применять управление u * (t, z).

Заключение

Таким образом, полностью решена задача синтеза оптимального по быстродействию неограниченного управления на модели Ландау-

Зинера. Благодаря специфике модели эта задача четвертого порядка сводится к эквивалентной производной задаче второго порядка, а для сингулярных начальных условий –– к производной задаче первого порядка. Решение производных задач определяется точно в форме фазового портрета семейства магистральных решений, которые в исходном пространстве разрывны в граничных точках. Оно рассматривается как обобщенное решение импульсного типа исходной задачи и аппроксимируется последовательностью исходных позиционных управлений, неограниченно растущих в окрестностях точек разрыва.

Обратим внимание, что несмотря на неограниченность скоростей в исходной системе (1) , время ее перехода из одного состояния в другое заведомо не нулевое, в отличие, например от системы х ¹ = х ² , х ¹ = и, когда управление не ограничено. Это — фундаментальное свойство рассматриваемой модели как управляемой системы осцилляторов, как и более сложных моделей этого класса, так что определение минимального времени перехода имеет глубокий физический смысл.