Синтез параллельных алгоритмов преобразований Фурье-Галуа в прямых суммах конечных колец

Модулярные аналоги дискретного преобразования Фурье (теоретико-числовые преобразования, ТЧП, преобразования Фурье-Галуа)

N - 1

x ( m ) = X x ( n ) ® ^mn ( mod Р ) ® N = 1 ( mod p ) (1) n = 0

были впервые введены в работах Р.Г. Фарад-жиева и Я.З.Ципкина [1, 2] , А.Штрассена и В. Шёнхаге [3] и переоткрыты в работе Ч.М. Рейдера [4] . Последняя работа получила наибольшую известность и явилась основой для различных модификаций и обобщений ТЧП. Наибольшая популярность этой тематики приходится на 70-е годы, что объясняется, в основном, вычислительными преимуществами целочисленной арифметики для использовавшихся цифровых устройств и возможностями эффективного решения массовых задач информатики - “безошибочного” вычисления циклической свертки (целочисленных) последовательностей [5] и быстрого умножения больших целых чисел [3] . Возрождение интереса к ТЧП, наметившееся в последние годы, связано с разработкой нового поколения СБИС-устройств, использующих модулярные вычисления для реализации арифметических операций [6 - 9] .

Наиболее существенным недостатком ТЧП является то, что простые числа p c “удобной” машинной реализацией (простые числа Мерсенна, Ферма, Голомба и т.п) встречаются в натуральном ряду достаточно редко [10] , что существенно ограничивает возможности ТЧП, например, в задачах цифровой обработки многомерных цифровых массивов

(в частности, изображений).

В настоящей работе рассматривается метод синтеза параллельных алгоритмов “безошибочного” вычисления сверток целочисленных последовательностей с использованием “ТЧП-подобных” преобразований, реализуемых в кольцах классов вычетов по модулю составных чисел. Метод базируется на двух независимых и хорошо апробированных идеях:

• -    вложение кольца классов вычетов по (составному) (mod m) в прямую сумму некоторых конечных колец;

• -    представление данных в «нетрадиционных» системах счисления.

Существенно новым в рассмотренном методе является согласованный выбор конечных колец, способа вложения кольца классов вычетов в прямую сумму этих колец, а также систем счисления «с иррациональным основанием», наследующих свойства двоичной системы счисления в кольцах классов вычетов по модулям простых чисел Ферма. Аналогичная задача для вычислений в кольцах классов вычетов по модулям составных чисел Мерсенна рассмотрена автором в работе [13].

Теоретико-числовое преобразование Ферма

Исторически первым ТЧП, нашедшим эффективные применения в задачах цифровой обработки сигналов, явилось преобразование (1) при р = fs = 22s +1 = 2B +1, s = 0,1,2, 3,4. (2)

Числа fs называются числами Ферма и являются простыми только при пяти указанных значениях 5. Преобразование (1) при p = fs называется ТЧП Ферма или просто преобразованием Ферма.

Привлекательность преобразования Ферма обуславливается по меньшей мере двумя факторами:

• -    существование удобного для машинной реализации “битового” представления элементов поля ( mod f s ) c просто реализуемыми операциями сложения и умножения элементов.

• -    наличие хорошей алгоритмической поддержки вычисления преобразования (1) в виде структурно простых модулярных аналогов классического быстрого алгоритма Кули-Тьюки дискретного преобразования Фурье.

Действительно, любое целое число x из диапазона 0 <  x <  f s - 1 = 2^B может быть представлено ( B +1 ) - битовым разложением

x = x

B

2 + xB-1

B - 1

+... + X12 + Xo 2 ,

xj = 0,1.

Ассоциированный с разложением (3) ( B +1 ) - битовый вектор

< x >= ( хв , x b __b... x _b x o ) .     (4)

будем называть кодом элемента x ( mod f s ) .

Операции в кольце классов вычетов ( mod f s ) индуцируют формальные правила преобразования кодов, вполне определяемые соотношением

2 B = -1 ( mod fs )          (5)

Именно, сложение производится по почти обычным правилам двоичного сложения “с переносом в старший разряд” ; при переполнении B - го разряда “лишняя” единица вычитается из B -разрядной части результата (или, в терминах кодов, “с инвертированным знаком переносится в самый младший разряд кода) ; умножение на 2 элемента x индуцирует преобразование кодов по правилу

< x >= (xB, xB-1, ••• x 1, x0 ) a a

a a <  ^{2 x} >  ^{( x} b - 1 , ••• ^x 1 , ^x о , ^xв ); умножение элементов общего вида сводится к сложениям и умножением на степени 2.

Заметим, что код в правой части соот

ношения (5) не обязательно является битовым вектором, но может быть легко преобразован к битовому виду с использованием тривиального соотношения xj+i2j+1 = xj+i2 j + xj+i2 j. (6)

Такие векторы, преобразованные по правилу (6) к битовому представлению, будем называть редуцированными кодами и обозначать < x > * .

Далее, в отличие от поля комплексных чисел , в конечном поле ( mod p) существуют корни не любой степени N единицы, а только удовлетворяющие условию делимости :

N | | (p-1). (7)

Для чисел Ферма это стеснительное, в общем случае, ограничение (7) гарантирует существование структурно простых быстрых алгоритмов вычисления преобразования (1).

Наиболее просто реализуется преобразование (1) при ш = 2 ( mod f s ). В этом случае умножения на фазовые множители в модулярной версии алгоритма Кули-Тьюки (БПФ) реализуются без нетривиальных вещественных умножений [15] .

К сожалению, в силу соотношения (5), элемент ш = 2 ( mod f s ) является корнем степени N = 2B ( mod f s ), что ограничивает максимальную длину преобразования Ферма, реализуемого без умножений, числом N = 32 .

Кроме того, для “безошибочного” вычисления свертки спектральным методом с использованием ТЧП, число p должно быть достаточно велико [16]. В частности, при решении типичной для цифровой обработки изображений задачи вычисления двумерной свертки двух целочисленных массивов размера (512x512) с динамическими диапазонами 0 + 255, для числа p должно выполняться неравенство :

p > (512) 2 (256) 2 = 2³⁴ >  f 4 = 2¹⁶ +1.

Это существенно ограничивает возможности применения ТЧП Ферма в задачах обработки многомерной цифровой информации. Использование в качестве модулей в преобразовании (1) составных чисел Ферма доставляет серьезные трудности, связанные с существованием в модулярных кольцах по составным модулям делителей нуля и, как

следствие, с необратимостью некоторых элементов соответствующих колец и/или с не-ортогональностью базисных функций преобразования (1). Кроме того, даже при условии частичной компенсации отмеченных проблем, например, при распараллеливании вычислений в системе остаточных классов [11, 12], характерные преимущества “битовой” реализации арифметических операций именно в полях по модулям чисел Мерсенна и Ферма не наследуются для вычислений в полях по модулям целых делителей составных чисел Мерсенна или Ферма. Действительно, f5 = 232+1 = 641 -6 700 417

и сомножители уже не являются числами Ферма.

Альтернативное разложение чисел Ферма

Пусть, для определенности, число Ферма f имеет вид f = 2 B +1, B = 2r = 3t +1      (8)

и обладает свойствами:

• (а)    при всех 1 < s <  3t +1 числа f и 2 s -1 взаимно просты ;

• (b)    элемент 2(31 +1) обратим в фактор-

• кольце

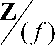
• (с)    число f не делится на 3 , то есть f Ф 0 (mod 3).

Рассмотрим кольцо S целых элементов поля F разложения полинома ф(z) = z3 + 2 над Q. В кольце S о Z для числа f наряду с обыч ным представлением составного числа в виде произведения целых рациональных чисел возможно представление в форме f = (zt 32 + 1)2y32 + 1)(2ty32 +1). (9)

где Y - примитивный корень третьей степени из единицы.

Лемма 3.1. Элементы f 1 , f₂, f ₃ е S:

f 1 = ( 2 ^{t 3} 2 + 1 ) , f 2 = ( 2 ^t γ ³ 2 + 1 ) , f 3 = ( 2 ^t γ ³ 2 + 1 )

попарно взаимно просты в кольце S.

Доказательство. Допустим, что существуют a, b 1, b2 е S, не являющиеся единицами кольца S, такие что f1 = a b 1, f2 = ab2. Нор- мальным полем для многочлена ф(z) является поле F=Q(y, З/2 ). Пусть NormYY(x) есть относительная норма элемента x е F в поле Q(Y). Трехэлементная группа Галуа полинома ф(z) над подполем Q(y) циклична и действует тождественно на Q. Относительная норма элемента

• z = x + y З/2 ^е S

равна Norm Y_Y ( z ) = x ³ +2 y ³ . Поэтому из очевидных равенств

f _; = Y f i + 1 - Y , f _; - f i = (f i —1)( Y - 1) следует

Norm Y_Y ( f 1 —1) Norm Y_Y ( Y - 1) =

= Norm Y_Y ( a ) Norm Y_Y ( b 1 - b ₂),

2 B ( YY - 1) ³ =

= Norm Y_Y ( a ) Norm Y_Y ( b 1 - b ₂).      (10)

Так как Norm Y_Y ( a ) не может быть четным числом, что противоречило бы равенству

Norm Y_Y (f 1 ) = Norm Y_Y ( ab 1 ) =

=f = 2 B +1 = Norm Y_Y ( a ) Norm Y_Y ( b 1 ), то равенство (10) может выполняться только при условии делимости

Norm Y_Y ( a ) II ( y - 1) ³ .(11)

Так как Norm Y_Y ( a ) е Q( y ), то вычисляя норму элементов (11) над Q , получаем:

Norm (Norm Y_Y ( a )) II Norm ( y -1) ³ = 27, что противоречит условию f Ф 0 (mod 3). Аналогично доказывается взаимная простота остальных элементов в условии леммы.

Пусть элементы f, f₂, f определены в лемме 3.1. Введем для удобства новые обозначения : P = f, Q= f., R = f₃ .

Лемма 3.1 гарантирует возможность представления фактор-кольца Sf в виде прямой суммы

S ≡S ⊕S ⊕S fpqr фактор-колец

SSS

/ p, /q, /г

где f = (f),

p =(P), q =(Q), r =(R) - главные идеалы, порожденные элементами f, P, Q, R, и возмож ность вложения подкольца

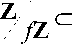
в эту

прямую сумму. Поэтому следующая лемма является частным случаем китайской теоремы об остатках [14] . Её доказательство приводится только для явного описания такого вложения.

Лемма 3. 2 . Для любого W е

Z

7f z ^су-

ществуют эффективно определяемые элемен ты X, Y, Z е

S у (f) и константы a, b, c е

^Zf- z такие, что:

• (а)    справедливо равенство

W = aXQR + bYPR + cZPQ,   (12)

причем

X = W (mod (P)), Y = W (mod (Q)), Z = W (mod (R));

• (б)    числа X, Y Z допускают представления в форме :

X = X 1 + X ₂3 2 + X ₃ 3 4;

Y = Y 1 + Y ₂ 3 2 + Y ₃3 4;

Z = Z 1 + Z 23 2 + Z ₃ 3 4;

0 < X 1 , Y 1 , Z 1 < 2 ^t+1 ;

0 < X ₂ , Y ₂ , Z ₂, X ₃ , Y ₃ , Z ₃< 2 t .

Доказательство. Соотношение (12) является следствием китайской теоремы об остатках. Для доказательства свойства (а) не- обходимо доказать, что a,b,c е

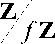
. Непос редственно проверяются равенства:

RQ = (P - 3)P + 3, PR = (Q - 3)Q + 3, PQ = (R - 3) +3.

Поэтому для выполнения равенств aQR = 1 (mod P), bPR = 1 (mod Q), cPQ = 1 (mod R) достаточно положить a = 3-1 (modf), b = 3-1 (modf), c = 3-1 (modf).

Опуская рутинные выкладки, связанные с применением метода неопределенных коэффициентов, приведем выражения для X, Y j, , Z , (j = 1,2 ,3 ) в форме:

X 1 +(-X ₃ ) 2 t ⁺¹ + X ₂ 2 ² t ⁺¹ = (3a) ^-1 W ,

Y 1 +(- Y 3 ) 2 t ⁺¹ + Y 2 2 ² t ⁺¹ = (3 b ) ^-1 W ,

Z 1 +(- Z ₃ ) 2 t ⁺¹ + Z ₂ 2 ² t ⁺¹ = (3 c ) ^-1 W .     (14)

Из соотношений (14) эффективно определяются значения X, Y, Z. Действительно, пусть % есть наименьший неотрицательный вычет для (3 a ) ^-1 W (mod f) . Пусть далее quot ( и // v ) и exc ( и // v ) - неполное частное и остаток от деления числа и на v , соответственно . Тогда, например, для X имеем:

X = exc ( х // 2 t ⁺¹ ), X ₂ = quot ( x - X , //2 ² t ⁺¹ ), ( -X 3 ) = ( x - X 1 ) 2 ^- t ^-1 - X 2 t .

Нетрудно заметить, что элементы X 2 , X 3 допускают t-битовое представление, а элемент X 1 допускает (t+1)-битовое представление.

Рассмотрим первое из равенств (13). Пусть

X, = X l 2 t + ... + X „2 0 , X₂ = X 2_A 2 t ^{— 1} + ...

1           t                      0 ⁷       2           t — 1

+ ... + X ₀2 2 0 , X₃ = X ^2' ^{— 1} + ... + X ₀ ³ 2 0 0              3           t — 1                        0

есть битовые представления элементов X 1 , X ₂ , X ₃ . Тогда соотношение (13) для X можно переписать в виде :

X = X , (V2 У + X* — , (V2 )*'^{— 1} + X , ³ — , (V2 У'^{— 2} +

+ X 1 —> f ^{— 3} +... + X 0 (3/2 у.               ⁽¹⁵⁾

Равенство (15) можно интерпретировать как представление элемента X “в системе счисления с основанием (32)”, равенства, аналогичные (15), для Yи Z - как представления элементов Y и Z “в системах счисления с основанием

у⁽ 3 2 ) ^и у⁽ 3 2 ) ”,

соответственно.

Замечание 3.1. Несмотря на не вполне привычную терминологию (“системы счисления с иррациональным основанием”), никаких “приближенных” вычислений в данной работе не производится. Элементы, обозна ченные

( 3/ 2 ) , _У( 3 2 ) и _у( 3/ 2 )

, есть просто три

различных корня уравнения W3 = 1 в фактор кольце Sf . Как будет показано ниже, такая

(неформальная) интерпретация равенства (15) позволяет ввести простые правила преобразований ассоциированных кодов

< X >= (X¹,X² — 1 ,X³ — 1 ,X¹ — ! ,...,X J ). (¹⁶)

Отметим также, что существует необходимый математический формализм для придания корректности понятию “системы счисления с иррациональным основанием”. Такие системы счисления достаточно давно и успешно применяются в информатике [17, 18] .

Арифметические действия над элемен- тами кольца yf индуцируют правила пре образования кодов (16): при сложении элементов коды преобразуются по правилу “перенос в старший разряд через две позиции”;

умножение элемента X на

(У 2 )

равносиль

но циклическому сдвигу кода с инвертированием знака младшего бита и т.д. Как и в случае обычной арифметики кольца вычетов ( mod f S ), в результате таких преобразований получаются не обязательно битовые векторы, которые, тем не менее, могут быть легко преобразованы к битовому виду с использованием соотношения (6). Такие векторы, преобразованные по правилу (6) к битовому представлению, будем также называть редуцированными кодами компонентов элемента кольца Sf и обозначать < X > * , < Y > * , < Z > * .

Шифт-преобразования Ферма

Определение 4.1. Оператор 3, определенный на множестве (к+1)-мерных редуцированных кодов, такой что

• 3 : < X > • = ( X„ X.„.Л„ X , ) • ^

• < 3 X >•= ( X , .„... X„X ,,. X , )• (17) будем называть оператором левого сдвига Ферма. Аналогично определяется оператор правого сдвига Ферма, являющийся обратным к 3 .

Следующие два утверждения, сформулированные как леммы, приводятся без доказательств.

Лемма 4.1. Для любого ( k +1)- мерного битового вектора X период последовательности < 3 ⁿ X> * является делителем числа 2( k+1 ) .

Определение 4.2. Пусть < X ( n )> • есть N - периодическая последовательность ( k +1)- мерных редуцированных кодов. Определим шифт-преобразование Ферма соотношением

N - 1

• < X(m) > * = £ 3"^т<  X (n) > * ,  (18)

n = 0

где m = 0,1,., N -1.

Замечание 4.1. При интерпретации редуцированных кодов как битовых представлений элементов поля классов вычетов по модулю f простого числа Ферма введенное шифт-преобразование совпадает с ТЧП Ферма при ш = 2 (mod f ). В этом случае при m Ф k (mod 2B) равенство

T - 1

^ 3^-rnk <3^ < E > * > * n = 0

равносильно очевидному равенству

2 B - 1

0 . £ 2 ^{n ( m - k} ) (mod f ).     (20)

n = 0

При m = k (mod 2 B ) значение сумм (19) и (20) равны 2B (mod f). В общем случае шифт-преобразований значение суммы (19) определяется конкретной интерпретацией действий над кодами, связанной с арифметическими операциями в ассоциированном конечном кольце.

Лемма 4.2. Пусть < E > • = (0, 0,., 0, 1), T = 2 B есть период последовательности

SSS

<3n E > . Тогда для колец K = Sp, Sq , /r при m Ф k (mod 2B) справедливо соотношение (19). При m = k (mod 2B) значение суммы (19) равно 2B (mod p), (mod q), (mod r), соот ветственно.

Доказательство. Если рассматривать соотношение (17) как преобразование, инду цированное умножениями на элементы

(V 2 ) ,

y ( 3 2 ) и у ( з/2 )

соответственно, то единствен ной причиной нарушения равенства (19) мо жет служить, например, для кольца

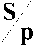
нео-

братимость элементов

( 3 2 V - 1 = ( 3 2 ) Г -1 при суммировании членов геометрической прогрессии. Этого не

_                мI ЗА происходит, если Normy^ I \v2 / 1 есть число, взаимно простое с f.

Но при т Ф 0 (mod 3) имеем

NormyY х х^(3/2)с-1 J=^(3/2f- 1р(3/2)с- 1р(3/2 Г-1^= 2т-1.

При т = 0 (mod 3 ) имеем

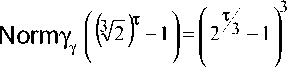
и существование нетривиального общего де лителя чисел Normy^v 32) - 1J невозможно при и = 0, 1, 2 и т > 3. При т = 1, 2, 3

((3R элементы I v 22-)  1 являются единица- ми кольца S и, следовательно, обратимы в соответствующих фактор-кольцах.

Лемма 4.2 позволяет рассматривать “правое” шифт-преобразование как обратное по отношению к “левому” шифт преобразованию (18) и наоборот.

Вычисление свертки

Рассмотренные выше шифт-преобразо-вания позволяют вычислять циклическую свертку целочисленных 2 B- периодических последовательностей c помощью ( B+1) -битовых процессоров по обычной спектральной схеме (см., например , [16]). Опуская детали описания такой схемы, сформулируем окончательный результат.

Теорема. Если для числа Ферма (8) выполняются условия (а)-(с),то для вычисления циклической свертки длины N = 2(3 t + 1) достаточно выполнения:

• 1.    девяти (шести левых и трех обратных) шифт-преобразований;

• 2.    вычисления произведений компонентов спектров шифт-преобразований;

• 3.    реконструкции значений свертки по китайской теореме об остатках в форме (12).

Если число Ферма имеет вид f = 2 B +1, B = 2r = 3t -1 и обладает свойствами:

• (d)    при всех 1 < s <  3t -1 числаf и 2 ⁵ -1 взаимно просты ;

• (e)    элемент 2(31 -1) обратим в фактор-

• кольце

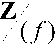
• (f)    число f не делится на 3 , то есть f Ф 0 (mod 3),

то достаточно рассмотреть разложение числа f на множители в кольце S целых элементов поля разложения полинома ^ ( z ) = 2 z ³ + 1 над Q .

В S для числа f наряду с представлением в виде произведения целых рациональных чисел возможно представление в форме, аналогичной ( 9 ):

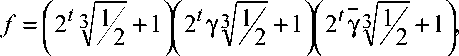
где у - примитивный корень третьей степени из единицы. Как и в лемме 3.1, доказывается взаимная простота элементов

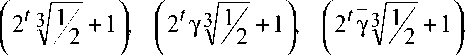
Доказательства аналогов соответствую щих лемм и теоремы также существенно не отличаются от приведенных выше.

Непосредственная численная проверка показывает, что числа Ферма f , f , f удовлетворяют условиям ( a ) -(c) или (d)-(f), что позволяет вычислять свертки длин 64, 128, 256 с помощью описанного метода.

Заключение

Возможности рассмотренного метода, по мнению автора, не ограничиваются задачей «безошибочного» вычисления свертки. Представляется перспективным его использование, например, при быстром параллельном возведении в степень в конечных полях (массовая криптографическая задача), при сжатии информации и т.п.

В этой связи основную техническую трудность при обобщении на случай иррациональностей высших порядков представляет отыскание явного вида вложения кольца вычетов (mod f в прямую сумму колец (лемма 3 .2).

Экстраполяция результатов на случай модулейp более общего видаp = bk ± 1 также не вызывает принципиальных затруднений. В [19] приведены разложения чиселp на простые множители. Практическая целесообразность такого обобщения ограничивается ис- ключительно возможностями вычислительных средств, ориентированных на недвоичное представление информации [10].