Синтез параметров системы на базе метода молекулярной динамики для моделирования газовой фазы в замкнутом нанообъеме

Выбор конфигурации системы является одним из самых важных этапов постановки численного эксперимента (ЧЭ). Параметры и допущения принятые во время разработки явным образом влияют на конечный результат вычислений и должны соответствовать поставленной задаче [1].

В данной работе на первое место ставится удобство сравнения результатов моделирования с известными из литературы данными. Для выполнения данного условия, были приняты следующие допущения:

• •    Система замкнутая с фиксированным кол-вом частиц

• •    Геометрически представлена параллелепипедом

• •    Все поверхности атомарно-гладкие

• •    Все, кроме одной, ограничивающие поверхности адиабатические и непроницаемые для частиц (упруго отражающие) [2]

• •    Одна поверхность адсорбирующая и осуществляющая теплообмен (обладает бесконечной теплоемкостью)

• •    В объеме отсутствует вещество, помимо пробы

• •    Все частицы (как газа, так и стенки) сферические

• •    Не рассматривается вращение и поляризация частиц

• •    Между собой частицы газа взаимодействуют по ПЛД6-12 [1, 3]

• •    Частицы газа взаимодействуют с частицами адсорбирующей поверхности по ПЛД5-10

Такая конфигурация делает синтезированную систему близкой по свойствам к описываемым теорией полимолекулярной адсорбции Брунауэра-Эммета-Теллера [4].

Следующим этапом в создании модели, стало проведение оценки вычислительной мощности имеющихся в доступе ЭВМ. Данное действие было направлено на выбор максимального кол-ва частиц в эксперименте, при котором время проведения одного опыта не превышало бы 20-25 минут. Был составлен синтетический тест времени выполнения алгоритмов для различного кол-ва частиц, результаты которого приведены на рисунках 1–3.

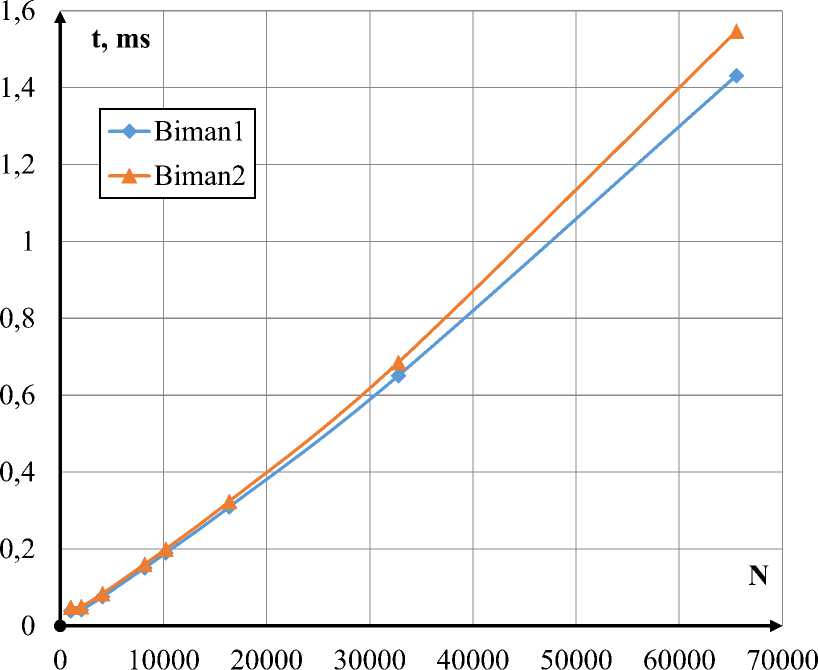
Рисунок 1 – Время выполнения алгоритма Бимана

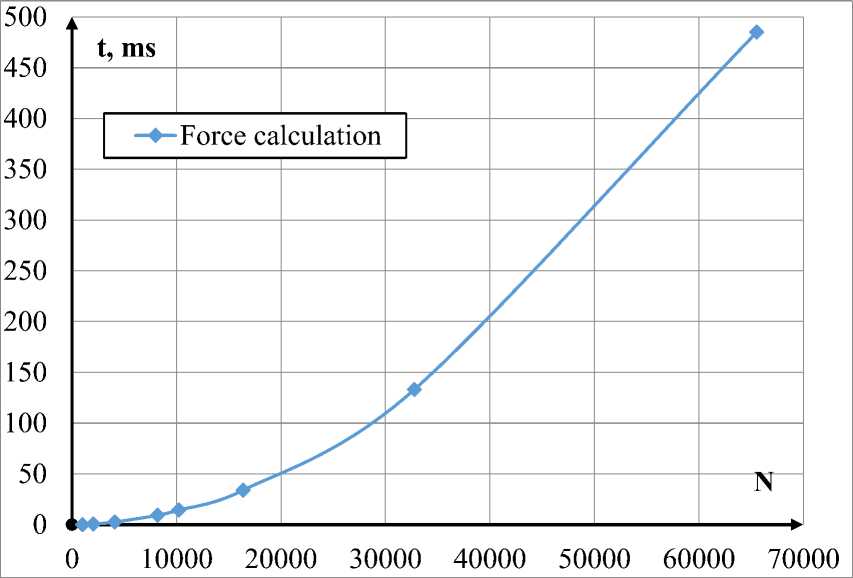
Рисунок 2 – Время выполнения расчета межмолекулярных сил

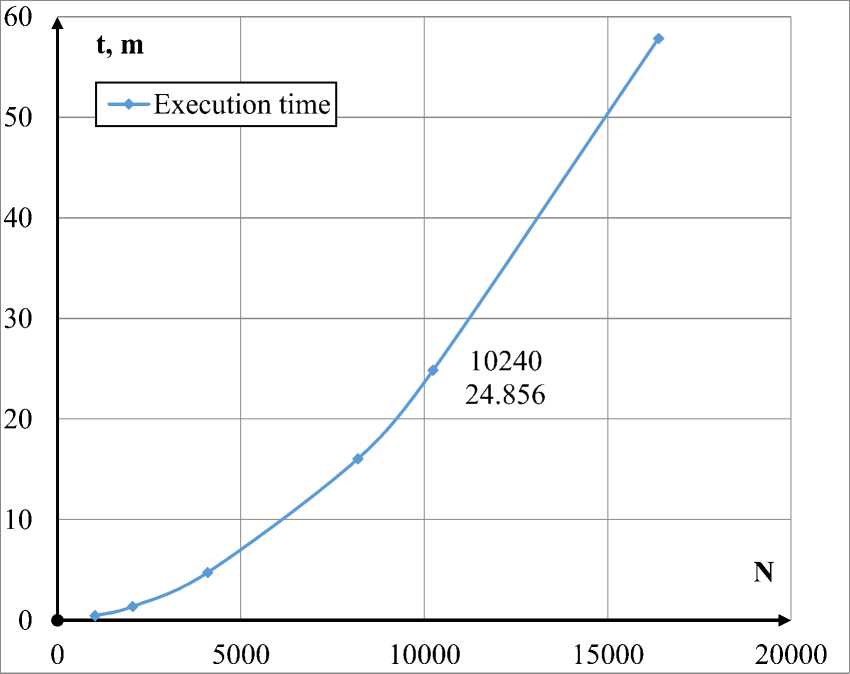
Рисунок 3 – Время выполнения10^5 итераций

Из рисунка 3 видно, что при кол-ве частиц равном 10240, время выполнения ЧЭ близко к 25 минутам, что удовлетворяет сформулированному ранее условию.

Исходя из полученного ранее кол-ва частиц, можно рассчитать геометрические размеры системы. Запишем уравнение Менделеева-Клапейрона:

PV = nRT = NRT

Na

V =

N Nap

RT

Т.к. все значения правой части теперь известны, рассчитаем объем:

_ 10240 *8.3145 T

_ T = 1.4138 * 10 ^-19-

V = 6.0221 * 1023 *P

L_n~W = 5.2095 * 10 ^-7

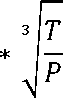
Положим L_x = L y = L = 4.5 * 10 ⁸ м. Тогда длина оставшейся грани L_z будет рассчитываться исходя из требуемых параметров T и P (температура и давление).