Синтез ПИД-регулятора для объектов второго порядка с учетом расположения полюсов

Синтез регуляторов систем автоматического управления (САУ) – одна из основных предметных задач теории автоматического управления. Наибольшее распространение в САУ технологическими процессами получили пропорционально-интегрально-дифференцирующие (ПИД) регуляторы [1]. Одним из методов синтеза ПИД-регуляторов [2], активно развиваемым учеными, выступает модальный метод [3, 4 и др.]. В научных работах, посвященных синтезу регуляторов, отсутствуют соотношения, связывающие значения переходной характеристики и коэффициентов объекта управления с учетом расположения комплексных полюсов.

Наиболее распространенными для мобильных строительных и дорожных машин как объектов управления являются математические модели второго порядка.

Исходное математическое описание системы и постановка задачи

Рассматривается линейная система автоматического управления с передаточной функцией (ПФ) объекта второго порядка.

Передаточная функция объекта управления второго порядка W o ( s ) и ПИД-регулятора W y ( s ) имеет вид

W o ( 5 ) =

b 0 ⁵ + b l      .

a ₀ 5 ² + a 1 s + a ₂ ’

K,s ² + K s + K dpi

s

Wy (5) = Kp + K + KdS = s где s – преобразователь Лапласа; Kp, Ki, Kd – соответственно коэффициенты пропорциональности, интегрирования и дифференцирования.

При последовательном соединении ПФ объекта и ПИД-регулятора образуют разомкнутую систему с ПФ следующего вида:

W ( 5 ) = W o ( 5 ) W y ( 5 ) =

K d b ₀ 5 ³ + ( кд + K p b ₀) 5 ² + ( кд + K p b ) 5 + Kb

3         2

a ₀ 5 + a 5 + a ₂ 5

ПФ замкнутой системы управления с единичной обратной связью

W ( 5 ) =        K d b 0 ^ ^{3 +}1 K d b ⁺ K p b 0 ) ^ ^{2 +} I K i b 0 ⁺ K p b ) ^ ⁺ K i b

1 + W ( 5 ) ( a 0 + K d b o ) 5 ³ + ( a , + K d b + K p b o ) 5 ² + ( a 2 + K i b 0 + K p b)5 + K i b '

Исходными данными для синтеза ПИД-регулятора САУ являются ПФ объекта управления W_o ( s ) второго порядка и заданные показатели качества: перерегулирование и время регулирования.

Решается задача определения значений коэффициентов ПИД-регулятора K_d , K_p , K_i , обеспечивающих заданные показатели качества по заданным ПФ объекта управления второго порядка W_o ( s ) и значениям действительного полюса s ₁ = –η₁ и комплексных полюсов s ₂ = –η₂ + j β; s 3 = –η 2 – j β ПФ замкнутой системы управления.

Вывод основных соотношений

ПФ замкнутой системы с ПИД-регулятором при задании комплексных полюсов представим в виде

к₍ ) - W ( s ) - Kb 0 s ³ + ( K d b * + Ws ² + ( Kb 0 + K p b i )^{S + K}b ^S   1 ⁺ W ^{( s} )     ⁽ a 0 ⁺ K d b ₀)( ^{s +} П 1 ^{)( s +} П 2 ^{+ e} j ^{)( s +} П 2 ^{- e} j )

Введем обозначения для упрощения выражения (1):

K d b 0      - K ' K p b .     - K i b 0 ⁺ Kb к - Kb

TZ 1 ; b01                        ; b02             ,z 7    ; b03            TZ 7 - a 0 + Kdb0       a 0 + Kdb0        a 0 + Kdb0       a 0 + Kdb0

С учетом выражений (2) получим в области изображений для переходной характеристики замкнутой системы с ПИД-регулятором при задании значений комплексных полюсов:

h ( s ) =

^b 00 ^{s 3 + b} 01 ^{s 2 + b} 02 5 ^{+ b} 03

⁽ s ⁺ П 1 ⁾⁽ s ⁺ П 2 ^{+ e} j ⁾⁽ s ⁺ П 2 ^{- e} j ) s"

Характеристическое уравнение замкнутой системы имеет третий порядок. При известных заданных действительном полюсе s ₁ и комплексных полюсах s ₂, s ₃

Si     ii; ^ 2     ic+ e j; 5 3     ic- e j, это уравнение имеет вид

Д < _s ) = : _s - ^ .x ^ - ^ , )( _s - _s 3 ) = ^ - + 01, + 2л , )Г + [, , (, , - ...■ +(П з ^{+ e} 7 ')+ П2 ^-РУ)]s + П,⁽П ^-₽7⁾⁽П2 + ^ej).

Применим упрощение

П 1 (П 2 ^{- e} j )+(П 2 ^{+ e} j )(П 1 ⁺ П 2 ^{- e} j )] = ^e2+n i ^{+ 2}П 1 П 2 , П 1 (П₂ - в j )(n₂ + в j ) = П 1 (в²+П 2 ) -

Тогда характеристическое уравнение примет следующий вид:

D ( 5 ) = 5 ³ + (П ] + 2n₂) 5 ² + Ф² +П 2 + ²п П 2 ) ^{5 +} П 1Ф² +п 2 ).

Характеристическое уравнение корректируемой системы можно представить таким вы-

ражением:

( a 0 + K d b 0 ) 5 ³ + ( a ! + K d b ! + K p b 0 ) 5 ² + ( a 2 + K i b 0 + ^K p ^b 1 ) 5 + K i b !

a 0 ⁺ K d b 0

= 5 3 +

Г a i + K d b ! + K p b 0 ) ₂

5 +

I    a 0 ⁺ K d b 0    J

Г a 2 + Kb + K p b ) , Kb

5 +

(    a 0 + K d b 0    J    a 0 + K d b ₀

-

Приравнивая коэффициенты при одинаковых степенях s , получим:

a i + K d b i + K p b о

------„ , p = П 1 + 2П 2 ;

a 0 ⁺ K d b 0

a ₂ + Kb + Kh   ₇ ,

²     ‘ ° ,p ¹ = в²+п 2 + ²nn 2 ;

a ° + K d b °

Kb   = ni(e2+n2)- a 0 + Kdb0

Определим установившееся значение h stab переходной характеристики h ( t ) при задании комплексных полюсов в соответствии с теоремой предельного перехода:

lim( s • h ( s )) ^

⁵ ^ 0

Kb

П 1 ⁽П 2 ^{- e} j ⁾⁽П 2 ^{+ e} j ⁾⁽ a 0 ⁺ K d b o ) ’

тогда установившееся значение h_stab

h = stab.

Kb

П 1 ⁽П ^{- e} j )(П 2 + ^e j ⁾⁽ a 0 + K d b o )

-

Упростив выражение (5), получим

Kb hsab’ -.       .a + Kdb0)

.

В соответствии с (4)

-ib¹!^;" = n i (n 2 +e²), a 0 ^{+ 1}d^b 0

подставляя (7) в (6), имеем

h flstab.

K i b 1

_ П 1 (П 2 +в²)

П 1 ⁽п 2 ^+в 2 ⁾⁽ а о ⁺ K d b о ) П 1 ⁽П 2 ^+в2)

= 1.

Полученный результат (8) подтверждает, что рассматриваемая замкнутая система управления является астатической относительно входного воздействия.

Определим начальное значение h переходной характеристики h ( t ) в соответствии с тео- sta .

ремой предельного перехода для случая задания комплексных полюсов:

т. е

li^m( s • h (s )) ^

s ^^

K_db ₀ a 0 + K_db о ,

^h init .

K d b 0 a о + K d b о

.

Доказано, что для рассматриваемой задачи синтеза ПИД-регулятора системы управления с ОУ второго порядка справедливо условие h_init. ≤ h ( t ) ≤ 1 при установившемся значении h_stab. = 1. Это выражение не зависит от типа заданных полюсов.

Таким образом, значение переходной характеристики замкнутой системы с ПИД-регулятором изменяется во времени от h init. до h stab. = 1. При этом если значение b 0 = 0, то начальное значение переходной характеристики h_init. = 0. ^.

Очевидно, что при некотором значении b 0 , h init. войдет в 5%-ю зону установившегося значения. Это свидетельствует о возможности значительного уменьшения времени переходного процесса при b 0 не равного 0.

Определение значений составляющих переходной характеристики замкнутой системы управления

Определим составляющие переходной характеристики h ( t ) замкнутой системы с ПИД-регулятором в соответствии с теоремой предельного перехода, при задании комплексных полюсов в среде программы MathCAD применив функцию упрощения (simplify):

lim [ ( ⁵ + П 1 ) h ^{( 5} ) ] simplify

⁵ ^-Tl,

(b, -ЬоП1)(Kd n2 -Kp n,+Ki);

П1 (ao+Kd Ьо)(в2 + П2 -2П,П + П2) ’ lim [(5 + n + в j) h (5)] simplify ^

• ⁵    >  - - j

  - (ЬоП2 - bl + вb0 j)(Kd n2 - Kp в j - Kd в2- Kpn + 2KdPn2 j) j 2Р(П2 + в j)(ao+Kdbо)(п2 -П1 + в j)’

lim [ ( 5 + p₂ - в j ) h ( 5 ) ] simplify ^

( b , - b 0 П 2 + в b 0 j )( K d n 2 - 2 jK d вП 2 - K d в² - K p П 2 + K i +K p в j ) j

.

^{2 в(}П 2 ^{- в j )(} a 0 ^{+ K}d b 0 ⁾⁽П 1 ^- П 2 ^{+ в j} )

Обозначим:

установившееся значение h stab. в соответствии с (6)

h sab .

K i b 1

П 1 (п 2 +в²)( a 0 + K d b o )’

при подстановке исходных данных получим установившееся значение hstab. переходной характеристики hstab. = 1, тогда составляющая hs (t) обусловленная полюсом s1 = –η1, h (t) = _ (b - b0П1)(Kdn2 - Kpn + K) _ e_n^ s1        П1(a0 + Kdb0)(в2 + П2 - 2П1П2 + n2)

составляющая hs (t), обусловленная комплексным полюсом s2 = –η2 + jβ, hs 2( t) = -

• (b0П2 - b + ebo j)(Kd П2 — Kpe j - Kde 2-KpП2 + 2Kdj)j. e(_Л2-в»t(10)

2Р(П2 + в j)(ao+KdboXn -П1 + в j)

составляющая hs (t), обусловленная комплексным полюсом s3 = –η2 + jβ, h (t) = (b -b0П2 + вb0 j)(Kd n2 - 2 jKd К - Kd в2 - KpП2 + K +Kp в j) j e(-П2 +ej)t

$3                     2в(П2 -в j)(a0+Kdbо)(П1 -П2 + в j)               6. ()

Таким образом, для комплексных полюсов выражение переходной характеристики h ( t ) примет следующий вид:

h ( t ) = h stab + h s , ( t ) + h s, ( t ) + h s, ( t ),                                                       (12)

или, упростив выражение (12), заменив сумму h s ( t ) + h s ( t ) на удвоенную действительную часть 2Re [ h „( t ) ] или ^2Re [ h„⁽t ) ] , т. е

h ( t ) = h_sto b + h 1 ( t ) + 2 Re [ h s ₂ ( t ) ] , или h ( t ) = h sab + h 1 ( t ) + 2 Re [ h s 3 ( t ) ] -

Графическая реализация проверки примененного упрощения представлена на рис. 1: приня^тые обозначения M t ) = ^2Re ^[ h s ₂ ⁽ t ) ] или h _B ⁽ t ) = ^2Re ^[ h s з ⁽ t ) ] .

Синтез параметров пид-регулятора

Равенства (4) представим в виде системы уравнений, в которой неизвестными являются значения коэффициентов ПИД-регулятора

K d [ b - b ₀(n . + 2n₂)] + K p b 0 = a о (П 1 + 2n₂) — <4;

• - Kb о ( в² +n 2 + 2П 1 П 2 ) + K p b i + Kb 0 = a о (в 2 +п 2 + 2П 1 П 2 ) — a 2 ;             (¹³)

— ^K d ^b 0 ^П 1 ^{(в +n} 2 ) ^{+ K} i ^b 1 = a 0 ^П 1 ^{(в +П} 2 )-

Введем обозначения для представления системы уравнений в матричной форме:

^ ii = ^b 1 — ^b ohi ^{+ 2п} г ); ^ 12 = ^b о ^; ^ 13 = ^{0; с} 1 = a ohi ^{+ 2п} г ) ^- a i ^;

• ^ 21 =- b о ( в²+П 2 + 2n i П 2 ) ; ^ 22 = b i ; ^ 23 = b о ; с 2 = а о (в²+п 2 + 2n i П 2 ) - а 2 ;   ⁽¹⁴⁾

^ 3i =- b o n i (e²+n 2 ); ^ 32 = 0; Х 33 = b i ; с з = a o n i (e²+n 2 )-

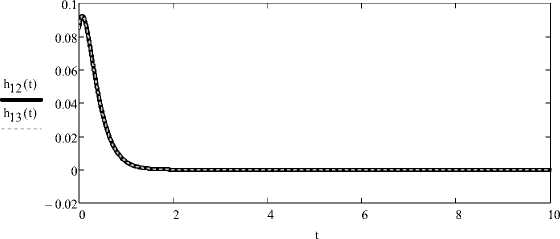
Рис. 1. Графическая реализация упрощения замены суммы hs (t) + hs (t) на удвоенную действительную часть 2 Re [hs (t)] или 2Re [hs (t)]

С учетом принятых обозначений (14) сформируем матрицы:

	' A i	A 2	A 13 )		' c 1 )		f K d
Л =	^ 21	^ 22	A 23	c = ’ c 2	с 2	; К 2 =	kp	.                                        (15)
	1 A 31	A 32	A 33 ;		v с 3 )		V K i )

Матричное уравнение для определения искомых значений коэффициентов регулятора

имеет вид

( A- K 2) = C 2.

А его решение представляется в виде

	K 2 =Л С 2'
Система	уравнений (13) значительно упрощается, если значение коэффициента
b 0 = 0:	a . + Kb —1— d-1 = n 1 + 2n 2 ;

a ₂ + Kb , ,

-—p -^ = e ² +n 2 + 2П 1 П 2 ;

a ₀

Kb = nX+n 2 )- a ₀

В этом случае уравнения для расчета значений коэффициентов ПИД-регулятора имеют вид

= c = a 0 ⁽П 1 ⁺ 2П 2 ) ^- a l _; b ₁ b ₁

- = c. = a 0 (0 2 +4 2 ⁺ 2П 1 П 2 ) ^- a 2 _; ^p b 1 b 1

K = C 3 = a о П 1 (в 2 +п 2 ) b i .

ⁱ b ₁ b ₁

Получены выражения для расчета коэффициентов ПИД-регулятора, включающие коэффициенты ПФ объекта второго порядка при заданных значениях комплексных полюсов. Выполнена проверка рассмотренной методики на конкретном примере.

Пример. Задан объект управления второго порядка с ПФ

W o ( S ) =

b0 s + bl a 0 s 2 + a1 s + a 2

0,01 ^ ⁺ 0,7 0,04 s ² + 0,12 s + 1

Требуется синтезировать ПИД-регулятор, который обеспечит переходную характеристику без перерегулирования, а время регулирования t p = 3 c.

Для реализации метода синтеза применены зависимости (15), (17). Расчеты выполнены в среде программы MathCAD.

Исходные данные для комплексных значений полюсов:

значение η 1 определено с учетом желаемого времени регулирования, равного 3, с и расчета по известной приближенной формуле [5, 6]

t _р

3 _, Re( s )

П 1 = Re( 5 ),

где Re( s ) – действительная часть полюса, наиболее приближенного к мнимой оси корневой плоскости; значение η 2 и β определяется из требуемого значения перерегулирования и влияния этого полюса на полюс η₁

П = 1;П 2 = 5; в = 0,5; b = 0,7; b ₀ = 0,01; a 0 = 0,04; a , = 0,12; a 2 = 1,0.

Для заданных комплексных полюсов определены коэффициенты ПИД-регулятора:

Г кА

К 2 =

K

VKi 7

Г 0,528 А 0,828 ( 1,633 7

; К. = 0,528; К = 0,828; К = 1,633. dpi

Выполнено моделирование переходного процесса для периода времени t = 0,0.001…10.

Cоставляющие h s 1 ( t ), h s 2 ( t ), h s 3 ( t ), обусловленные полюсом s 1 = –η 1 и комплексными полюсами s 2 = –η 2 + β j ; s 3 = –η 2 + β j , определяются по зависимостям (9) – (11).

Переходная характеристика h ( t ) получена по выражению (12). При t = 1 получим h ( t ) = h_sto b + h. ( t ) + h r , ( t ) + h r , ( t ) = ^0,117 .

Начальное значение h init. переходной характеристики h ( t )

h init.

K d b 0 — ^a 0 ⁺ K d b 0

= 0,117.

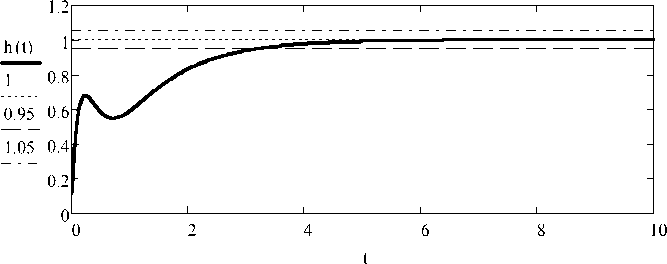
Рис. 2. График переходного процесса синтезированной системы с заданными комплексными полюсами t p = 3 c при b 0 = 0,01

На рис. 2 представлен график переходного процесса h ( t ) замкнутой САУ с синтезированными параметрами ПИД-регулятора.

При известном значении b ₀ = 0,01, заданных параметрах объекта второго порядка и комплексных полюсов в рассмотренном примере время переходного процесса, исходя из условия 5 % зоны установившегося значения, равно 3 с.

Определены коэффициенты ПИД-регулятора при b 0 = 0,05:

К 2 =

K p

V \ 7

< 1,098 )

3,106

3,423

; K d = 1,098; K p = 3,106; K_i = 3,423.

Начальное значение h_init. = 0,579 переходной характеристики h ( t ) при b ₀ = 0,05. ^.

На рис. 3 представлен график переходного процесса h ( t ) замкнутой САУ с синтезированными параметрами ПИД-регулятора при значении коэффициента объекта b ₀ = 0,05.

При известном значении b0 = 0,05, заданных параметрах объекта второго порядка и ком- плексных полюсов в рассмотренном примере время переходного процесса, исходя из условия 5 % зоны установившегося значения, равно 2,45 с.

Определены коэффициенты ПИД-регулятора при b ₀ = 0,1:

К 2 =

(к- А d

K p

V Ki 7

( 5,420 "  24,878

V 20,992 7

; K d = 5,420; K p = 24,878; K i = 20,992.

Начальное значение h init. = 0,93 переходной характеристики h ( t ) при b 0 = 0,1

На рис. 4 представлен график переходного процесса h ( t ) замкнутой САУ с синтезированными параметрами ПИД-регулятора при значении коэффициента объекта b 0 = 0,1.

В соответствии с разработанной методикой модального синтеза ПИД-регулятора для объ- ектов второго порядка переходный процесс носит апериодический характер. При известном значении b0 = 0,1, заданных параметрах объекта второго порядка и комплексных полюсов в рассмотренном примере время переходного процесса, исходя из условия 5 % зоны установившегося значения, равно 0 с.

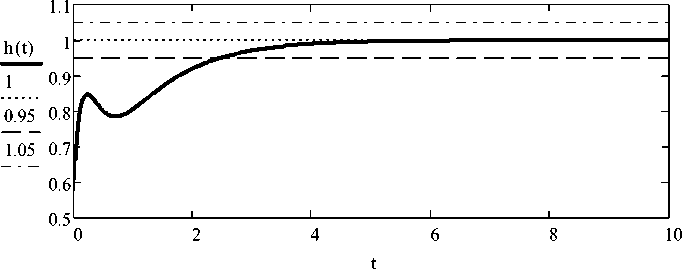
Рис. 3. График переходного процесса синтезированной системы с заданными комплексными полюсами t p = 2,45 c при b 0 = 0,05

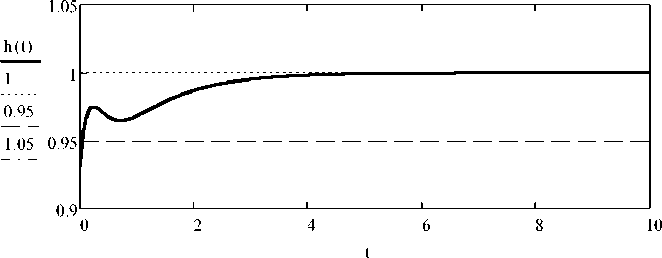
Рис. 4. График переходного процесса синтезированной системы с заданными комплексными полюсами t p = 0 c при b 0 = 0,1

Определение коэффициента b 0 передаточной функции объекта по заданному начальному значению h init. переходной характеристики h ( t )

Преобразовав зависимость (18), получим следующее выражение для расчета b 0 ( h init. ) :

^b 0 ^{( h} init . ⁾

I 1

a ₀

, K d =

h init .

- 1 | K d

a 0 ⁽П 1 + 2П 2 ) — a l b ₁

тогда итоговая зависимость примет вид b (h™,) = — 7-------.                                   (19)

n .

I 1

I          ¹ |[ a l ^- a 0 ⁽П 1 + 2П 2 ) ]

v h init.     ;

При заданном начальном значении переходной характеристики h init. = 0,95 величина коэффициента равна b 0 ( h init. ) = 1,6625.

Зависимость (19) позволяет выполнить расчет коэффициента b передаточной функции объекта по заданному начальному значению h_init. переходной характеристики h ( t ), коэффициентов ПФ объекта ( b 1 , a 0 , a 1 ), заданных полюсов (η 1 , η 2 ) системы управления. Рекомендации по определению значений комплексных полюсов могут быть предложены после дополнительных исследований по разработанной методике.

Заключение

Разработана методика модального синтеза ПИД-регулятора по заданным значениям параметров объекта второго порядка и комплексных полюсов замкнутой системы управления.

Исследование показало, что при некотором значении b ₀, не равного 0, начальное значение переходной характеристики h init. войдет в 5%-ю зону установившегося значения. Это свидетельствует о возможности значительного увеличения быстродействия скорректированной системы.