Синтез полиномиальных регуляторов заданной точности для неминимально-фазовых объектов

Введение. В современной теории автоматического управления существует большое количество методов синтеза регуляторов. Некоторые из них концептуально просты, однако их использование ограничивается отсутствием четких рекомендаций относительно применения этих методов для конкретных объектов и требований к их качеству. К числу таких методов относятся методы синтеза компенсационных регуляторов [1], с использованием которых в рамках общего подхода для одного объекта может быть получено несколько регуляторов различных порядков. Все эти регуляторы основаны на идеях метода желаемой передаточной функции, в соответствии с которыми нули и полюсы системы размещаются в заданных точках комплексной плоскости. В данной работе рассматривается возможность обеспечения регулятора дополнительными свойствами, в частности обеспечения заданного уровня установившейся статической ошибки.

Описание метода желаемой передаточной функции. Идея синтеза регулятора методом желаемой передаточной функции состоит в том, что для известной передаточной функции объекта

= Р^ ) = P m S m + P m - 1 S m ' + ... + Р 0

^{R (} s )       r_ns " + r_n - 1 s " ^{- 1} + ... + ^r 0

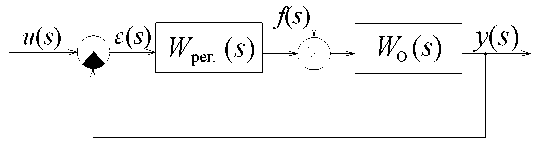
Рис. 1. Структурная схема системы управления '

и желаемой передаточной функции замкнутой системы по управлению W _к( 5 ) для структурной схемы, представленной на рис. 1, можно записать

W W^ = w ( ^ )

1 + WЛ 5 )W,(5 )   ж где Wрег(5) - искомая передаточная функция регулятора. Разрешив это равенство относительно Wрег(5), получаем

W _{pe Г}( 5 ) = —-- ^W^ ⁵ )

'      W Д 5 )1 _ W Д 5 )

Данный подход хорошо известен, однако его непосредственное применение для неминимально-фазовых объектов приводит к физически не реализуемой или негрубой системе, так как регулятор, полученный по формуле (2), содержит в качестве сомножителя величину, обратную передаточной функции объекта, что приводит к сокращению нулей и полюсов, в том числе правых. Компенсация левых полюсов не нарушает устойчивости объекта, однако может вызывать скрытые колебания координат, которые часто нежелательны, так как приводят к дополнительному расходу энергии управления и увеличению динамических нагрузок в силовой части системы.

Получить работоспособную систему можно, наложив ряд ограничений на структуру желаемой передаточной функции замкнутой системы W _к( 5 ) и передаточную функцию регулятора W х;г( 5 ) [2, 3]. В частности, можно потребовать, чтобы функция W _к( 5 ) была представима в виде

W - ⁽ 5 ) = Т ТЛ M ( 5 ), G ^{( 5} )

где G ( s ) - характеристический полином желаемой передаточной функции; M ( 5 ) = m_k5^k + m_k _ 1 5^{k _ 1} + ... + m ₀ - полином, подлежащий определению. При выполнении данного условия передаточная функция регулятора не будет содержать нулей, сокращающихся с нулями объекта.

Для того чтобы функция W _рег( 5 ) не содержала полюсов, сокращающихся с нулями объекта, необходимо выполнение условия

1 " W . ( 5 ) = R T ⁵ ; N ( 5 ), G ( 5 )

где полином N(5) = nt5* + nt_1 51 _1 +... + n0 также подлежит определению. Из (3) и (4) следует w (5) = MM рег(      N (5) ■

Для вычисления коэффициентов полиномов N ( 5 ) и M ( 5 ) необходимо выполнить подстановку (3) в (4), в результате чего получаем полиномиальное уравнение

P ( 5 ) M ( 5 ) + R ( 5 ) N ( 5 ) = G ( 5 ) ,

из которого может быть сформирована система уравнений относительно коэффициентов искомых полиномов N ( s ) и M ( s ) .

Выбор порядков полиномов G ( s ), N ( s ), M ( s ) зависит от условий разрешимости, физической осуществимости и грубости [3], которые могут быть записаны в виде системы неравенств относительно степеней полиномов рассматриваемых передаточных функций.

Будем использовать величину nG для обозначения порядка полинома G(s). Так как число уравнений относительно коэффициентов, получаемых из (5), равно nG +1, а число неизвестных равно nM + nN + 2, для разрешимости системы должно выполняться неравенство nG ^ ПМ + nN + 1                                     (7)

Для выполнения условия грубости необходимо, чтобы относительный порядок передаточной функции регулятора был неотрицательным. Очевидно, что это условие выполняется, если nM ^ nN + r ,                                            (8)

где r - необходимый порядок астатизма синтезируемой системы.

Относительный порядок передаточной функции в левой части (4) равен нулю. Следовательно, относительный порядок передаточной функции в правой части (4) также должен быть равен нулю. Таким образом:

n G = n R + n N ^{+ r} .                                           ⁽⁹⁾

Естественным ограничением является также условие правильности передаточной функции желаемой системы nG > Пр + Um + r ,                                       (10)

Выражения (7)-(10) учитываются при определении степеней неопределенных полиномов M(s) и N(s), в качестве которых обычно рекомендуется выбирать минимально возможные степени. Из этих выражений также можно определить ограничения снизу на порядок желаемой передаточной функции системы nG nG > 2nR - 1.                                           (11)

Очевидно, что при использовании такого подхода невозможно обеспечить произвольную функцию W _к( s ), т. е. произвольное расположение ее полюсов и нулей. Обычно задается лишь расположение полюсов исходя из требований к динамическим характеристикам замкнутой системы и ее астатизму. Вместе с тем метод позволяет частично управлять нулями замкнутой системы, которую можно использовать для получения наилучшего или заданного качества.

Постановка задачи. Из соотношений (7)-(10) следует, что выбор полиномов G ( s ), N ( s ), M ( s ), а следовательно, и W _рег( s ) не является однозначным. Эта неоднозначность может быть использована для обеспечения выполнения дополнительных требований к замкнутой системе, одним из которых является статическая точность. Известно, что одним из способов повышения статической точности является введение астатизма. Однако при использовании этого метода уменьшается запас устойчивости и снижается быстродействие. Другим вариантом является обеспечение заданного уровня статической ошибки регулирования.

В предположении, что передаточная функция регулятора определяется отношением (5), установившаяся ошибка £_т для схемы на рис. 1 может быть записана в виде

1         Р о / ^Г 0 У

£ =--- U + —--⁰ f , ОО 1      7     00       1      7 V СО "

• 1    + к 1 + к

где k = ( m ₀ /п ₀ )( p ₀/ г ₀ ) . При фиксированных p ₀ и r ₀ увеличение коэффициента усиления разомкнутой системы и соответственно уменьшение г_т при сохранении желаемого характеристического полинома G ( 5 ) возможно только тогда, когда имеется возможность варьировать коэффициенты п ₀ и m ₀. Для этого необходимо, чтобы уравнение синтеза (6) было недоопределено, т. е. число неизвестных было больше числа уравнений.

Пусть объект управления описывается передаточной функцией (1). В соответствии с (11) минимальный порядок желаемого полинома nG = 2п -1 и число уравнений, которые можно получить на основе (6), равно 2п. В соответствии с (9) размерность полинома N(5) равна nN = п -1. Соответственно число неизвестных коэффициентов равно nt - п. Максимальная размерность полинома M(5), соответствующая реализуемому интегродифференцирующему регулятору, согласно (5) равна пм = nN = п-1, а число неизвестных коэффициентов mt равно п . Полученная система уравнений относительно пр mt имеет единственное решение и не позволяет регулировать уровень статической ошибки замкнутой системы. Таким образом, возможность подстройки статической ошибки требует более высоких порядков полиномов G(5), N(5), M(5), чем те минимальные значения, которые следуют из (7)-(10).

Рассмотрим возможности обеспечения дополнительной точности и грубости компенсационного полиномиального регулятора на примере расчета регулятора для неустойчивого объекта - перевернутого маятника, описываемого дифференциальным уравнением

■ ■

Ф = —дф + — и .

• 2    L     2 L

Здесь L - длина маятника; ф - угол отклонения маятника от вертикали; и - управляющее воздействие. Объект является структурно-неустойчивым, так как характеристическое уравнение имеет два вещественных корня - положительный и отрицательный.

Передаточная функция объекта по управлению имеет вид

W ( 5 ) = P⁵ ) = -у¹⁶— .

R ( 5 )    5 ² - 16

В соответствии с (11) минимальный порядок желаемого полинома G ( s ) равен 3. Примем G ( 5 ) = ( 5 + 10) ³ = 5 ³ + 30 5 ² + 3 00 5 + 1000.

В данном случае из (3) следует N ( 5 ) = п 1 5 + п ₀. Соответственно полином M ( 5 ) должен быть не выше первого порядка. Из условия разрешимости следует M ( 5 ) = m 1 5 + m ₀.

Условия (2), (3) имеют вид

W _к( 5 ) =

--^^ M ( 5 ) , 1 - W _K ( 5 ) =  -- N ( 5 ) , ( 5 + 10) 3                ^Ж      ( 5 + 10) 3

а уравнение синтеза -

16 M ( 5 ) + ( 5 ² - 16) N ( 5 ) = 5 ³ + 30 5 ² + 3 00 5 + 1000.                       (13)

Подставляя N(5) и M(5) в (13) и приравнивая коэффициенты при одинаковых степенях s , по лучаем систему уравнений п1 = 1, n0 = 30, 16m 1 -16n1 = 300, 16m0 -16n0 = 1000.

Отсюда следует m 1 = 19,75, m0 = 92,5, n1 = 1, n0 = 30, при этом передаточная функция регулятора равна

W ,ег ( 5 ) =

19,75 5 + 92,5

5 + 30

19,75( 5 + 4,68)

5 + 30

а статическая ошибка определяется только особенностями системы и имеет фиксированное значение, управлять которым невозможно.

Ясно, что выбранный порядок полинома G ( 5 ) не позволяет учесть при синтезе регулятора требования, предъявляемые к статической ошибке. В этом случае можно усложнить регулятор либо за счет введения астатизма, либо путем повышения порядка M ( 5 ). Оба варианта предполагают повышение порядка полинома G ( 5 ).

Примем желаемый характеристический полином в виде

G ( 5 ) = ( 5 + 10)⁴ = 5 ⁴ + 40 5 ³ + 60 0 5 ² + 40 0 0 5 + 10 0 00.

Тогда условия (2), (3) принимают вид

W ( 5 ) = 16— M ( 5 ), 1 - W^ ( 5 ) = ^{5 - 16} N ( 5 ),

^Ж      ( 5 + 10) 4                ^Ж      ( 5 + 10) 4

а уравнение синтеза -

16 M ( 5 ) + ( 5 ² - 16) N ( 5 ) = 5 ⁴ + 40 5 ³ + 600 5 ² + 4000 5 + 10 000.               (14)

Добавим условие физической реализуемости передаточной функции регулятора, т. е. предположим, что deg( N ) >  deg( M ) . Тогда из (3) находим полиномы минимального порядка

M ( 5 ) = m 1 5 + m ₀, N ( 5 ) = 5 ² + n 1 5 + n ₀.

Подставив полученные выражения для M ( 5 ) и N ( 5 ) в формулу (14) и приравняв коэффициенты при одинаковых степенях 5 , получаем систему уравнений n 1 = 40, n ₀ - 16 = 600,

16 m 1 - 16 n 1 = 4000, 16 m ₀ - 16 n ₀ = 10 000.

Отсюда следует m 1 = 290, m0 = 1241, n = 40, n0 = 616 , при этом передаточная функция регу лятора равна

W        290 5 + 1241 = 290( 5 + 4,28)

^{рег( 5} ) = 5 ² + 40 5 + 616 ” 5 ² + 40 5 + 616

Рис. 2. Структурная схема замкнутой системы с регулятором в ППП Simulink

Рис. 3. Структурная схема синтезированной системы в ППП Simulink

Полученное решение однозначно. Следовательно, при минимальных порядках полиномов N ( 5 ), M ( s ) повышение порядка полинома G ( s ) не позволяет регулировать какие-либо характеристики замкнутой системы, кроме G ( s ). Однако для рассматриваемого варианта желаемого полинома замкнутой системы G ( s ) в рамках принятых ограничений порядок полинома M ( s ) числителя регулятора может быть повышен до M ( s ) = m ₂ s ² + m 1 s + m ₀. Тогда полиномиальное уравнение (13) принимает вид

16( m ₂ s ² + m 1 s + m ₀) + ( s ² - 16)( n ₂ s ² + n 1 s + n ₀) = s ⁴ + 40 s ³ + 600 s ² + 4000 s + 10 000. (15) В результате система уравнений для коэффициентов при s является недоопределенной. Она содержит шесть неизвестных и пять уравнений. Введем отношение k = m ₀/ п ₀ и запишем уравнение (15) в виде

16( m ₂ s ² + m 1 s + kn ₀) + ( s ² - 16)( n ₂ s ² + n s + n ₀) = s ⁴ + 40 s ³ + 600 s ² + 4000 s + 10 000 .

Как отмечено выше, величина к определяет статическую ошибку в замкнутой системе. Пусть заданный уровень статической ошибки определен как £ _№ = 0,1 у _ю . Тогда, учитывая только управление, из формулы (12) получаем

Отсюда следует к = - 9. Записывая и решая систему уравнений относительно коэффициентов при степенях s , получаем n 2 = 1, n 1 = 40, n ₀ = - 62,5 , m ₂ = 42,4, m 1 = 290, m ₀ = 562,5. Таким образом, передаточная функция регулятора имеет вид

W ,е _Г( s ) =

42,4 s ² + 290 s + 562,5 s ² + 40 s - 62,5 .

Структура модели замкнутой системы в пакете Simulink и график переходной функции представлены на рис. 2, 3.

Побочным эффектом обеспечения заданного уровня статической ошибки стало появление двух нулей замкнутой системы в точках - 3,41 ± 1,26 j , что привело к существенному перерегулированию в переходной функции (рис. 4). Добавив в прямую цепь регулятор

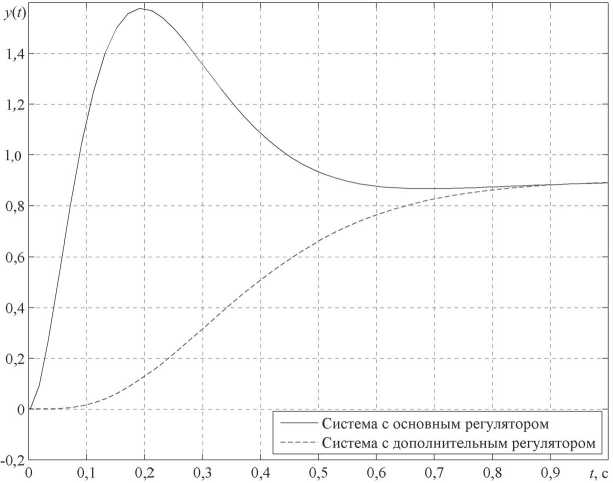
Рис. 4. Переходные характеристики в синтезированных системах

W ,ен ( 5 ) =

13,22

5 ² + 6,28 5 + 13,22’

можно добиться желаемого качества переходного процесса (рис. 4). Структурная схема полученной при этом системы представлена на рис. 3.

Из рис. 4 следует, что синтезированная система, содержащая два регулятора - основной и дополнительный, имеет статическую ошибку, равную 0,1, в то же время качество процесса соответствует желаемому.

Выводы. Результаты проведенного исследования свидетельствуют о том, что метод желаемой передаточной функции в модификации [3] позволяет синтезировать регулятор, обеспечивающий управление в системе с заданной точностью, т. е. обеспечивающий заданный уровень статической ошибки. При этом перерегулирование в системе может достигать больших значений. Во избежание этого в систему вводится дополнительное регулирующее звено компенсирующего типа. В результате система имеет заданное значение статической ошибки управления, а также приемлемое перерегулирование.