Синтез систем регулирования непрерывных станов с многовалковыми калибрами

При математическом описании объекта регулирования, каким является клеть прокатного стана, необходимо в первую очередь выделить те технологические факторы, которые являются определяющими в процессе деформации металла. К их числу можно отнести давление металла на валки Р, момент прокатки М, опережение металла в очаге деформации S, межклетевые натяжения F, коэффициент трения /, предел текучести металла о₅, скорость прокатки V , вытяжку в клети ц [1, 2]. Все эти параметры связаны между собой сложными нелинейными зависимостями.

В связи с тем, что в момент проектирования непрерывных станов полная информация об этих зависимостях отсутствует, при математическом описании целесообразно учесть наиболее весомые технологические параметры, а остальные считать постоянными. Учитывая сказанное и переходя к приращениям, очаг деформации z-й клети можно описать линейными уравнениями [2]:

Ы>,=1^ЬР,_х*кр,Ыу,

ДМ, =R_iAF,_₄-R_fZkF_i-            (1)

^=к83ЬР,_х+к8^Л где ДР]_Х, ДР] - приращения заднего и переднего натяжений z-й клети;

Rj - радиус валков;

к_р>1, к_р1, k_s>l, k_Sl - технологические коэффициенты (частные производные):

к_п 1 =----; к_п. = —- ; кс =--- —, k_s = —-.

^р’* A7v_r AF_Z ^F_l-X ДР]

Технологические коэффициенты можно определить с помощью аналитических формул [3].

При абсолютно жесткой полосе (упругое удлинение 8 = 0) приращение переднего межклетевого натяжения описывается уравнением [4]

А^ =-^-[—^(l+S^-A^a + S,)*

l + Tn>1Jp цм

AVB1+i,

*—^ks^,+x"№^-11,(2)

h+i где Ув - линейная скорость валков

^в= —-(3)

J о - угловая скорость двигателя;

R , j - радиус рабочих валков и передаточное число редуктора;

S - опережение металла в очаге деформации;

А/^, ДР_И ДГ^ - приращения натяжения между (z — 1) -й и z-й, z-й и (У + 1)-й, (/ + 1)-й и (z + 2) -й клетями;

k_nj , Т_П1 - коэффициент передачи и постоянная времени полосы в z-м промежутке (между z-й и (/+1) -й клетями),

^Sj ^,i ^S,i+1 ^,+1 Н/+1 гр _ ^Лп,1 '""EX где Е^ - модуль упругости Е^ = 2,02 40⁵ н/мм²;

Q_t - поперечное сечение полосы в межутке;

ПОЛОСЫ z-м про-

lj - длина z-ro межклетевого промежутка.

Учитывая, что КВ1 « ИВ1+1 / ц,+1; kSl « -ks^x , последнее уравнение можно привести к виду k = AJVe^=V^(б)

где Д , Д - коэффициенты, не зависящие от скорости:

4 =---->(7)

^S,z “^5,z+l ^Sj

Bt =                     .(8)

' £уй 2^£yQ

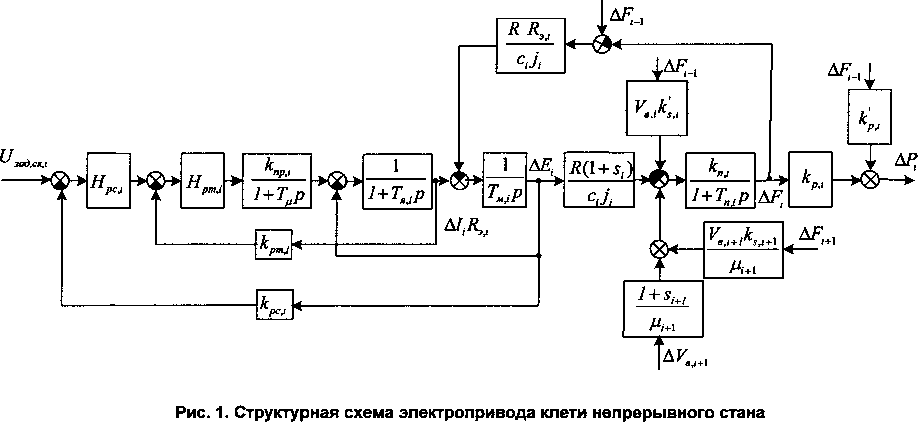
Считая, что система управления электроприводом клети - двухконтурная с контурами тока и скорости [4], и используя уравнения (1) и (2), структурную схему электропривода z-й клети с учетом силовой связи клетей через полосу представить в виде, приведенном на рис. 1.

На этой схеме приняты следующие обозначения:

I, Е - ток и ЭДС двигателя;

с - произведение магнитного потока на конструктивная постоянную, с-кФ\

Тм, Гя - электромеханическая и электромагнитная постоянные времени;

Г_ц , кур - постоянная времени и коэффициент передачи тиристорного преобразователя;

Д - эквивалентное сопротивление якорной цепи; к_т, к_с - коэффициенты обратной связи по току и скорости;

Ирт, Ярс - передаточные функции регуляторов тока и скорости.

Пренебрегая перекрестными связями в объекте регулирования ( ДКв/+1 = 0, AFZ-1 = 0 , Д/^ = 0 ) и внутренней связью по ЭДС двигателя [6], после структурных преобразований схема рис. 1 приводится к виду, позволяющему приступить к синтезу контуров регулирования (рис. 2).

Постоянная времени полосы Т_П1 [4] во время преобразований не учитывалась.

На структурной схеме рис. 2 приняты дующие обозначения:

к_Д- коэффициент передачи двигателя, к - ^j¹^ _ ^j® ^д ^(l + S^A ^(l+SM ’

Тм - электромеханическая постоянная с том силовой связи между клетями 7М = £ДГМ , kF - коэффициент передачи полосы _ Л0^^^_Л(1 + 5)Д

F V^cj toe ’ еле-

(9) уче-

Ярн - передаточная функция регулятора натяжения;

к_Р - технологический коэффициент, к_р=\Р!^Е.

На структурной схеме и в последних уравнениях индекс z опущен, так как все переменные, коэффициенты, передаточные функции относятся только к z-й клети.

Электромеханика

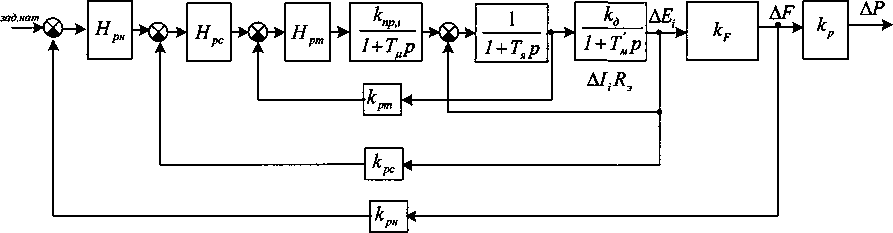
Рис. 2. Преобразованная структурная схема электропривода клети

Для получения модульного оптимума при регулировании тока в непрерывном режиме преобразователя передаточная функция регулятора тока должна иметь вид [3]

Ню = рс

2^А_+^ш1=,+^™1,  (и)

47_ц к_с рю ^р р со

где

\ + Т_яр 1

рт 2?;р ^

Для адаптивного регулятора тока, реализуемого схемой рис. 3, параметры резисторов R_x, R₂ и конденсатора С рассчитываются по условиям:

R^C = 27^&_Пр£_т, R₂C = 7^ .

Сопротивление резистора R₃, уменьшающего постоянную времени регулятора тока в прерывистом режиме, определяется по условию

7?3 = Т?2/(20-50) .

Получение модульного оптимума при регулировании скорости несколько осложняется тем, что в передаточную функцию регулятора скорости

^7?(1 + S) ни " CT^k/jks '

Из (14) видно, что получение модульного оптимума при любых скоростях двигателя возможно введением в канал интегрального регулятора блока деления. При отсутствии полосы в валках для получения оптимальных процессов необходимо интегральный канал исключить из регулятора скорости.

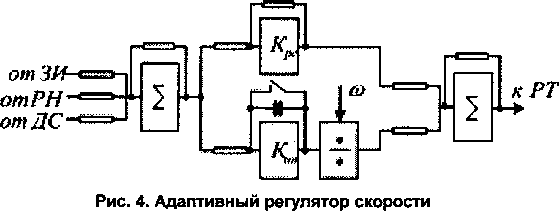
Принципиальная схема регулятора скорости приведена на рис. 4.

Модульный оптимум контура регулирования натяжения обеспечивается регулятором с передаточной функцией

г = 011мЖ ^ 47;^

Н9н =

k_cck_s со     ^_Рн

----— --= (0—, 47^_H(l + S)/>     р

входят коэффициент к_д и постоянная времени Т_м, зависящие от скорости двигателя со. Разделение пропорционально-интегрального регулятора скорости на пропорциональный и интегральный регуляторы дает:

где _ kccks рн 47^X1+$)'

Принципиальная схема регулятора натяжения приведена на рис. 5.

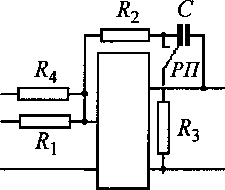
Рис. 3. Адаптивный регулятор тока

от ДН

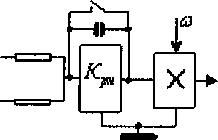
Рис. 5. Регулятор натяжения

Создание систем прямого регулирования размеров для станов с многовалковыми калибрами не было возможным, так как отсутствовали надежные датчики размеров, способные проводить измерения размеров раската по нескольким осям. В связи с этим для станов возможно лишь применение систем косвенного регулирования размеров.

Одним из энергосиловых параметров, кос венно характеризующих размеры раската, является давление металла на валки. При постоянном давлении стабилизируется размер раската при изменении таких технологических параметров, как коэффициент трения, предел текучести и диаметр исходной заготовки. Для обеспечения модульного оптимума передаточная функция регулятора давления в трехконтурной системе должна иметь вид

_ kccksm рд 47;^Адав(1 + 5)р р

где к_№ - коэффициент обратной связи по давлению металла на валки.

Регулятор давления реализуется схемой, подобной схеме рис. 5.