Синтез системы управления грузоподъемными механизмами

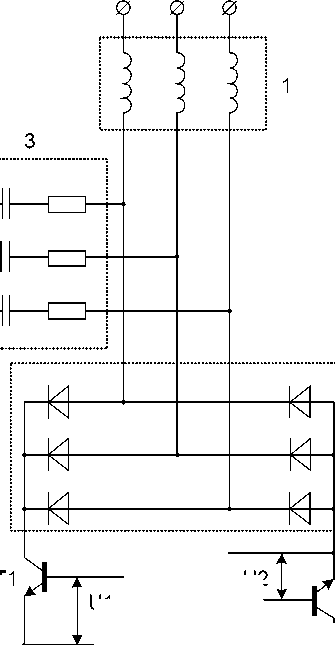
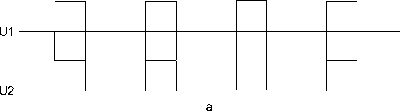
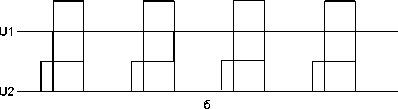
Холявко Артур Олегович, студент нулевому проводу через RC-цепи 3. Предлагаемая схема уменьшает бросок тока за счет плавного наращивания напряжения на статорных обмотках по требуемому закону. При синхронных и равных по длительности сигналах ШИМ осуществляется плавный пуск рис. 1а. При синхронных и не равных по длительности сигналах осуществляется динамическое торможение рис. 1б RC цепи служат для снижения коммутационных перенапряжений.

N

ABC

T2

T1

U2

U1

А

Б

Рис. 1. А – схема транзисторного регулятора напряжения; Б – осциллограммы сигналов на транзисторах

Рассмотрим задачу синтеза системы управления перемещением с ограничением раскачивания груза. Соответствующая схема механической системы представлена на рис. 2. На рисунке приняты следующие обозначения: М – масса тележки, m – масса груза, L – длина подвеса, F – сила, приложенная к тележке, φ – угол смещения груза от вертикали. Уравнения, описывающие такую систему, следующие [2]:

( M + m )V - mL y = F

,

J ГР(? + mgL^ = mLV где V – скорость тележки, Jгр – момент инерции груза, g – ускорение силы тяжести.

Момент инерции груза относительно точ- ки подвеса определяется выражением:

J _ГР = mL ²

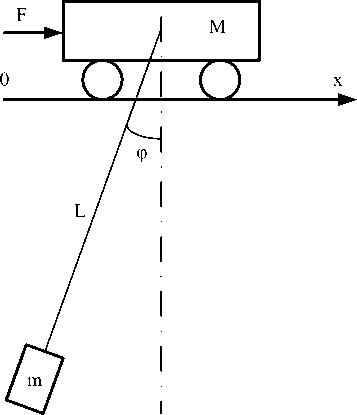
Рис. 2. Схема перемещения тележки с грузом

С учетом выражения (1) и сил сопротивления вязкого трения уравнения в операторной форме принимают вид:

MVp = F - m(Vp - L ^ p ²) - VK TP2

Ф ⁽ Lp ² + K Tp i p + g ) = Vp

где K ТР 1 , K ТР2 , – коэффициенты трения для m и M соответственно.

На основе уравнений (2), (3) и с учетом описания АД при амплитудном управлении [3] можно составить структурную схему разомкнутого электропривода перемещения тележки.

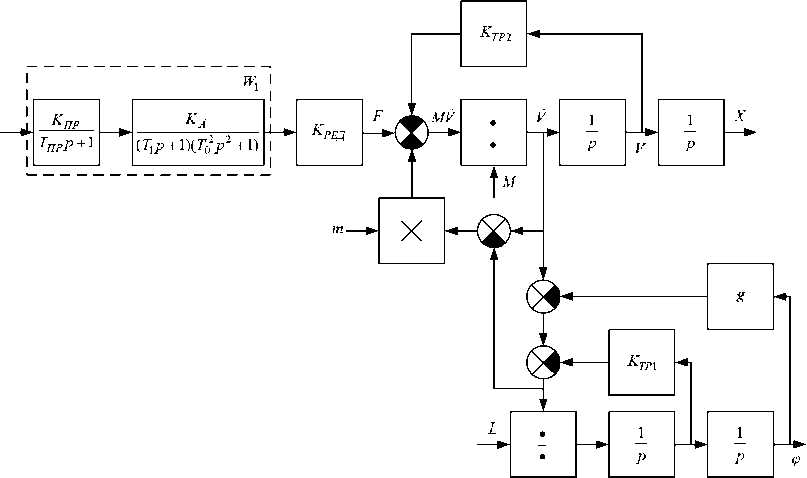
Рис. 3. Структурная схема разомкнутого электропривода перемещения тележки

где K пр , Т пр – параметры преобразователя, K Д , T 1 , T 0 – параметры двигателя, K ред – коэффициент редуктора.

В целях создания замкнутой системы управления используем датчик ускорения. Для адаптации системы необходимо контролировать вес груза ( m ) и длину подвеса ( L ). Рассматриваемые координаты связаны следующими передаточными функциями:

M ДВ

K РЕД

1                                  .

- ^V = W M (p) ^V

W X ( p )

Ф =

g + K ТР I p + Lp p

V " = W ф ( p )V ^

V = -K V   V- = W v ( p)!/■

Tvp +1

где K v , T v – коэффициент и постоянная времени апериодического звена.

В результате вычисления сигналов M дв , φ , V можно создать структуру подчиненного регулирования электропривода перемещения с адаптацией под конкретный режим работы (рис. 4). Ограничение момента в рассматриваемой структуре реализуется за счет контроля уровня выходного сигнала регулятора угла смещения. На основе структуры, приведенной на рис. 4, было выполнено моделирование исследуемого электропривода перемещения с вычисленными сигналами обратных связей, результаты которого приведены на рис. 5, 6. Видно, что введение обратной связи по φ позволяет практически исключить колебательность. Регулятор φ в этом случае выполняет роль управляемого задатчика интенсивности для координаты момента.

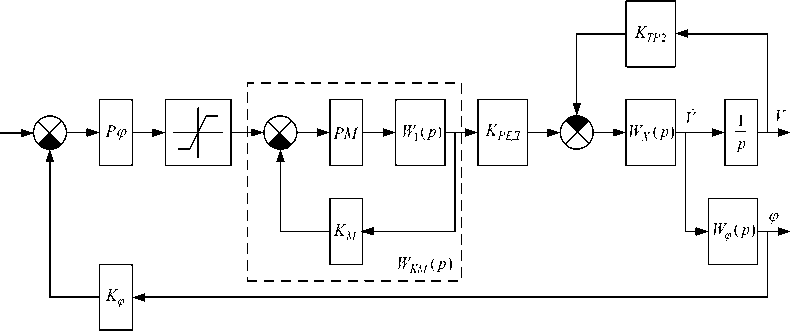
Рис. 4. Структурная схема подчиненного регулирования электропривода перемещения

Оптимальный процесс достигается, когда плавный пуск осуществляется с постоянным ускорением. В процессе эксплуатации изменяются значения m и L. По сигналам соответствующих датчиков происходит перестройка вычислителей координат Mдв и φ, и параметров регуляторов РМ и Рφ. Таким образом, можно осуществить управление тележкой в различных усло- виях работы с ограничением раскачивания и оптимальным по ускорению процессом движения. Анализ чувствительности передаточных функций системы управления показывает, что в предлагаемом электроприводе перемещения тележки наибольшие требования по точности предъявляются к датчику веса груза.

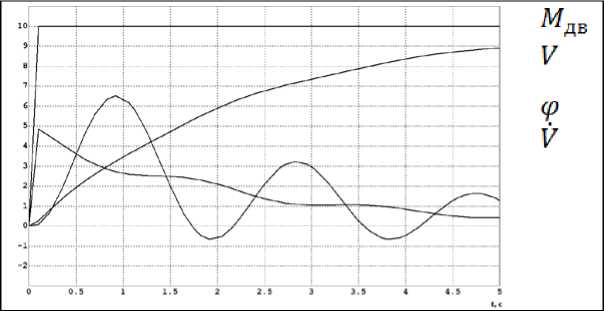
Рис. 5. Результаты моделирования электропривода без обратной связи

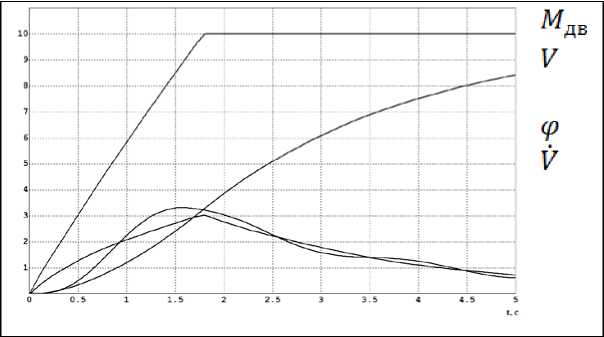
Рис. 6. Результаты моделирования электропривода с введенной обратной связью

Выводы: разработаны и исследованы модели элементов системы управления и механической части грузоподъемных устройств, в том числе силовые маловентильные преобразователи для системы автоматизированного управления электроприводами подъема и перемещения электротали. Это позволяет создать систему управления ГПМ с улучшенными качественными показателями за счет ограничения угла раскачивания и рывка. В результате этого сокращается время транспортировки и повышается сохранность грузов.