Синтез структуры и разработка математической модели автоматизированных многодвигательных гидромеханических систем

Введение. Современной тенденцией является создание технологических машин, представляющих собой комплексы взаимосвязанных и взаимодействующих механизмов, основу которых составляют многодвигательные гидромеханические системы (МГМС). Особенностью современных МГМС является наличие нескольких одновременно или с определенной последовательностью функционирующих гидродвигателей, работа которых определяется отдельным гидромеханическим исполнительным контуром (ГИК), в состав которого они входят.

Специфика МГМС для мобильных и стационарных технологических машин заключается в технологических и технических требованиях, предъявляемых к ним, с этим связаны различия в конструктивном исполнении ГИК. Однако все МГМС технологических машин в основе своей функционально идентичны и включают три основные подсистемы: энергосиловую установку, ГИК и подсистему управления.

Энергосиловая установка (ЭСУ) обеспечивает преобразование и подачу энергии для каждого из двигателей МГМС в зависимости от алгоритма функционирования. При этом именно ЭСУ, в первую очередь, обеспечивает энергетическую эффективность, а также технологическое качество функционирования машины. В зависимости от задач, решаемых ЭСУ, в ее структуру может входить один общий для всех контуров насос, несколько насосов, каждый из которых обеспечивает отдельный контур, либо компромиссный вариант из приведенных решений, когда отдельные насосы в зависимости от режима могут работать на отдельный или на несколько контуров. Наибольший интерес представляют ЭСУ с переменной структурой, изменение которой обеспечивается подсистемой управления.

ГИК отличаются многообразием конструктивного исполнения, что обусловлено многообразием функций и технических требований, предъявляемых к ним. Наиболее типичными вариантами ГИК для современных технологических машин являются:

– контур гидростатических или гидромеханических силовых передач;

– контур автоматических следящих гидросистем;

– два или более совместно или раздельно функционирующих гидродвигателя, работающих со знакопеременной или постоянной по знаку нагрузкой в независимом или синхронносинфазном реверсном режиме и представляющих собой единый контур.

В технологических машинах возможны различные комбинации перечисленных типичных контуров. Все варианты контуров присутствуют в мобильных гидрофицированных машинах, транспортных энергетических средствах, зерноуборочных комбайнах, сеялках и культиваторах, погрузочных и коммунальных машинах [1].

Подсистемы управления МГМС в зависимости от типа технологической машины отличаются по степени сложности и способу управления.

В простейших подсистемах управления с дискретными распределителями используются специальные устройства, обеспечивающие внутриконтурные управляющие гидромеханические связи, а между отдельными контурами или отдельными функциональными блоками управление обеспечивается электромеханическими или электромагнитными устройствами. В сложных технологических машинах используются микропроцессорные системы управления на базе пропорциональных и дискретных гидроаппаратов, позволяющие, прежде всего, обеспечить оптимальное управление структурой и параметрами ЭСУ и ГИК.

Постановка задачи. В типичных структурах гидромеханических систем используется так называемое параметрическое управление, позволяющее в зависимости от способа получать достаточную степень точности установившегося режима и необходимое качество переходных процессов. Однако данный вариант ограничен жесткой структурой, характеристиками управляющих устройств и мощностями, получаемыми от энергосиловой установки, и поэтому не позволяет обеспечить необходимый уровень экономичности. Как показали исследования [2], использование гидромеханических однодвигательных систем с изменяемой структурой, когда из нескольких упрощенных структур определенное количество вновь «сшиты» благодаря системе управления, позволяет существенно расширить эффективность МГМС.

Цель исследования – синтез структуры и оптимизация параметров МГМС. Для выбора оптимальной структуры необходимо выделить область, состав и алгоритмы функционирования наиболее типичных МГМС, а также определить наиболее подходящие критерии оптимизации. В качестве критериев оптимизации структуры МГМС целесообразно выбрать экономичность, быстродействие и инвариантность к условиям и алгоритмам функционирования.

Особый интерес представляют МГМС распространенных технологических машин: сельскохозяйственных, дорожно-строительных, погрузочных, коммунальных, станков, сварочного, литейного, кузнечно-прессового оборудования, роботов и манипуляторов.

Алгоритмы функционирования МГМС отличаются значительным разнообразием, но наиболее часто встречающиеся варианты следующие: последовательное функционирование силового, следящего и синхронно-синфазного контура, совместное параллельное функционирование в различных сочетаниях. Для стационарных технологических машин к типичным алгоритмам следует отнести последовательное или параллельное в различных сочетаниях функционирование трех гидромеханических исполнительных контуров, обеспечивающих пространственное позиционирование или слежение.

Для реализации синхронно-синфазного реверсного режима движения исполнительных двигателей, имеющих переменную по величине и знаку нагрузку, целесообразно использовать в структуре ГИК дроссельный делитель-сумматор потока и систему замедления. Дроссельный делитель-сумматор потока обеспечивает параллельное подключение двигателей, при котором создается максимально возможное давление, величина его строго регламентирована параметрами насосной установки. Наиболее эффективным в двухдвигательных контурах является делитель потока непрямого регулирования, представляющий собой трехкомпонентный астатический регулятор [3]. Система замедления необходима для экономичного торможения гидродвигателей при переходе их в насосный режим функционирования при реверсной знакопеременной нагрузке. На рис.1 представлена обобщенная структурная схема МГМС с наиболее сложным ГИК, являющимся контуром реверсного синхронно-синфазного движения. В качестве средств, обеспечивающих работу синхронных механизмов мобильных машин, используются различные по принципу действия системы и устройства.

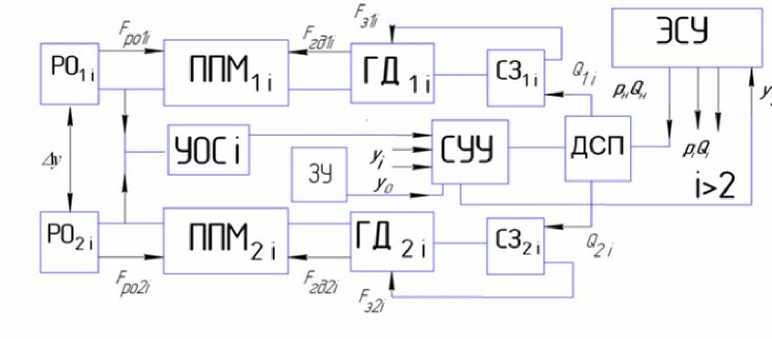
Рис.1. Обобщенная структурная схема МГМС

Как показали исследования, использование в синхронно-синфазных контурах делителя потока непрямого регулирования, представляющего собой астатический регулятор, позволяет обеспечить максимальную точность синхронизации в установившемся и неустановившемся режимах работы при минимальных потерях энергии на управление, т.е. при максимальном КПД [1, 3]. Контуры силовой и следящей передачи, имеющие сравнительно простую структуру, представлены условно как параллельно подключенные потребители, характеризующиеся параметрами Р, Q i .

Гидравлическая подсистема, включающая источник питания ЭСУ, делитель-сумматор потока непрямого регулирования ДСП, системы замедления СЗ i и гидродвигатели ГД i , формирует параметры потока жидкости P i , Q i и преобразует его энергию в движение выходного звена ГД i . При изменении параметров потока используются различные способы управления благодаря обратным связям. Управляющая подсистема реализует алгоритм управления МГМС. Многообразие структурных состояний МГМС определяется приоритетом технических параметров, применяемыми способами управления и техническими средствами их реализации и может быть разделено на три основные группы. Первая группа охватывает приемы управления обобщенными силовыми и скоростными параметрами РО , вторая – силами сопротивления движению F з i , третья – комбинированное сочетание первых двух. Последняя является наиболее эффективной, так как использует преимущества первых двух.

По обобщенной структурной схеме была составлена принципиальная гидрокинематиче-ская расчетная схема (рис.2).

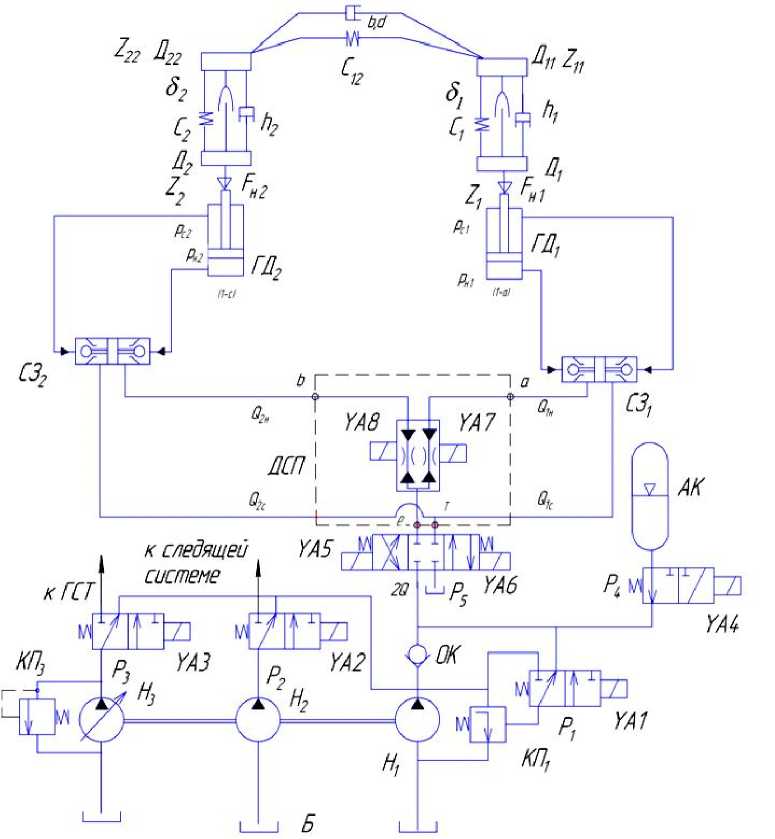
Рис.2. Принципиальная гидрокинематическая расчетная схема МГМС

Механическая подсистема в данном контуре представляет собой упругую динамическую систему, имеющую два гидродвигателя ГД 1 , ГД 2 , каждый из которых приводит в движение двухмассовую систему, приведенную к гидродвигателю D 1 , D 2 и к рабочему органу механизма и D 11 , D 22 . В процессе функционирования гидродвигатели преодолевают внешнюю технологическую нагрузку F н i . Двухмассовый механизм ГИК для каждого гидродвигателя отдельно и для единой связанной конструкции характеризуется демпфированием, жесткостью и зазором соответствующего участка h ij , c ij , δ I внутри механизма и между механизмами, фазовыми координатами выходных звеньев гидродвигателей и рабочих органов механизмов Z i , Z ij .

Гидравлическая подсистема включает энергосиловую установку Н 1 –Н 3 , ГА, КП 1 –КП 3 , обеспечивающую подачу жидкости к гидродвигателям ГСТ, следящую систему и синхронно-синфазный контур ГД 1 , ГД 2 , системы замедления, СЗ 1 , СЗ 2 и делитель-сумматор потока непрямого регулирования с дискретным электромагнитным управлением ДСП. Компоновка делителя-сумматора потока, приведенная на схеме, является частным случаем компоновки, зависящим от типа механизма. Выбор конкретной схемы компоновки делителя потока непрямого регулирования, обеспечивающего функционирование определенного типа синхронных механизмов машин, определяется особенностями работы этих механизмов синхронно-синфазного позиционирования, обеспечивающих согласованную работу для одного из направлений движжения, синхронизацию прямого и обратного движений; механизмов согласования скоростей движения активных рабочих органов одностороннего вращательного движения [1].

Управляющая подсистема на базе программируемого контроллера, позволяющая изменять структуру МГМС, алгоритм и параметры функционирования, включает в себя электрогидравличе-ские устройства, управляемые электромагнитами YA 1 – YA 8 , а также ряд гидравлических устройств СЗ 1 ,СЗ 2 , ДСП с обратными связями по нагрузке, скорости и положению, которые обеспечивают автоматическое дроссельное регулирование и релейное управление внутри синхронносинфазного ГИК, работающего в реверсном режиме со знакопеременной нагрузкой.

Рассматриваемые МГМС являются динамическими системами с интегрированными, переменными гидромеханическими, силовыми и энергетическими связями. Используя наиболее распространенные принципы для обобщенной математической модели МГМС, представляющей собой систему дифференциальных нелинейных уравнений, описывающих функционирование МГМС для наиболее сложного ГИК синхронно-синфазного движения в реверсном режиме со знакопеременной нагрузкой, принимаем следующие допущения:

• –    податливость гидравлической подсистемы ниже податливости механической подсистемы;

• –    функционирование МГМС рассматривается в окрестности точки нагрузочной характеристики ЭСУ 2 Q = const; p = const (подтверждается для исследуемой области предварительными испытаниями ЭСУ);

• –    рабочая жидкость сжимаемая, капельная, в каналах присутствует нерастворенный воздух. Состояние среды описывается зависимостями, справедливыми для смесей с осредненными свойствами;

• –    утечки в подвижных соединениях малы, они зависят, главным образом, от конструктивного исполнения и могут быть определены [2] коэффициентом утечки К у ;

• –    скоростные потери давления (напора) в управляющих гидролиниях, соединяющих усилительный и регулирующий элементы делителя потока непрямого регулирования, незначительны, и ими можно пренебречь. Достаточность такого допущения подтверждается предварительными экспериментальными исследованиями. Потери давления в гидролиниях составляют до 0,05 МПа.

С целью упрощения анализа основных видов ГИК рассмотрим работу наиболее сложного, характеризующегося наличием двух дополнительных гидролиний, отводящих дренажные потери от гидродвигателей, и установкой дросселей чувствительного элемента в сливных гидролиниях.

Уравнение баланса энергии параллельных ветвей ГИК при установившемся режиме работы с учетом уравнения баланса делителя потока [3] имеет вид:

Δ p = Δ p ч + Δ p рэ + Δ p м ;                                  (1)

Δ p = Δ p _вн 1 – Δ p _вн 2 ,                                        (2)

где Δp – разность внешних перепадов давлений по нагрузке; Δpч – разность перепадов давлений в ветвях на чувствительном элементе; Δpрэ – разность перепадов давлений в ветвях на ре- гулирующем элементе; Δpм – разность перепадов давлений в ветвях на сопротивлениях гидромагистралей системы.

Δ p ч = 4 Q ² K ч ϕ ,                                    (3)

где K ч – коэффициент сопротивления дросселей чувствительного элемента; Q – расход в ветви чувствительного элемента; ϕ – ошибка синхронизации.

Разность перепадов давлений в ветвях на регулирующем элементе Δ p рэ определим, описывая потери давления на каждой из щелей:

АРрэ = Y Qi2/2дц2р bp2(ho — У)2+Зр2) - Y Q22/2дц2р bp2(ho+y)2+3p2,(4)

где Q 1 – расход в левой (менее нагруженной) ветви через регулятор; Q 2 – расход в правой (более нагруженной) ветви через регулятор:

Q1 = Q + ΔQ + q1,(5)

Q2 = Q – ΔQ + q2,(6)

ц р - коэффициент расхода щели регулирующего элемента; Ь _р - периметр окна регулирующего элемента; γ – удельный вес жидкости; h 0 – смещение рабочих кромок подвижного звена регулирующего элемента при отсутствии разности перепада по давлению между ветвями; у – смещение подвижного звена регулирующего элемента, положительное смещение соответствует увеличению сопротивления в менее загруженной ветви; δ р – зазор в золотниковой паре.

Введем понятие коэффициента сопротивления регулирующего элемента:

Крэ = y/2дц2р Ьр2),(7)

и окончательно уравнение (4) примет вид:

А р рэ = К рэ (2 q i Q +2 ф q i Q + q 1 ²+(1+ ф )²Q²/(( h o -y)²+ 5 р ²))-

–2q2Q–2ϕq2Q+q12+(1–ϕ)2Q2/((h0+y)2+δр2))).(8)

Разность перепадов давлений в ветвях на сопротивлениях гидромагистралей системы, определяемых по второй водопроводной формуле (11), (16), описывается выражением

.Арм = Км( Q 12 - Q 22),(9)

где К м - коэффициент сопротивления гидромагистралей системы, К м = 8 Y^ _тр l _экв/ д п ² о Т _р⁵); Х _тр - коэффициент потерь на трение в трубах; l экв – эквивалентная длина труб гидромагистралей с учетом местных сопротивлений; d тр – диаметр проходного сечения гидромагистралей.

После преобразований с учетом (5), (6) выражение (8) будет иметь вид:

Δ p м = К м (4 ϕ Q ²+( q 1 ²+ q 2 ²)+2 ϕ Q ( q 1 + q 2 )+2 Q ( q 1 - q 2 )).                  (10)

Таким образом, уравнение баланса энергий ветвей примет вид:

А р= К рэ (2 q i Q +2 ф q i Q + q 1 ²+(1+ ф )² Q/((h o - у)²+ 3 р ²)) - 2 q 2 Q - 2 ф q 2 Q + q i ²+(i - ф )² Q ²/(( h o +y)²+ 5 р ²)))+ + 4 Q К ч ф К м (4 ф Q 2 +( q i ²+ q 2 ²)+2 ф Q ( q i + q 2 )+2 Q ( q i - q )).                 (11)

Уравнение энергетического баланса ветвей системы (11) с учетом того, что состояние покоя делителя потока обусловлено параметрами у' = 0, у” = 0, ф = 0 (астатизм регулятора), представляем в виде:

А р = К рэ (2 q i Q + q i ² + Q 2 /(( h o - у)²+ 5 р ²)) - ( q 2 + Q )²/(( h o + у)²+ 3 р ²))) +К м ( q i ²- q 2 ² + 2 Q ( q i - q 2 )). (I2)

Из уравнения (12) получаем статические нагрузочные и скоростные характеристики, определяющие конечное позиционирование подвижного звена регулирующего элемента при различных воздействиях по расходу и нагрузке.

Уравнение баланса энергии ветвей синхронизируемой системы для механизмов синхронно-синфазного позиционирования, обеспечивающих согласованную работу для одного из направлений движения, будет иметь вид:

А р = К рэ ((i+ ф )² Q ²/(( h o - y)² + 5 р ²)) - (i - ф )² Q ²/(( h o +y)²+ 5 р ²)))+4(К м +K ч ) Q ² ф .           (i3)

Для прямого и обратного движений:

Δ р = K рэ K²((1+ ϕ )² Q ²/(( h 0 - y)²+ δ р ²)) – (1 – ϕ )² Q ²/(( h 0 +y)²+ δ р ²))) + 4(К м K²+K ч ) Q ² ϕ .         (14)

Наиболее характерно для работы синхронных механизмов мобильных машин динамическое нагружение, соответствующее неустановившемуся режиму системы синхронно-синфазного функционирования, которое необходимо проанализировать. При этом в гидроприводе механизмов возникают гидромеханические нестационарные процессы. В гидроприводе с дроссельным делителем потока непрямого регулирования, функционирующим как астатическая система синхрониза- ции [3], от характера протекающих процессов будут зависеть оценочные параметры работы ме- ханизма.

Неустановившийся режим работы такой системы может быть описан уравнением движения переходных режимов ГИК [3]. Уравнения (15), (16) получаем на основании принципа Даламбера по имеющимся аналитическим зависимостям установившегося режима работы элементов

ГИК, уравнение (17) – уравнения (11) при условии совместного синхронно-синфазного функционирования гидродвигателей, при котором p 1 = p 2 .

F р – F ду – F пр – F тр у – F иу = 0; F у – F др – F тр р – F ир = 0,

где Fиу – сила инерции усилительного элемента; Fр – сила давления чувствительного элемента; Fду – гидродинамическая сила усилительного элемента; Fпр – сила противодействия центри- рующих пружин; Fтр.у – сила трения усилительного элемента; Fи.р – сила инерции подвижного звена регулирующего элемента; Fу – сила управления, действующая на регулирующем элементе; Fтр.р – сила трения регулирующего элемента; Fдр – осевая составляющая гидроди- намических сил регулирующего элемента;

Δ p ч + Δ p р.э + Δ p м + Δ p и = Δ p ,                              (17)

FF где Δр =   H2 - H1 – разность внешних перепадов давления по нагрузке; Δрч= Kч(Q1н2- Q2н2) –

Kгд2 Kгд1

разность перепадов давления в ветвях на чувствительном элементе, K ч = γ /(2 g µ ² ч ω ²), ω = π d ²/4, K p = K ч π d у ²/4; Δ р р.э – разность перепадов давления в ветвях на регулирующем элементе; Δ р м - разность перепадов давления в ветвях на сопротивлениях гидромагистралей системы; Δ p м – разность перепадов давления в магистралях:

Δ p м = К м (4 ϕ Q ²+( q 1 ²+ q 2 ²)+2 ϕ Q ( q 1 + q 2 )+2 Q ( q 1 - q 2 )).

Cила инерции в золотниковой паре усилительного элемента:

= d ² x

Fиу m1     , dt2

где m1 – масса подвижного звена усилительного элемента; x – смещение подвижного звена уси- лительного элемента.

Сила вязкого трения усилительного элемента, определяется из выражения Fтр. у = V1 dx , dt где V1 – коэффициент демпфирующей силы усилительного элемента,

V 1 = ^i—1 J i γν /( g δ i ) + 16 γπν l д d у ⁴/( gd д ⁴).

Здесь f i – площадь соответствующего элемента трения; δ i – радиальный зазор между элементами трения; ν – коэффициент кинематической вязкости жидкости; d у – диаметр усилительного элемента; l д – длина линейного дросселя демпфирования; d д – диаметр канала линейного дросселя демпфирования.

Силу вязкого трения, возникающую в золотниковой паре регулирующего элемента, определяем из выражения:

F тр ⁼ V 2 dy , где V 2 = ⁿ f γν /( g δ i ). dt                 ⁱ

Сила инерции регулирующего элемента:

d 2 y

Fир = m2     , dt2

где m 2 – масса подвижного звена регулирующего элемента; y – смещение подвижного звена регулирующего элемента;

Δpи = М1 dQ1 – М2 dQ2 , dt dt где Ари - разность перепадов давления в ветвях за счет инерционных масс системы; M1, M2 -инерционные массы подвижных частей соответствующих механизмов, приведенные к выходным элементам гидродвигателей:

– для вращательного движения

M i =( J qi + J ж i + J н i )/K гд i ²;

– для возвратно-поступательного движения

M i = m с i /K гд i ² .

Здесь J qi – момент инерции подвижных частей соответствующих гидродвигателей; J ж i – момент инерции жидкости, приведенный к выходному валу; J н i – момент инерции нагрузки, приведенный к выходному валу;

Jжi = 8y Кгд,2 l Vгм/(Vтрdгр2), где l - длина гидромагистралей; VrM - объем камер гидромотора; V-р - объем жидкости в гидромагистралях камерного тракта.

В окончательном варианте функционирование ГИК с дроссельным делителем потока непрямого регулирования при динамическом нагружении описывается системой уравнений:

mi d^X = KpQ2Ф-Kgух - Cx- Vi dX ;(18)

dt2

, ² у — f    ( dyl Y- к ( dy Y-^ dy-

'² dt ^{2 ак} F y I dtx J K^K I dt J V dt'

Ap - Крэ(2qiQ+2VqiQ+ qM1+^Q/((ho -У)2+Зр2)) - 2q2Q - 2фq,Q+ qi2+(1 - T)2QV((ho+y)2+ 5р2)))+ + 4Q2 Кч ф Кн(4^Q 2+(qi2+ q22)+2^Q(qi+q2)+2Q(qi - q2) + Q'M1-2 + (Q’p + ^’Q)Mi+2.(20)

Выводы. Cинтезированные структурная и принципиальная схемы и математическая модель дают возможность разработки нежестких субоптимальных структур МГМС.