Синтез управления малым космическим аппаратом с использованием двигателя-маховика на основе метода управления с поводырем

Рассмотрим систему стабилизации по углу тангажа малого космического аппарата (МКА) c двигателем-маховиком. В полете на МКА действует возмущающий момент, статистические характеристики которого неизвестны, но известны пределы, в которых изменяется величина возмущающего момента.

Данную задачу будем рассматривать как дифференциальную игру двух игроков, так как в качестве одного игрока, стратегия которого неизвестна, выступает возмущающий момент, а в качестве другого игрока – космический аппарат, управление которого нужно выбрать.

Рассмотрим систему управления МКА с помощью двигателя-маховика вокруг поперечной

* © Толпегин О. А., Литвинова П. Ю., 2017

оси, динамика которой определяется системой уравнений:

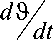
= СО

0’ где Jз = Jz - I; u=M^z=diydt = Id^z/. j3 — момент инерции космического аппарата без учета момента инерции маховика; Jz - момент инерции космического аппарата по оси Oz; I – момент инерции маховика; u – управляющий сигнал; MупрZ – управляющий момент двигателя-маховика по оси Oz, который появляется при разгоне махо вика и приложен к корпусу летательного аппарата; K – кинетический момент двигателя-маховика;

Qz - проекция абсолютной угловой скорости маховика по оси Oz; w_z - угловая скорость космического аппарата по оси Oz; Б - угол тангажа; и 0 - круговая скорость вращения космического аппарата; к _ю и ku - передаточные числа системы управления; ξ – возмущающий момент [1].

Управляющий момент удовлетворяет заданному ограничению:

|u| ≤ α.                       (2)

Возмущающий момент ξ характеризует внешние силы и внешние неконтролируемые возмущения, действующие на космический аппарат и удовлетворяющие ограничению:

|ξ| ≤ β = ρ·α, 0 < ρ < 1.            (3)

Задание ограничения на возмущения в виде (3) дает возможность оценить влияние возмущений на управление МКА по углу тангажа.

Заданы граничные условия:

[при? = /_о=О, _юДО) = (й_зо=-и_оЛ(О) = $о; (4) [при t = T, to„(0) = to_3T = -u₀,S(T) = Б₃.

Требуется найти управление, обеспечивающее минимум критерия быстродействия системы: т

3 = j 1^ —> minu.             (5)

о

Момент окончания переходного процесса T не фиксирован.

Управление системой (1) при наличии возмущений будем рассматривать как антагонистическую дифференциальную игру двух игроков: первый игрок выбирает управление u ( t ), а второй игрок – возмущение ξ( t ).

Первый игрок стремится минимизировать (5), а второй – максимизировать этот критерий.

Для решения задачи используем игровой метод управления с поводырем [2, 3].

Множество управлений U МКА, заданного ограничением (2), разобьем на два подмножества: U 1 и U 2. Подмножество U 1 используем для решения сформулированной задачи при отсутствии возмущения. Эту траекторию назовем траекторией поводыря. Подмножество U 2 используем для компенсации действия возмущений. Подмножество U 2 будем задавать с помощью коэффициента р , который изменяется в диапазоне от 0 до 1. Если ρ = 1, то все ресурсы управления используются для компенсации возмущений и U 1 = 0. При ρ = 0 возмущения отсутствуют и U 2 = 0.

Для исследования действия возмущений предлагается следующий алгоритм.

• 1.    Зададим коэффициент р, который изменяется в диапазоне от 0 до 1, и для множества U 1 ограничение на управление МКА зададим в виде

• 2.    При этом ограничении решим задачу оптимального быстродействия при отсутствии возмущений и построим оптимальную траекторию. Эту траекторию назовем траекторией поводыря и запишем в память БЦВМ.

• 3.    Решаем задачу о максимальном сближении траектории движения МКА с траекторией движения поводыря при действии возмущений с ограничением (3) при заданном значении коэффициента ρ. При этом используем все возможности управления МКА, то есть решаем задачу с огра-     83

<а(1-р).

ничением (2).

По времени переходного процесса можно оценить влияние возмущений на возможности управления МКА.

Рассмотрим расчет траектории поводыря при заданном значении коэффициента ρ.

Из выражений (2) и (3) возмущение ξ и управление u связаны следующим соотношением:

ξ = ρ ∙ u.                    (7)

Из соотношения (7) следует, что и (1 - р) используется для расчета траектории поводыря, а ( и • р) расходуется на гашение возмущений.

Перепишем систему управления (1) с учетом формулы (7):

7а₁⁼^"^ке'^Ю,"^к"'^иУ'"^Р')У'^,1 ^; (8) ^d%r™-^+u«'

От задачи Лагранжа перейдем к задаче Майера. Введем новую переменную x ₀ ( t ), определяемую дифференциальным уравнением

^хо/ - I и удовлетворяющую начальным условиям:

х о( t о) = t 0= 0.                  (9)

Тогда подлежащий минимизации критерий (5) можно переписать в виде

• 3, =x₀(T)^min„

и система (8) будет иметь вид dx^ / _ /dt=

" ^аю7^А<^ю=-^к«'^и'У-^рУУ'^гУ'- (11)

d%z = o>;+u„.

Эта система должна удовлетворять граничным условиям (4) и (9).

ГКО

ГРАДА

Т ом 1

Для решения задачи используем принцип максимума Л.С. Понтрягина [4, 5]. Cоставим функцию Гамильтона:

H = wTf,

и проинтегрируем от ϑ₀ до ϑ _Т правую часть и от ω _{z 0}

до ω _zt левую часть:

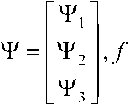
1(Ло'^"^'^-?))--^1

.          toz+D0

я = ^2И/®^'Н1-р)И' +

где переменные Tj (t),^ (?),Т3 (?) удовлетворяют системе уравнений:

JT/ ₌ _дН/

/ dt     /ох

х^т =[x₀,(o_z,9];

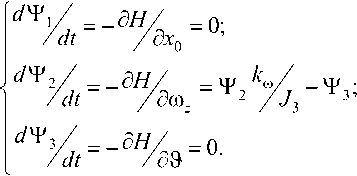
Решение системы (13) имеет вид:

Т^?) = Со = const;

■ Т,(/) = С1-е'Л+СУ 73;

^(О = С2 = const.

Функция Гамильтона достигает максимум

при управлении вида

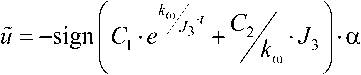
Оптимальное управление U ( t ) является кусочно-постоянной функцией и меняет знак не более одного раза, так как функция ¥ ₂( t ) имеет не более одного нуля.

Для решения задачи синтеза используем метод фазовых траекторий, при этом решение сво

дится к определению линии переключения, разделяющей фазовое пространство координат ω _z и ϑ на две области; в одной области оптимальное управление й (^) = +01, а в другой й ^ = —01. При попадании фазовой траектории на линию переклю-

чения знак оптимального управления изменяется на противоположный.

Для построения линии переключения второе уравнение системы (11) поделим на третье уравнение этой системы:

Яо2/ yA^-V^G-p))/

/^               /(^(^z+Uo))

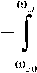
•Ш + Ур) V^z+V^O-p)

3₇ dw. = j dd;

9f = 9«-'%'(m„-m:0) +

/к2

и^'И-рН/О)-,)/           )

I                 /(^•M-(1-p) + ^«>-®zo)J’

где 9 0 и о _z 0 точка, в которую должна прийти система на фазовой плоскости; 9f - абсцисса на фазовой плоскости, находящаяся на линии переключения; ω _zt – текущее значение угловой скорости.

Алгоритм выбора оптимального управления имеет следующий вид:

= ос, если < если

и

и

и

и

и

Построение линии переключения определяет траекторию поводыря.

При управлении с поводырем управление МКА нужно выбирать с использованием алгоритма (16), так как в этом случае траектория МКА будет наискорейшим образом подходить к линии переключения, тогда после попадания на линию переключения, построенную для поводыря, траектория МКА будет колебаться относительно этой линии и отклонение МКА в момент Т от заданного значения будет не больше допустимой величины о, определенной дискретностью выбора управлению.

Рассмотрим результаты моделирования с использованием данного алгоритма.

Исследование проводилось при следующих значениях параметров гипотетического МКА: m _ка = 31,6 кг – масса космического аппарата; I _м = 0,195*10^-2, I_z = 0,8953 кг^м² - моменты инерции маховика и летательного аппарата с учетом момента инерции маховика по оси Oz;

υ 0 = 0,001 рад/с, k ω = 0,083, ku = 1.

Моделирование проводилось при различных ρ и ограничениях:

| u | < а, а = Я упр_тах = 20-10^-3 Н-м, |^| < в = ku 'Р'а.

Начальные условия имели следующие значения:

t ₀= 0, ω _z (0) = – 0,75 рад/c, ϑ(0) = 0,26 рад.

Фазовые координаты точки, в которую должна прийти система:

ϑ₀ = 0,22 рад., ω _{z 0} = – υ₀= –0,001 рад/c.

Моделирование процесса происходило до достижения заданной угловой скорости и угла тангажа с допустимым отклонением е = ^(о)_зт -ю, (Т)У +(^з ^_$(^))” ^Ю~³ рад/с.

График линий переключения для ρ = 0; 0,2; 0,4; 0,6; 0,8 представлен на рис. 1.

На рис. 2, 3 представлены графики изменения ω _z ( t ) и ϑ( t ), построенные при различных ρ = 0,3; 0,5; 0,7. Возмущения задавались в виде случайных функций, распределенных по нормаль-

Список литературы ному закону с нулевым математическим ожиданием, ограниченных величиной |ξ| ≤ ρ·ku·α, при этом величина α была равна максимально возможному значению α = 20·10–3 Н·м. Таким образом, величина ξ была ограничена |ξ| ≤ 0,006 Н·м.

Во всех рассмотренных случаях двигатель-маховик не переходит в режим насыщения.

Результаты моделирования показывают, что по времени переходного процесса при управлении с поводырем можно оценить влияние возмущений на возможности управления МКА с двигателем-маховиком.

• 1.    Алексеев К. Б., Бебенин Г. Г. Управление космическим летательным аппаратом. М. : Машиностроение, 1964. 404 с.

• 2.    Красовский Н. Н., Субботин А. И. Позиционные дифференциальные игры. М. : Наука, 1974. 456 с.

• 3.    Субботин А. И., Ченцов А. Г. Оптимизация гарантии в задачах управления. М. : Наука, 1981. 288 с.

• 4.    Математическая теория оптимальных процессов / Л. С. Понтрягин, В. Г. Болтянский, Р. В. Гамкрелидзе, Е. Ф. Мищенко. М. : Наука, 1969. 384 с.

• 5.    Толпегин О. А. Прикладные методы оптимального управления. Тексты лекций. СПб. : БГТУ «ВОЕНМЕХ», 2004. 215 с.

История статьи