Синтез управления маневром уклонения беспилотного летательного аппарата с учетом терминальных ограничений

2,3Don State Technical University, Rostov-on-Don, Russian Federation

Введение. Рассматривается задача формирования субоптимальной стратегии уклонения беспилотного летательного аппарата (ЛА) в условиях неопределенности текущих характеристик движения и будущей стратегии поведения противодействующего ЛА. При этом траектория уклоняющегося ЛА должна удовлетворять требованиям оптимальности некоторых заданных функций фазовых переменных в конечный момент времени, определяющих условия прохождения его траектории через заданную терминальную область пространства.

Начальные условия и динамические возможности уклоняющегося и противодействующего ЛА в начальный момент времени считаются известными. Управление уклоняющимся ЛА формируется за счет автономных средств его бортовой системы управления в реальном масштабе времени.

Целью работы является построение эффективного в вычислительном отношении метода решения задачи синтеза терминально-оптимального управления движением беспилотного уклоняющегося ЛА в вышеназванных условиях.

Рассмотрение задачи в такой постановке отличает ее от классических конфликтных задач о преследовании, решаемых с привлечением теории дифференциальных игр, и требует поиска эффективных в вычислительном отношении способов ее решения [1]. Необходимость такой постановки задачи обусловлена ограниченными возможностями бортовых цифровых вычислительных машин (ЦВМ) беспилотных ЛА.

Материалы и методы. Процесс полета уклоняющегося ЛА описывается вектором фазового состояния y ( t ), противодействующего — вектором z ( t ), _где y ∈ Rⁿ , z ∈ R^m .

Динамика взаимного движения описывается нелинейными дифференциальными уравнениями следующего вида:

Машиностроение и машиноведение

^y ( t ) = fy ⁽ У , t ) + g u ^(u , У , z , t), y⁽t 0 ) = У о ,                                          ⁽¹⁾

z ( t ) = f ⁽ z , t ) + g v ⁽ v , z , y , t ), z^(t 0 ) = z 0 ,                                           ⁽²⁾

где f _y, f _z, g_u, g_v — функции своих аргументов, непрерывные и дифференцируемые достаточное число раз; u, v — функции управления соответственно уклоняющимся и противодействующим ЛА, ( u е R , v е R^p ) ;

t g [ t ₀, t k ] — время решения задачи уклонения, t ₀ и t k , соответственно, моменты начала и окончания процесса уклонения [2].

Для решения задачи заданы некоторые компоненты вектора состояния уклоняющегося ЛА в конечный момент t_k i-x

y( tk ) = y, где (i' = 1,n,, n, < n), а yi являются заданными краевыми значениями состояния ЛА, образующими требуемую терминальную область, являющуюся гладким многообразием следующего вида:

уА t k ) - У =^ф yi ( У , t k ) = ⁰, i = 1, П 1 ,                                         ⁽³⁾

где Ф_y — векторная функция размерности n , х 1.

Условиями задачи задается также требование оптимизации (предположим — максимизации) известной скалярной функции остальных n ₂ ( n , + n ₂ = n ) фазовых переменных вектора y ( t k ):

L [ У п , + i ( t k ) , y n +2 ( tk ) ,-, y n + n 2 ( tk ) ; t k ]= L ( y , t k ) .                                       ⁽⁴⁾

В общем случае противодействующий ЛА может быть задействован в любой момент движения уклоняющегося ЛА по траектории, проходящей через терминальную область (3). Этот момент времени t 0 начала реализации игры, а также начальные условия свои и противодействующего ЛА в соответствии с ранее принятым допущением на борту уклоняющегося ЛА определяются мгновенно и точно. Задачей уклоняющегося ЛА в дальнейшем является формирование стратегии уклонения с учетом терминальных ограничений (3), (4). В таком случае общее время реализации игры заранее неизвестно и конечный момент времени t_k не фиксирован. Поэтому и в соответствии с общепринятым подходом будем считать t k параметром ( t_k <  t k , t_k — максимальное время решения задачи, определяемое физическими возможностями игроков, запасами энергии и др.), который должен быть выбран в дополнение к управляющей функции уклоняющегося ЛА u ( t ) так, чтобы минимизировать время игры [3].

Процесс взаимного движения уклоняющегося и противодействующего ЛА заключается в следующем.

Целью управляемого движения уклоняющегося ЛА с момента t 0 является максимизация расстояния от противодействующего ЛА в момент t_k , а противодействующего ЛА, наоборот, минимизация этого расстояния.

Соответственно управляющие функции ЛА u ( t ) и v ( t ) в процессе взаимного полета уклонения-противодействия должны обеспечивать максимум для уклоняющегося и минимум для противодействующего заданной неотрицательной скалярной функции L₂ ( y,z,t ) , характеризующей расстояние между ЛА.

Рациональным является подход, учитывающий ограниченность времени процесса уклонения-противодействия, за счет естественной ограниченности на борту взаимодействующих ЛА энергетических ресурсов, расходуемых на реализацию формируемых управлений, заданных интенсивностями управлений, соответственно:

t_{k r}                                       t_{k p}

I u = JZ kiu? ( t ) ^d t ^и I v = JZ k jvA ( t ) ^d t .

1 0 i =1                                     1 0 j =1

Тогда задачу нахождения допустимых оптимальных стратегий управления u⁰ ( t ) и v⁰ ( t ) необходимо решать

в условиях максимина:

J ( u ⁰, v ⁰ ) = max min uv

^tk_rL            1

- J ( u, v ) = Li ( y, tk )+Jj L2 ( y, z, t) + -( v (t) Kiv ( t )-u tn ^                  2

tk

( t ) K 2 u ( t ) ) ^ d t ^ ,           (5)

t ₀

где K 1, K2— симметричные положительно определенные матрицы соответствующих размерностей [4].

Рассмотрение такой задачи в классической постановке математического аппарата дифференциальных игр является затруднительным ввиду особенностей реализации взаимного движения.

Значительный объем публикаций, посвященных решению игровых задач в классической постановке, предопределяет существенные трудности учета всех известных концепций [2, 5, 6]. В общем случае подходы, использующие альтернативное локальное условие существования седловой точки, требуют при их реализации значительных вычислительных затрат при решении задачи (1)–(5), что обусловлено сложностью интегрирования системы уравнений в частных производных Айзекса и необходимостью достижения условий (3), (4). Поэтому необходимо учитывать обстоятельство, что в сформулированной частной задаче требуется получить решение с точки зрения интересов только лишь одного игрока — уклоняющегося ЛА [7]. В этом случае является целесообразным использование одного из частных подходов, который обеспечивает возможность построения эффективного в вычислительном отношении бортового алгоритма реализации оптимальной стратегии управления уклоняющимся ЛА. Алгоритм базируется на сведении исходной игровой задачи уклонения-перехвата к задаче одностороннего управления уклоняющимся ЛА и исключении требования по выполнению условия существования седловой точки.

На основании этого подхода решение задачи поиска оптимальной стратегии управления для уклоняющегося ЛА u ⁰( t ) будет уже осуществляться не из условия (5), а из более узкого условия следующего вида:

J [ u °; v ( z , y , t ) ] = max { J [ u , v ( z , y , t ) ] } .                                      (6)

При этом управляющая функция противодействующего ЛА v ( z , y , t ) в задаче (1)-(4) с учетом (6) формируется на собственных наблюдениях за движением уклоняющегося ЛА для его перехвата. Также при решении задачи необходимо учитывать, что противодействующее ЛА имеет возможность воспользоваться любым неоптимальным поведением уклоняющегося ЛА и его замкнутое управление формируется «наилучшим» образом по принципу обратной связи без запаздывания [7].

Подход к решению подобной задачи, но без учета терминальных ограничений вида (3) рассмотрен в работе [8]. Здесь решение основано на поиске субоптимального управления движением ЛА, описываемым квазилинейными дифференциальными уравнениями в частных производных, а его недостатком является сложность технической реализации ЦВМ беспилотного ЛА.

В данной работе приводится эффективная в вычислительном отношении методика, в которой для формирования субоптимальной стратегии уклоняющегося игрока используется преобразование двухточечной краевой задачи (ДТКЗ) к одноточечной задаче интегрирования системы обыкновенных дифференциальных уравнений на основе метода инвариантного погружения (МИП) [8].

Однако применение МИП затруднительно для случаев, когда время решения задачи t_k . не фиксировано и целевой функционал содержит неквадратичную терминальную составляющую [7]. Поэтому на данном шаге вместо МИП используется метод решения краевой задачи, рассмотренный в работе [9].

Тогда получается следующее решение задачи формирования субоптимальной стратегии управления уклоняющегося ЛА u 0 ( t )в конфликтной задаче о преследовании с терминальными ограничениями и незаданным временем реализации игры (1)–(4), (6).

Для динамической системы в игровой задаче уклонения-перехвата

Машиностроение и машиноведение

^x ( t ) = f ( x , t ) + g ( x , u , v , t ) , x ( t 0 ) = X o , X o =| y 0    z 01 ” ,                                 ⁽⁷⁾

совокупность необходимых условий экстремума функционала (6), определяющих оптимальную стратегию управления уклоняющегося игрока u0 (t) при условии, что противодействующий ЛА формирует позиционное управление с обратной связью v (x, t) имеет вид [2, 8]: , где x =|y z”, x e R"+m, f =|fy  fl” , g =|gu gv”,

H ( x , u , v , X , t ) = - L 2 ( x , t ) - 0.5 v ^T ( x , t ) K 1 v ( x , t ) + 0.5 u ^T ( t ) K ₂ u ( t ) +

+X ” (t) f ( x, t ) + X ” (t) g ( x, u, v, t), v (x, t ) = K1-1 0

a g v ( ^x , v , t ) d v

X ( t ) ,

- min { H [ x ( t ) , u ( t ) , v ( x , t ) , X ( t ) , t ] } = - min { 0.5u ^T ( t ) K ₂ u ( t ) + X ( t ) g ( x , u , v , t ) } = H ( x , X , t ) , при этом сформированная субоптимальная траектория x ( t ) и вектор сопряженных переменных X ( t ) описываются следующими уравнениями ДТКЗ:

x ( t ) = f ( x , t ) - G v ( x , X , 1 ) ” X ( t ) — 2

-G. (x, X, t) £     11 т  5H (x, X, t) = v ox        ^ Hj       dX

^f x ⁽ x , ^X , t ) , x ⁽ t 0 )    x 0 ,

G v ( x , X , t ) = ° ^g< x ^,X , t ) K

o g ( x , X , t ) o v

X ( t J^ 1 _№0 1 X ( t ) + 1 Px ( t ) т r ^{d G} ^( x ₁ £ ) ®x( t ) )! + ^{o H (} x , ^x , t ) = f x ( x , X , t ) , o x            o .x            2        ^    d x          J         o x

^X i ( t k ) = ^<

Y i , i = 1, n i , ^o L i ( x , t k ) — .      ^o x

i = n + 1, n 1 + n ₂, x = x ( t_k ) ,

Y = - M y^{- 1} Y ,

tk

M Y = J л ^т ( t )

t 0

a g u ( x , u , t ) d u

8g, (x , u , t )!     _{z x}            t k      , _xdg, (x , u , t ) f _{z x}             , _x og, (x , u , t )!

u(,, , )   Л(t)dt,7 = |лт (t)   u( , , )luт (t)K2 +Xт (t)   u ( , , ) [ dt, ou                    ,            ou

-I                            t0                                      IJ

u = u ⁰ ( t ) ,

Л(,)= j№M 1" +rog(x;u;1) 1" 1A(,) , л( tk ) = | I 0 r, OX

л где 0 — введенная в [7] операция блочного произведения блочных матриц; y — постоянный вектор n1 х 1

множителей Лагранжа для терминальной (геометрической) связи (3); Л , М_y , y — матрицы n х n 1 , n 1 х n 1 и

вектор n 1 х 1 соответственно; I — единичная матрица размерности n 1 х n 1 .

Время окончания игры t k находится при этом из дополнительного скалярного уравнения

^{0 L1 (} x ’ t^k ) + H ( x , u ⁰, v , X , t_k ) = 0, o tk        ^{v          k}

где j = j ( t k ) для j = x , u °, v , X .

Существование обратной матрицы Мy 1 определяется условием управляемости преследуемого объекта

и, кроме того, m конечных условий для X ( t_k ) не определены [10].

Для простоты рассуждений можно воспользоваться упрощенным способом преобразования краевой задачи к одноточечной задаче интегрирования системы обыкновенных дифференциальных уравнений, при интегрировании которой вместо оптимальной траектории x ( t ) получают приближение x ( t ) [11].

Обозначим

Q ( ^x , t k ) = Y

⁰ L i ⁽ x , t_k )

0 x i

x = ^x ( t k ) .

Тогда вместо соотношений (8)-(10) получим:

x ( t ) = M 1 ( x , Q , t )

х

0 Q ( x , t )

0 x

M 1 ( x , Q , t ) - M 2 ( x , Q , t )

-1

х

0 Q ( x , t )     ,          _x ,          xll /          x

--- ---- ^fx ( x , ^Q , t ) ^{+ f} x ( ^x , ^Q , t ) k ^fx ( x , ^Q , t ) , 0 x

0 f_x ( x , Q , t ) _z .   Of ( x , Q , t ) _{z x}

M1 (x, Q, t) = Jx (,v' ) M1 (x, Q, t)+ Jx (’^ ) M2 (x, Q, t), ox                          o^^

0 f ( x , Q , t ) _{z x}   of ( x , Q , t ) _{z x}

M2 (x, Q, t) = 2x1^2M1 (x, Q, t)+ A(      )M2 (x, Q, t), ox                    ox

где Q = Q ( x , t ) , x = x ( t ) .

d x ( x_n ( t ), t )     ,       дХ ( Х_п ( t ), t )

Для матриц чувствительности M₁ =---0---- и M₂ =----0---- заданы начальные условия следую-

• ¹        дХ ₀           ²        дХ ₀

щего вида:

M₁ = 0; M ₂ = E,                                           (15)

где E — единичная матрица размерности ( n + m ) х ( n + m ) .

Результатом интегрирования системы дифференциальных уравнений (12-15) является субоптимальная программная траектория уклоняющегося ЛА x(t ) = | y ( t ) ^T z(t ) ^T | , которая обеспечивает его уклонение от противодействующего ЛА и доставку полезной нагрузки в требуемую конечную область (3).

Синтезируемая субоптимальная траектория x ( t ) адаптируется к текущим условиям функционирования уклоняющегося ЛА по результатам идентификации его динамических характеристик.

Траектория получена на основе представления о наиболее вероятных действиях противодействующего ЛА для перехвата уклоняющегося ЛА и с учетом ограниченности энергетики уклоняющегося ЛА в задаче приземления в заданную область (3). Однако стратегия поведения, основанная на однократно определенной программной траектории, не обладает свойством адаптации и приводит к большим методическим ошибкам [12, 13].

Исходя из того, что решение двухточечной краевой задачи получено приближенным методом и модель движения обоих игроков не всегда адекватна функционированию реальных ЛА, необходимо увеличивать частоту обновления навигационных измерений (уменьшить такт решения навигационной задачи). Это в конечном счете приведет к получению близкого к оптимальному (субоптимальному) решения задачи оптимального управления в форме синтеза. При этом устойчивость решения задачи может быть обеспечена рациональным выбором такта для контура наведения ЛА.

Использование алгоритмов с прогнозированием для ЛА различного назначения показало их высокую эффективность вследствие присущего им свойства адаптации к текущим условиям полета и изменяющимся характеристикам ЛА [14, 15, 16].

Применение для маневрирующих беспилотных ЛА оптимального терминального управления для разработки адаптивных алгоритмов с прогнозом обеспечивает высокое качество их функционирования в условиях действия возмущений большой интенсивности при наличии жестких ограничений на параметры траектории и управление [7].

По этой причине окончательный выбор решения сформулированной задачи может быть сделан в пользу использования методологии синтеза алгоритма с прогнозирующими моделями [14].

Методика формирования управления уклоняющимся ЛА в форме синтеза основывается на следующем [17].

С использованием текущих навигационных измерений определяются начальные условия x(t 0 ) = x 0 ( j = 0,  1,  2,... — номер итерации в блоке), и в длиннопериодическом («медленном») контуре решения задачи

Машиностроение и машиноведение

наведения прогнозируется субоптимальная траектория xj (t) на последующий интервал движения уклоняющегося ЛА t е[10, T] (t° = 10, 10 > 10). В короткопериодическом («быстром») контуре решается задача стабилизации движения ЛА относительно субоптимальной траектории x (t) на интервале времени до пересчета управле- ния в контуре наведения.

В течение одной итерации построения программной оптимальной траектории в «медленном » контуре наведения по текущей навигационной информации y (10) в «быстром» контуре стабилизации выполняется не сколько итераций [18]. При этом задача навигации решается с тактом, меньшим или равным такту «быстрого» контура [19]. Соответственно, такт решения задачи в «быстром» контуре определяется динамическими характеристиками уклоняющегося ЛА для обеспечения требований устойчивости, управляемости и др., а такт длиннопериодического контура ограничен вычислительными характеристиками бортовой ЦВМ. Такое кусочнопрограммное управление на интервале времени медленного контура при уменьшении такта будет стремиться к замкнутому управлению в форме синтеза [2].

Результаты исследования. С целью проверки работоспособности, реализуемости и оценки характеристик вычислительной эффективности представленного подхода было выполнено численное моделирование . В качестве уклоняющегося ЛА использовалась модель гипотетического беспилотного летательного аппарата, технические характеристики которого заданы в соответствии с приведенными в работе [20].

Так как полная модель такого типа ЛА обладает чрезмерной сложностью и трудоемкостью, то приняты упрощающие допущения о линейной аппроксимации коэффициентов аэродинамических сил и моментов. В этом случае размерность модели равна 12, она линейна относительно вектора управления и в векторной форме имеет вид (1). С целью упрощения численных исследований рассматривался участок полета в плоскости движения без маневрирования по углу атаки в течение временного интервала T=100 с. Поэтому углы разворота рулей высоты и направления задавались постоянными и равными 0, а управление формировалось только за счет изменения силы тяги ЛА, действующей вдоль его продольной оси.

Модель противодействующего ЛА задана ракетной осесимметричной схемой, а его движение определялось в той же системе координат и в той же плоскости движения и описывалось четырьмя известными детерминированными дифференциальными уравнениями, которые в векторной форме имели вид (2) [15, с. 79]. При этом «неизвестное» уклоняющемуся ЛА управление противодействующего ЛА синтезировалось оптимально по принципу Беллмана — путем минимизации функции промаха [21, 22]

^Q [ У ( tk ) , z ( tk ) ] = ^0,5 ( ^k 1 ( У 1 - z 1 ) 2 + k 2 ( У 2 - z 2 ) 2 )

t = t k

где y i , z i — компоненты фазовых векторов объектов (их координаты в плоскости стрельбы); k i — масштабирующие коэффициенты ( i=1,2).

При этом использовалось предположение, не влияющее на общность полученных результатов, что противодействующему ЛА «мгновенно» известна текущая информации о взаимном расположении обоих ЛА и его управление синтезируется без временной задержки [2, 8, 15].

Для моделирования было выбрано два практических случая управления уклоняющимся ЛА. В первом случае формировалось программное релейное управление с одним переключением на 30-й секунде полета с режима полета с уровнем средней тяги на форсированный режим с уровнем максимальной тяги. Моделирование показало, что ЛА перехватывал уклоняющийся ЛА на 61-й секунде, т.е. задача уклонения с положительным исходом не решалась.

При моделировании второго случая процесса уклонения синтезировалось управление уклоняющимся ЛА на основе сформированной методики из условия максимизации функции промаха (16). При учете энергетических возможностей обоих ЛА и использовании сформированного исходного критерия вида (5) оптимальная функция управления тягой двигательной установки уклоняющегося ЛА Р_ЛА (t) имела релейный вид с двумя переключениями с минимального значения уровня тяги P min на максимальный уровень P max .

Моделирование подтвердило эффективность такой стратегии управления. Задача уклонения решалась с положительным исходом.

Таким образом, моделирование подтвердило, что формирование управления с возможностью переключения тяги двигательной установки с кратностью два и более обеспечивает большую техническую возможность уклонения и адаптации к характеристикам противодействующего ЛА.

При моделировании размерность системы дифференциальных уравнений, интегрируемой в прямом времени, была равна 380.

Требуемое быстродействие бортовой ЦВМ системы управления составило величину не более 1.4*10 5 Коп/сек, для числа операций контура наведения —около 7*10 4 Коп с тактом 0,5 сек. Это подтверждает возможность реализации алгоритма управления в реальном масштабе времени на современных ЦВМ [15, 19].

Применение для формирования управления традиционного минимаксного подхода на основе решения уравнений в частных производных приводит к алгоритму, включающему реализацию дополнительных специализированных численных методов, существенно увеличивающих вычислительные затраты, и в рассмотренном случае высоких размерностей динамических объектов (12 и 4 соответственно) практически нереализуемо на борту в реальном масштабе времени [23].

Результаты моделирования приведены на рис. 1-3.

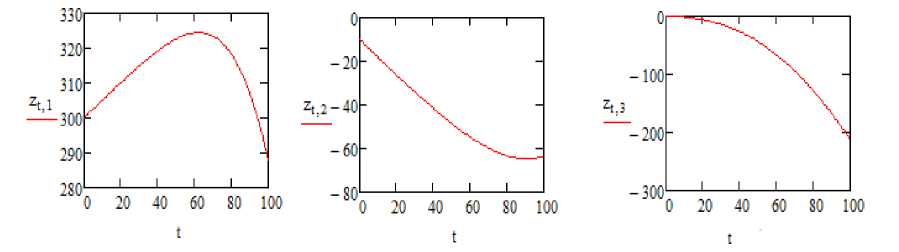
Рис. 1. График линейных скоростей беспилотного ЛА по осям x,y,z (м/с)

Fig. 1. Graph of linear velocities of unmanned aerial vehicle (UAV) along x,y,z axes (m/s)

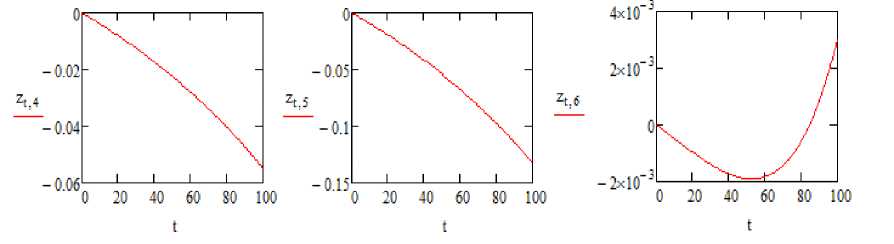
Рис. 2. График угловых скоростей беспилотного ЛА по осям x,y,z (рад/с)

Fig. 2. Graph of angular velocities of UAV along x,y,z axes (rad/s)

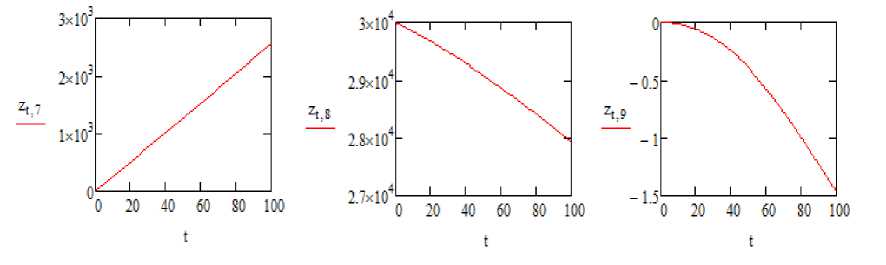
Рис. 3. График координат движения беспилотного ЛА по осям x,y,z (м)

Fig. 3. Graph of movement coordinates of UAV along x,y,z axes (m)

Результаты моделирования процесса уклонения ЛА демонстрируют работоспособность алгоритма и возможность его реализации на современных бортовых ЭВМ в реальном времени.

Обсуждение и заключения. Несмотря на то, что формирование субоптимальной стратегии наведения уклоняющегося ЛА в заданную терминальную область осуществляется не в форме прямого синтеза, многошаговый пересчет программного управления позволяет адаптироваться к текущим условиям. Это достигается за счет многошаговой итерационной процедуры регулярного пересчета терминальных условий, что эквивалентно периодическому замыканию обратной связи. Таким образом, выведение уклоняющегося ЛА в заданную терминальную область осуществляется программно, а управление уклонением от противодействующего ЛА эквивалентно формированию управления в форме синтеза. Ограничениями на применение метода являются условия, что модель движения противодействующего ЛА известна и он формирует естественное управление с целью перехвата уклоняющегося ЛА.

Машиностроение и машиноведение