Синтез закона регулирования привода глубинного штангового насоса в автоматическом режиме

Привод глубинного штангового насоса при работе в автоматическом режиме, как правило, для цели управления использует только одну варьируемую величину – количество двойных ходов механизма в минуту n . Если определен критерий управления, то дальнейшей задачей является синтез закона регулирования, оптимизирующего этот критерий.

Синтез закона регулирования

В качестве критерия нефтедобычи автором используется величина [1]

G = q — k 1 ■ ( n + a- n 2 ) - к 2 ■ n ,                                                                        (1)

где q – оценка величины текущей производительности насоса (иногда эту величину называют текущим дебитом скважины);

M = k 1 ■ ( n + a ■ n 2 ) - расходы на электроэнергию в единицу времени;

D = к 2 ■ n - расходы на обслуживание глубинного оборудования и привода штангового насоса в пересчете на единицу времени.

Постоянные величины к 1 , к 2 , a можно получить на основе экспертных оценок. Они могут меняться в зависимости от цены на нефть (цены добычи нефти), цены на электроэнергию, цены и стоимости обслуживания глубинного оборудования и насосной установки.

Критерий (1) имеет одну точку максимума в рабочем диапазоне количества двойных ходов, характеристика его монотонна, поэтому можно записать квадратичный критерий

G 1 = — [ q — k 1 ■ ( n + a ■ n ) — к 2 ■ n ] ,                                                                       (2)

который имеет минимум в той же точке, что и максимум критерия (1).

В качестве пригодных для использования в станциях управления насосной установкой алгоритмов управления годятся только адаптивные алгоритмы, то есть такие, параметры которых в ходе управления меняются, так как меняются во времени и параметры скважины и самой насосной установки. К таким методам управления можно отнести метод синтеза функций Ляпунова, обеспечивающих устойчивость системы с коррекцией [2]; подход, при котором в ходе управления определяются параметры линеаризованной модели установки, и на каждом шаге алгоритмов синтезируется управление, исходя из оптимизации целевой функции (прогнозирующее управление [3], управление с идентификацией [4] и пр.) и подобные.

Для оценки значения количества двойных ходов в минуту используем прогнозирующее управление разомкнутого типа. В данном случае будущие прогнозирующие управления на всем горизонте прогноза зависят только от текущего состояния системы, т. е. не используется будущая обратная связь.

Зависимость производительности установки q от количества двойных ходов n , исходя из физических особенностей системы, можно описать линейным уравнением

q ( к + 1) = q ( к ) + A ( к ) ■ [ n ( к + 1) — n ( к )].                                                              (3)

Прогнозирующие управления определяются по следующему правилу: на каждом шаге k минимизируем критерий со скользящим горизонтом управления

m

J ( k + m I k ) = - § [ q ( k + i ) - ( k 1 + k 2 ) • n ( k + i ) - k 1 - a- k ( k + i ) • n ( k + i )]² ,                         (4)

i = 1

полученный из (2), где m – горизонт прогноза, по последовательности программных управлений n ( k | k ), …, n ( k + p – 1| k ), зависящих только от состояния системы в момент k . В качестве управления в момент k берем n ( k ) = n ( k | k ). Тем самым получаем управление n ( k ) как функцию состояния q ( k ), т. е. управление с обратной связью. Чтобы получить управление n ( k + 1) в следующий момент, процедура повторяется для момента k + 1.

На управление (количество двойных ходов) накладывается ограничение nmin(k) ^ n(k) ^ nmax(k)•                                                                             (5)

Выражаем последовательно все q ( k + i ) ( i = 1,2, …, m ) через q ( k ) с использованием (3) и подставим в (4). Имеем mi

J(k + m I k) = -§[q(k) + § A(k + j - 1) • [n(k + j) - n(k + j - 1)] - i=1            j=1

• - ( k 1 + k ₂) • n ( k + i ) - k 1 -a- n ( k + i ) • n ( k + i )]² = § [ q ( k ) + § A ( k + j - 1) • [ n ( k + j ) - n ( k + j - 1)] -

• i=1            j=1

  -(k1 + k₂) • n(k + i) - k1 •a • n(k + i) • n(k + i)]²- [q(k) + § A(k + j -1) • [n(k + j) - n(k + j -1)] -j=1

  -(k1 + k₂) • n (k + m) - k1 •a • n (k + m) • n (k + m )]².

Рассмотрим производную от (6):

d J ( k + m I k )     _ _r ... m . .. _{r n} ..           . ...

——----— = -2 •[q(к) + § A(к + j - 1) •[n(к + j) - n(к + j -1)] - dn (k + m)               j=1

- ( k 1 + k ₂) • n ( k + m ) - k 1 •a^ n ( k + m ) • n ( k + m )] • [ A ( k + m - 1) - ( k 1 + k ₂) - 2 • k 1 •a^ n ( k + m )] =

• - 2 • [ q ( k ) + § 1 A ( k + j - 1) • [ n ( k + j ) - n ( k + j - 1)] - A ( k + m - 1) • n ( k + m - 1) + j = 1

+ ( A ( k + m - 1) - k 1 - k 2 ) • n ( k + m ) - k 1 • a • n ( k + m ) • n ( k + m )] x

x [ A ( k + m - 1) - ( k 1 + k ₂) - 2 • k 1 • a • n ( k + m )].

• (7)    можно переписать в виде

6J(k + mIk) = -2 • [p + q • n(k + m) + R • n(k + m) • n(k + m)] • [5 + T • n(k + m)] = dn (k + m)

= -2•[P • 5 + (P • T + Q• 5) • n(k + m) + (T• Q + R • 5) • n(k + m) • n(k + m) +

+R • T • n(k + m) • n(k + m) • n(k + m)], где

P = q ( k ) + § A(k + j - 1) • [ n ( k + j ) - n ( k + j - 1)] - A ( k + m - 1) • n ( k + m - 1); j '= 1

Q = A ( k + m - 1) - k 1 - k ₂;

R = - k1 • a;

5 = A ( k + m - 1) - k 1 - k ₂;

T = - 2 • k 1 •a .

Общей задачей является минимизация (6) по значению управления n(k + m). Эта точка соответствует нулевому значению производной (8). Решая это уравнение, можно получить искомое значение управления n(k + m). Прямое определение управления по этой методике может привести к неустойчивому решению (у автора при просчете управление менялось по ограничениям), так как реальная система описывается сложным нелинейным уравнением, а уравнение типа (3) достаточно точно описывает ее только вблизи одной точки. Поэтому в данном случае целесообразно вести управление по закону n (k + m) = n (k + m -1) ±An,                                                             (10)

так как в этом случае мы на каждом шаге будем ограничивать шаг изменения искомого количества двойных ходов привода.

Задачу можно свести к выбору знака изменения количества ходов и его величине. При этом на каждом шаге управления согласно второго метода Ляпунова необходимо, чтобы dJ (k + m I k)

An ~-------—.(11)

d n ( k + m )

Отсюда из (8) следует

A n ~ P • S + ( P • T + Q • S) • n ( k + m ) + (T • Q + R • S ) • n ( k + m ) • n ( k + m ) +

+R • T • n(k + m) • n(k + m) • n(k + m).(12)

Если коэффициент а из (2) равен нулю, то в этом случае коэффициенты R и T из (12) равны нулю, и можно записать

An ~ P • S + Q • S • n (k + m),(13)

• т. е. A n будет иметь тот же знак, что и величина ( P • S + Q • S • n ( k + m )).

Поскольку в момент вычисления A n величина n ( k + m ) у нас неизвестна, то в качестве нее можно принять величину количества двойных ходов в предыдущий момент времени, тогда получим

A n ~ P • S + Q • S • n ( k + m - 1).                                                              (14)

Аналогично для общего случая ( а ^ 0) можно записать

A n ~ P • S + ( P • T + Q • S) • n ( k + m - 1) + ( T • Q + R • S ) • n ( k + m - 1) • n ( k + m - 1) +

+ R • T • n ( k + m - 1) • n ( k + m - 1) • n ( k + m - 1).                                                   (15)

Можно сформулировать общий алгоритм управления для случая, например, горизонта прогноза, равного трем.

• 1.    При текущем количестве ходов вычисляется производительность насоса и n (3) принимается равным ему, а q (3) – текущему значению производительности, задаемся значением начального приращения количества двойных ходов A _нач, задаем значение текущего приращения количества двойных ходов A n = A _нач .

• 2.    Устанавливается количество ходов, равное текущему минус 2 • A _нач. После окончания переходных процессов получаем значение текущей производительности и n (1) принимается равным текущему количеству двойных ходов, а q (1) – текущему значению производительности.

• 3.    Устанавливается количество ходов, равное текущему плюс A _нач. После окончания переходных процессов получаем значение текущей производительности и n (2) принимается равным текущему количеству двойных ходов, а q (2) – текущему значению производительности.

• 4.    По трем точкам ( n (1), q (1)), ( n (2), q (2)), ( n (3), q (3)) вычисляем A (3) и принимаем A (1) = A (2) = A (3).

• 5.    Смотрим в (14) (или (15)) знак изменения значения количества двойных ходов. Если знак поменялся относительно предыдущего хода, то принимаем A n = A n /2 (используем метод деления пополам). Если A n < A n min , то заканчиваем алгоритм, в противном случае меняем значение двойных ходов согласно (10), где знак изменения определяется (14) (или (15)). При вычислениях учитываем ограничения на количество двойных ходов согласно (5).

• 6.    После окончания переходных процессов получаем значение текущей производительности. Производим сдвижку запомненных значений производительности, количества двойных ходов и коэффициентов n (1) = n (2), n (2) = n (3), q (1) = q (2), q (2) = q (3), A (1) = A (2), A (2) = A (3). n (3) принимается равным текущему количеству двойных ходов, а q (3) – текущему значению производительности. По трем точкам ( n (1), q (1)), ( n (2), q (2)), ( n (3), q (3)) вычисляем A (3).

• 7.    Идем к п. 5.

При вычислении A (3) по трем точкам ( n (1), q (1)), ( n (2), q (2)), ( n (3), q (3)) можно использовать любой метод линейной аппроксимации, например, метод наименьших квадратов [5].

Для горизонта прогноза, равного двум, алгоритм будет иметь вид:

• 1.    При текущем количестве ходов вычисляется производительность и n (2) принимается равным ему, а q (2) – текущему значению производительности, задаемся значением начального приращения количества двойных ходов А _нач, задаем значение текущего приращения количества двойных ходов А n = А _нач .

• 2.    Устанавливается количество ходов, равное текущему минус А _нач . После окончания переходных процессов получаем значение текущей производительности и n (1) принимается равным текущему количеству двойных ходов, а q (1) – текущему значению производительности.

• 3.    По двум точкам ( n (1), q (1)), ( n (2), q (2)) вычисляем A (2) = ( q (2) – q (1))/( n (2) – n (1)) и принимаем A (1) = A (2).

• 4.    Смотрим в (14) (или (15)) знак изменения значения количества двойных ходов. Если знак поменялся относительно предыдущего хода, то принимаем А n = А n /2 (используем метод деления пополам). Если А n < А n min , то заканчиваем алгоритм, в противном случае меняем значение двойных ходов согласно (10), где знак изменения определяется (14) (или (15)). При вычислениях учитываем ограничения на количество двойных ходов согласно (5).

• 5.    После окончания переходных процессов получаем значение текущей производительности. Производим сдвижку запомненных значений производительности, количества двойных ходов и коэффициентов n (1) = n (2), q (1) = q (2), A (1) = A (2). n (2) принимается равным текущему количеству двойных ходов, а q (2) – текущему значению производительности. По двум точкам ( n (1), q (1)), ( n (2), q (2)) вычисляем A (2).

• 6.    Идем к п. 4.

Результаты моделирования при ограничениях количества двойных ходов n min = 1 и n max = 6,5, начальным значением шага А n = 1 и точностью алгоритма до 0,06 хода в минуту для горизонта прогноза, равного трем и двум соответственно (рис. 1 и 2). Значения коэффициентов из (2) показаны там же.

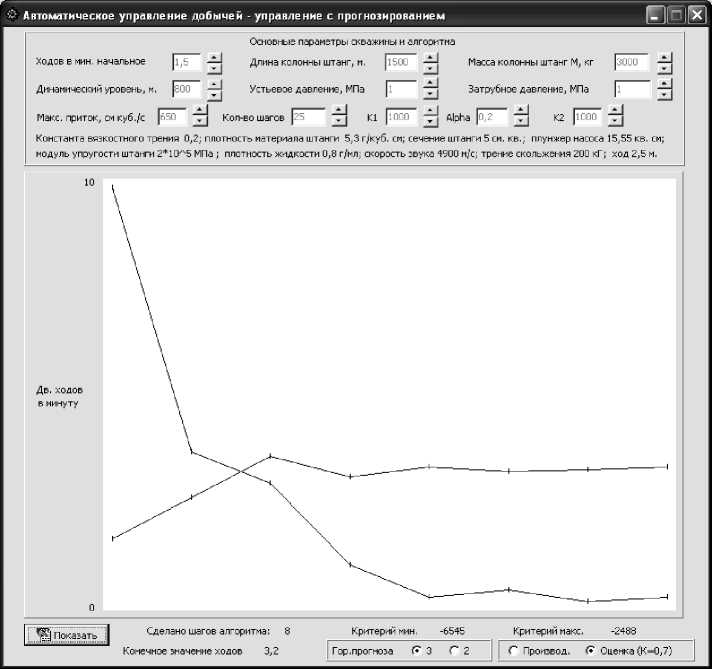
Рис. 1. Изменение критерия вида (2) и количества двойных ходов. Горизонт прогноза равен трем

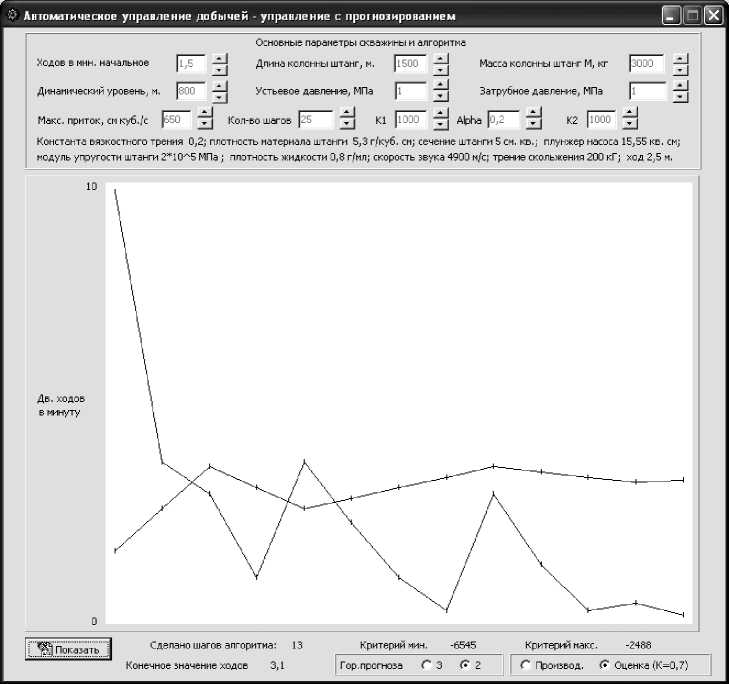
Рис. 2. Изменение критерия вида (2) и количества двойных ходов. Горизонт прогноза равен двум

Из рис. 1 и 2 четко видны прогнозирующие свойства алгоритмов (критерий двигается в одном направлении, а значение управляющей величины – количества двойных ходов – меняет направление движения). При вычислениях производительности насоса в программе бралась его оценка, полученная из обработки данных динамограмм, а само моделирование производилось по методу, аналогичному приведенному в [6].

Можно вести управление, определяя необходимое количество двойных шагов путем прямой максимизации критерия (1). При этом шаг изменения количества двойных ходов будет переменным. Алгоритм будет выглядеть следующим образом:

• 1.    При текущем количестве двойных ходов вычисляется значение производительности q c . Знак изменения количества двойных ходов Sign принимается равным 1. Задаемся начальным значением изменения числа двойных ходов A n .

• 2.    Устанавливается количество ходов, равное n = n + Sign • A n .

• 3.    При текущем количестве двойных ходов вычисляется значение производительности q _н.

• 4.    Если q н >  q c , то принимаем q c = q н и идем к п. 2.

• 5.    Если q н <  q c , то принимаем q c = q н , меняем шаг изменения количества двойных ходов A n = A n / 2 , принимаем Sign = -Sign.

• 6.    Если A n <  A n min , то заканчиваем алгоритм, в противном случае идем к п. 2.

Этот алгоритм реализует метод оптимизации путем деления интервала пополам [7].

Результаты моделирования процесса управления приведены на рис. 3.

В целях корректного сравнения данных при моделировании использовались те же данные, что и для прогнозирующего управления.

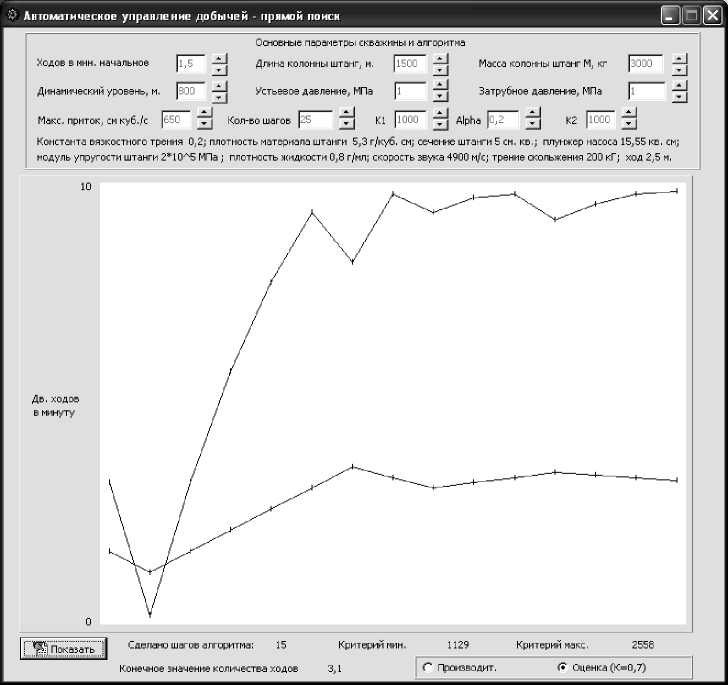
Рис. 3. Изменение критерия вида (1) и количества двойных ходов при прямом поиске

Выводы

В качестве пригодных для реализации законов регулирования приводов глубинного штангового насоса в автоматическом режиме можно использовать адаптивные методы регулирования. Путем цифрового моделирования показана эффективность применения для данной цели прогнозирующего управления, где в качестве модели зависимости производительности установки от количества двойных ходов используется линейная модель, а изменение количества двойных ходов происходит с переменным во времени шагом.