Синтезированные на приёмном конце канала связи голограммы 3D-объекта в технологии Dot Matrix

Вопросы создания голографического TV всё больше обсуждаются специалистами как в области голографии, так и в области кодирования изображений. Объединённая группа экспертов по фотографии (Joint Photographic Experts Group–JPEG) даже объявила конкурс предложений для решений по голографическому кодированию [1, 2]. При этом с самого начала комитет JPEG Pleno, который занимается голографическим кодированием, наряду с задачами пленоптики, где каждый кадр мультиплицируется матрицей линз с несколькими градациями их фокусных расстояний, в своём стандарте (ISO/IEC 21794 [3]) предполагает решения для кодирования более полных данных светового поля [4] в виде создания массива 4D-данных о световой волне с последующим чисто математическим устранением избыточности, вроде кодов Хаффмана, и повышения таким образом энтропии кодированного сообщения. Однако при этом там же говорится о слишком больших требова- ниях как к объёмам обрабатываемой таким образом информации, так и к скорости их обработки, поскольку каждый кадр, представляющий собой 3D-массив данных объекта регистрирования, должен меняться во времени с принятой в основных TV-стандартах частотой смены кадров. Такой подход реализуется сегодня в рамках технологий облака точек [5, 6], полигонального [7, 8] и воксельного [9, 10] представления объёмных изображений. О его неэффективности в применении к задачам 3D TV и 3D-дополненной реальности говорит уже то, что при большой активности разработчиков в последние 2–3 десятилетия эти технологии не смогли пробиться дальше компьютерных игр, представляя движущиеся фигурки, существенно отличающиеся от изображений живых людей. Действительно, передача динамически меняющейся во времени 3D голографической информации требует не только большой производительности компьютеров, но и огромной пропускной способности канала её передачи [11, 12]. Настолько большой, что одна голографическая трансляция прямого гологра- фического контента с принятым разрешением и частотой кадров, аналогичными Full HD, займёт весь доступный радио- и телевизионный диапазон, вытеснив все другие радио- и телепередачи. Другой подход был представлен в [13, 14] и защищён в патенте РФ [15]. Его суть сводится к тому, что для создания 3D-голографического изображения на приёмном конце канала связи не обязательно передавать всю голографическую информацию. Достаточно передать только часть, отвечающую за модуляцию несущей. И хотя модуляция в голографии имеет более сложный вид, но это очень похоже на метод SSB, поскольку пространственные частоты несущей вводятся уже на приёмном конце канала связи. В [13] было предложено передавать вместо всей голографической информации только часть, соответствующую одной боковой полосе частот, но в виде двух 2D-изображений, к каждому из которых уже применено JPEG-сжатие. Первое из этих двух изображений – это текстура поверхности 3D-объекта, подобная обычной фотографии или их серии в видео. Второе – это карта 3D-поверхности, на которую текстура накладывается, образуя изображение 3D-объекта, или маска объекта. Такой метод регистрации информации о 3D-объекте в одном кадре текстуры не фиксирует информации об объектах, находящихся «в тени» более близких к съёмочной камере, однако этот же вопрос поставлен и в других работах, например по упомянутым выше Pleno технологиям, и выходит за рамки настоящей работы.

Таким образом, было предложено решить проблему передачи голографической информации по обычному каналу связи. Другими словами, можно сжимать 3D-голографическую информацию до двух 2D-кадров стандартного разрешения, что не представит трудностей при её передаче практически без потерь, поскольку каждый из этих двух кадров может быть сжат известными алгоритмами. При реализации такого метода возникает ряд вопросов и проблем, анализу которых и прямому экспериментальному доказательству возможности его реализации посвящена настоящая работа. Здесь мы приводим экспериментальные результаты синтеза такой голограммы на приёмном конце канала связи.

1.    Постановка задачи

Для решения задач голографического TV и 3D-дополненной реальности ранее было предложено [16] выделять часть пространственных частот голограммы, соответствующих девиации несущей пространственной частоты. Она возникает за счёт сложения с опорным пучком объектного пучка сложной формы, который несёт информацию как о поверхности регистрируемого объекта, так и о её яркостной структуре. Последний тоже может быть сложной формы, и тогда необходимо выделять девиацию частот на фоне сложного пространственного спектра. Такая поста- новка задачи в передаче радиосигналов в доступной литературе не известна. Однако в голографии она встречается не редко и решается сравнительно легко [17]. Как показано в [16], именно девиация пространственных частот на голограмме несёт информацию о фазе и амплитуде регистрируемого объекта. Сама несущая (или комбинация частот, как бывает при кодированном опорном пучке) выполняет другую роль – пространственное разделение дифрагировавших на голографической решётке минус первого порядка, несущего информацию об объекте, и нулевого, проходящего через голограмму в направлении восстанавливающего пучка. Таким образом, несущая и её девиация имеют разную физическую природу, и их можно независимо друг от друга изменять, что само по себе позволяет прямо на приёмном конце канала связи перемещать восстанавливаемое 3D-изображение из одного участка электромагнитного спектра в другой. Кроме того, при сравнении несущей и её девиации выясняется, что они могут отличаться в миллионы раз [13, 16]. Модуляция этой пространственной несущей меняющимся в пространстве объектным пучком вызывает её девиацию. Величина последней не нужна большей, чем диапазон пространственных частот TV- кадра высокой чёткости. Такие изменения в кадре просто не видны. А голограмма воспроизводит оптический сигнал с микроскопическим разрешением в тысячу раз бо́ льшим телевизионного разрешения. Поскольку как TV-кадр, так и голограмма являются двумерными, то для прямой передачи голографического сигнала того же размера, что и TV-кадр, возникает проблема, связанная с передачей уже не в тысячу раз большей информации, а в миллион. Как было описано в [13], предложенный в патенте [15] способ сжатия голографической информации устраняет эту проблему.

В [18] приведены результаты прямых опытов по передаче по обычному радиоканалу сжатой таким образом голографической информации. Такая передача 3D-голографической информации по своей сути похожа на известную в радиотехнике передачу информации на одной боковой полосе (SSB), когда несущая частота отвечает за дифракцию восстанавливаемого голограммой 3D-изображения объекта в нужный порядок, а модуляция регистрируемым объектом предметного пучка – за девиацию пространственных частот. Поскольку экспериментально была доказана возможность прямой передачи двух 2D-изображений нужного качества с требуемой частотой смены кадра, последним этапом на пути демонстрации практической возможности передачи 3D-голографической информации является восстановление материальной голограммы по принятой на приёмном конце канала связи 3D-информации, переданной на одной боковой полосе. Другими словами, необходимо показать практическую возможность внесения в переданную на SSB 3D-информацию несущей пространственной частоты (или комбинации пространственных частот), необходимых для синтеза полноценной голограммы. Один из вариантов синтеза голограммы Э. Лейта и Ю. Упатниекса и восстановления ей 3D-изображения сложного регистрируемого объекта – портрета человека был нами показан в численном виде [13]. Другой – в [19] в виде материального объекта – радужной голограммы С. Бентона, в технологии проекционной системы Dot Matrix. В этой технологии запись голограммы осуществляется последовательной проекцией на носитель фрагментов компьютерной стереограммы, рассчитанной по набору плоских ракурсных фотографий 3D-объекта [20]. Хотя такая голограмма и создаёт эффект горизонтального параллакса при повороте голограммы вокруг вертикальной оси, но в каждый момент времени наблюдатель видит одну из плоских картин – одну из проекций 3D-объекта. Это хорошо работает, создавая иллюзию 3D в маленьких (Ø~20 мм) защитных голограммах, но очень бросается в глаза в голограммах размером уже больше 4÷5 см, не говоря уже о портретах в натуральную величину. И хотя на приёмный конец канала связи нами была передана информация, достаточная для синтеза голограммы, восстанавливающей полноценное 3D-изображение, необходимость уже на приёмном конце канала сначала превращать её в набор плоских картинок, хотя и с любым количеством изопроекций, мешает восприятию полноценного 3D-объёма.

2.    Запись голограмм и объективные измерения их структуры

Для более убедительного доказательства работоспособности предложенного в патенте [15] метода в настоящей работе приводятся результаты эксперимента по синтезу материальной голограммы уже не с набора плоских изопроекций 3D-объекта, а c использованием его 3D-маски (рис. 1).

На рис. 1: а ) приведена текстура одного кадра поверхности живого, изменяющегося во времени объекта c разрешающей способностью 2000 × 2000 пикселей в кадре, т. е. превышающей стандарт Full HD. Здесь она приведена в серых тонах, хотя можно передавать и цветное изображение, например в стандарте RGB; б ) карта глубин поверхности регистрируемого 3D-объекта, имитирующая его глубину в 256 слоёв, т. е. соответствующая стандарту Full HD; в ) 3D-маска, созданная по карте поверхности. На рис. 2 приведены восстановленные голограммами 3D-изображения. Голограммы рассчитывались по маске рис. 1 в методом, заявленным в [20, 21].

б)

в)

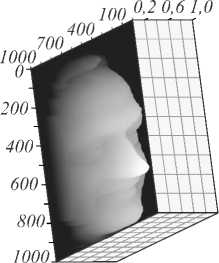
Рис. 1. Регистрируемый 3D-объект: а) текстура поверхности; б) карта глубин поверхности; в) 3D-маска

б)

а)

Рис. 2. Восстановленное голограммами изображение: а) голограммой, изготовленной в технологии Dot Matrix

с регулярным расположением голопикселей со скважностью 1,5; б) голограммой в технологии Dot Matrix с нерегулярным расположением голопикселей в форме многоугольников, покрывающих всю 3D-поверхность маски

Расчёт структуры голограмм в отличие от прямого преобразования Френеля и его интерференции с опорным пучком, в отличие от расчёта радужной голограммы С. Бентона в [19] в технологии проекцион- ной системы Dot Matrix с многоракурсными фотографиями 3D-объекта, проводился с учётом угла наклона локальных участков 3D-маски (рис. 1в). В голограмме рис. 2а сначала находились нормали к поверхности маски рис. 1в, расположенные в узлах прямоугольной сетки, а затем по (1, 2) вычислялся период решётки голопикселя. В голограмме рис. 2б, исходя из структуры поверхности маски, определялись участки примерно одинакового наклона в виде многоугольников (полигоны) и по их наклону также с помощью (1, 2) вычислялся период решетки для каждого полигона. В первом случае легче вводить изменение яркости, пропорциональное текстуре рис. 1а, а во втором можно получать бо́ льшую дифракционную эффективность [20, 21].

В обоих случаях решалось уравнение дифракции Брэгга в 3D-пространстве (1), в котором по заданным волновым векторам восстанавливающей опорной волны kr и восстановленной объектной ko для каждого участка s поверхности 3D-объекта (маски) находился вектор решётки KS, который затем проецировался на плоскость голограммы.

K s = k o - k r .                                        (1)

Или по аналогии с дифракцией на кристаллах решалась система линейных уравнений Лауэ [22], в которых направление дифракционных максимумов удовлетворяет одновременно условиям (2):

J d x (cos ф x - cos § x ) = M X [ d y (cos ф y - cos ^ y ) = N X

Здесь, d x , d y – проекции на соответствующие оси периодов синтезируемой голографической решётки; φ x , φ y – углы, образуемые падающим, а ξ x , ξ y – рассеянным излучением; λ – длина волны восстанавливающего излучения; M , N – целые числа. Таким образом, в рамках геометрической оптики решается обратная задача, когда по набору ξ x , ξ y и φ x , φ y для М = N = 1 находились d x , d y , определяющие локальные значения периода d голографической решётки и её азимута для каждого локального участка s голограммы, на которые она была предварительно разбита полигональной системой голопикселей.

В случае, когда s большое настолько, что можно пренебречь дифракционными эффектами, такая голограмма представляет собой киноформ со сложной структурой. Согласно условию дистанции Рэлея (3), это выполняется, когда s >> λ L s (или m >> 1), где L S – глубина объекта на s- (м) участке его поверхности.

J<< 1 ^ дифракция Фраунгофера s I m =---<1 + 10 ^ дифракция Френеля . (3) X Lz

[>> 1 ^ геометрическая оптика

В этом случае дифракция на таком участке не важна и все расчёты по (1) соответствуют требованиям геометрической оптики. Этот случай соответствует киноформной оптике, иногда называемой литоголограммой. Видно, что такой киноформ хорошо ра- ботает при сравнительно небольших глубинах объекта. С ростом LS, когда s ~ λ LS или s < λ LS, дифракционным рассеянием уже нельзя пренебречь и голограмма больше соответствует эшелетту [20]. Для более полного соответствия технологии эшелеттов, обеспечивающей более яркое восстановленное изображение, необходимо выдерживать условие равенства наклона профиля полос и периода решётки таким образом, чтобы отражённый от наклонного участка полосы свет распространялся в ту же сторону, как и минус первый порядок дифракции на этой решётке [21]. Однако выдерживать такие соотношения для сложной голографической структуры полос невозможно, поскольку выдерживая их для одного наклона голограммы, мы тем самым нарушаем их для другого. Поэтому такие голограммы будут восстанавливать 3D-изображения яркими, но существующими в небольшом угловом пространстве.

Для записи голограммы, приведенной на рис. 2 а , была использована проекционная система «DotMatrix». Соответствующая голограмма (её фрагмент на рис. 3 а ) экспонируется небольшими участками – фреймами. Изображение системы полос выводится на жидкокристаллический пространственный модулятор, освещаемый лазером через формирователь пучка, и с уменьшением проецируется на регистрирующую среду. После экспозиции одного фрейма столик перемещается на его величину и снова записывается очередной участок системы полос. В зависимости от яркости изображения в каждой точке меняется площадь заполнения голопикселя решёткой. Таким образом достигается модуляция яркости на голограмме согласно яркости соответствующих участков текстуры регистрируемого объекта. В процессе записи фреймы с разрешением 1920 × 1080 точек поочередно выводятся на ЖК-модулятор и проецируются микрообъективом на фоточувствительную пластину с уменьшением до 0,3 × 0,169 мм. Для синтеза голограммы потребовалось около 10⁶ пикселей на 1 погонный миллиметр её поверхности.

а)

б)

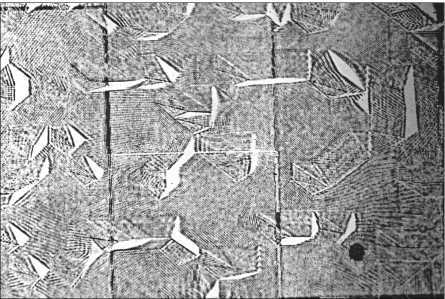
Рис. 3. Микрофотография структуры голограммы: а) восстанавливающей 3D-изображение рис. 2а б) восстанавливающей 3D-изображение рис. 2б

Голограмма рис. 3б рассчитывается аналогично, но покрытие решётками поверхности фоторезиста осуществляется непрерывно, как проекция полигонов, покрывающих 3D-поверхность регистрируемого объекта. В этой технологии повышается общая площадь дифракции и вместе с ней дифракционная эффективность синтезированной голограммы, но отсутствует прямая возможность изменять площадь полигонов, как в предыдущей технологии, что мешает изменять яркость участков голограммы пропорционально яркости используемой текстуры объекта.

На рис. 3 а приведена микрофотография структуры голограммы, восстанавливающей 3D-изображение рис. 2 а . Размер голопикселя в виде квадрата с дифракционной решёткой внутри составляет 9,5 мкм. Период решётки в пикселях представленного сегмента по микрофотографии голограммы можно оценить как варьирующийся между 0,5 и 1 мкм. Стрелкой показано место сопряжения двух записываемых участков голограммы, производимое механическим перемещением столика. Для видимого диапазона длин волн (λ ~0,5 мкм) m < 1 для всех глубин объекта Lz > 0,17 мм, т. е. действительно, структура голограммы рис. 3 а , согласно критерию Рэлея, представляет собой голограмму, а не литоструктуру.

Другой способ записи заимствовал разбиение 3D-поверхности на треугольники из полигональной графики [7, 8], когда поверхность 3D-объекта покрывается множеством треугольников с общими гранями. В оригинале три точки каждого треугольника и задают поверхность 3D-объекта. Каждый такой треугольник можно спроецировать на поверхность голограммы и создать на его поверхности дифракционную решётку тоже по (1, 2). Эшелетт при таких маленьких периодах решётки создавать трудно, хотя начальные шаги в этом направлении уже ведутся [23, 24, 25]. Подготовка технологии записи голографических решёток, приведённых на рис. 3 б , осуществлялась также в рамках работ [20, 21].

Такая голограмма приведена на рис. 3б. На основе карты глубины создаётся объёмный объект из плоского, затем идет операция сглаживания пиксельной структуры, затем специальной текстурой создаётся матовая поверхность, а в конце этот объект совмещается с текстурой объекта. Видно, что получаемая голографическая структура имеет дифракционный рельеф, однако также видны и пустоты, свободные от голографических решёток. Вероятно, это связано с тем, что некоторые сформированные пространственные частоты были слишком большими и не смогли быть перенесены записывающей системой на фоторезист. Сравнение по формуле (3) реализованных размеров полигонов {s ~ (17)2 мкм}, несущих в себе различные дифракционные решётки, также показывает, что при записи голограмм с глубиной регистрируемого объекта LZ > 0,55 мм условия дифракции вступают в силу на большой части голограммы, а при LZ > 1 мм уже на всей её площади. Таким образом, представленные на рис. 3а, б синтезированные дифракционные структуры являются полноценными голограммами. Можно считать, что таким образом в сигнал, сформированный переданными по каналу связи картой поверхности (маской) и текстурой, была рассчитана и внесена несущая частота, на которой дифрагирует восстанавливающий пучок, формируя изображение записанного 3D-кадра.

Структура микрорельефа голограммы на рис. 3 б , её полигоны имеют более сложную форму, и для её объективного анализа нужно привлекать специальные системы, разработанные в ИАЭ СО РАН для анализа структуры рельефно-фазовых голограмм [26, 27].

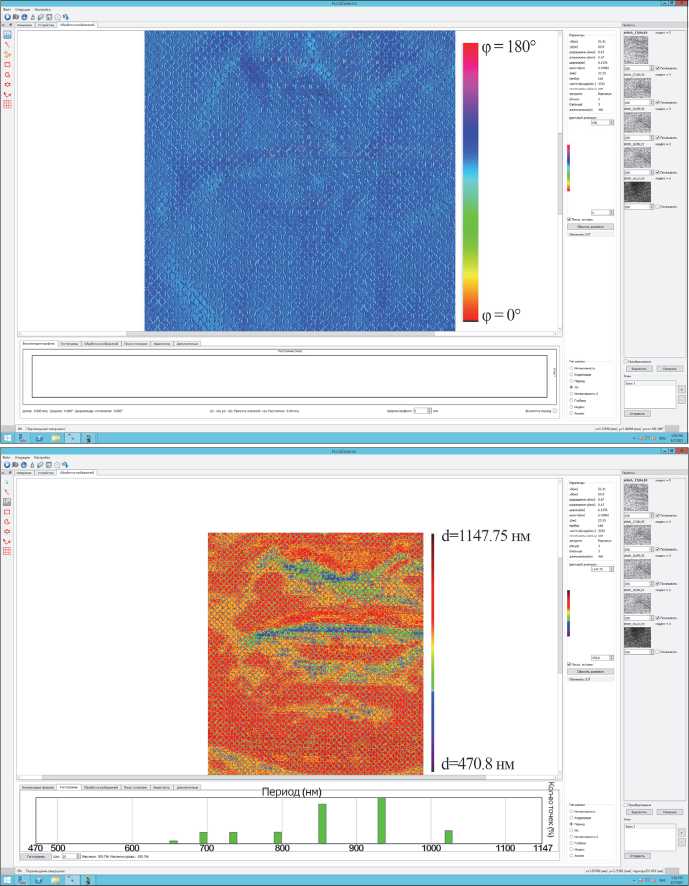
С их использованием можно примерно оценить (рис. 4 а , б ) размеры треугольных полигонов, сечения которых сравнением со шкалой рис. 4 а можно определить как 10–20 мкм, средний период дифракционных решёток, заполняющих полигоны, – от 0,47 мкм до 1,15 мкм.

Структура решёток голопикселей, как видно из рис. 3 и рис. 4, состоит из прямых линий. Каждый голопиксель представляет собой полигон размером от 17 до 34 мкм с решётками периодом от 0,47 до 1,15 мкм со средним периодом 0,9 мкм. Средний азимут направления решёток составляет 60° с девиацией ± 10°. Несколько облегчает задачу синтеза такой голограммы то, что и девиация периода, и девиация азимутальных изменений решёток по её полю незначительны. Последнее связано с большим, около 45°, наклоном опорного пучка.

Из структуры голограммы, представленной на рис. 3 а , б , и измеренных характеристик (рис. 4 а , б ) видно, что синтезированная голограмма обладает несущей частотой и её девиацией, что представлено как изменяющимся периодом, так и азимутом решёток. Значит, мы получили на приёмном конце канала связи [16, 18] полноценную голограмму. Видно (2), что d x , d y определяют несущую частоту голографической дифракционной решётки при постоянных ξ x , ξ y и φ x , φ y и λ, а при изменении ξ x , ξ y и φ x , φ y , вызванном модуляцией опорного пучка объектным, наблюдается девиация d x , d y . Также видно, что несущая пространственная частота сравнительно легко может быть изменена уже на приёмном конце канала связи изменением значения λ. Это удобно для мультиплексирования 3D-изображений, поскольку маска остаётся постоянной для любой текстуры, будь то видимое, ИК- или УФ-изображение. Так же легко реализуется расчёт голограммы с переносом 3D-изображения из одного участка электромагнитного спектра в другой. Даже можно использовать смешанные источники формирования 3D-сигнала, например, формировать текстуру электромагнитным излучением, включая радиодиапазон, а маску – используя акустическое зондирование. Такой синтез голограмм на приёмном конце канала связи позволяет сравнительно легко синтезировать голограммы гиперспектральных изображений и может быть применён для задач 3D TV и дополненной реальности.

а)

d=l 147.75 нм d=470.8 нм

<р= 180°

<р = 0°

■__1

И т w ип

Рис. 4. Статистика структуры решёток голограмм: а) по периоду; б) по азимуту

Экспериментальные измерения характеристик восстановленных такими голограммами 3D-изображений приведены ниже.

3.    Измерения характеристик восстановленных голограммами изображений

У обеих голограмм (рис. 3а, б) была измерена глубина восстановленного ими 3D-изображения. Для этого использовалась [16] бителецентрическая телескопическая система рис. 5. В область проекции 3D-изображения этой телескопической системы помещались два маркера в виде игл. Путём их перемещения настраивались положения, когда при поперечном смещении наблюдателя концы маркеров не смещались относительно точек изображения. Таким образом добивались одинакового параллакса восстановленного изображения и прямого изображения этих маркеров. Последующее измерение продольного вдоль оптической оси расстояния между концами этих игл и определяло глубину восстановленного изображения. Корректируя это расстояние с учётом продольного увеличения телескопической системы, рассчитывалось продольное расстояние между двумя точками объекта, восстановленного голограммой. Выбирая максимально удалённую точку и максимально приближенную, определяли глубину восстановленного голограммой объекта.

На рис. 5 приведены: а ) оптическая схема бителецентрической телескопической системы, позволяющая выносить в пространство измерений 3D-изображение, восстановленное голограммой и б ) фотография реально используемого телескопического устройства с добавленными в неё проекциями 3D-изображений.

Объективы O1 и O2 образуют бителецентрическую телескопическую систему. С помощью голограммы восстанавливается изображение 3D-объекта на входе в телескопическую систему. Измерения параллакса проводятся регистрацией совмещённых с передним и задним планами 3D-изображений мерительных маркеров камерой, перемещающейся поперёк оптической оси на L’p.

На рис. 6 приведены две фотографии восстановленного 3D-изображения с мерительными маркерами, позволяющими определить глубину каждого изображения.

Результаты измерений сведены в табл. 1.

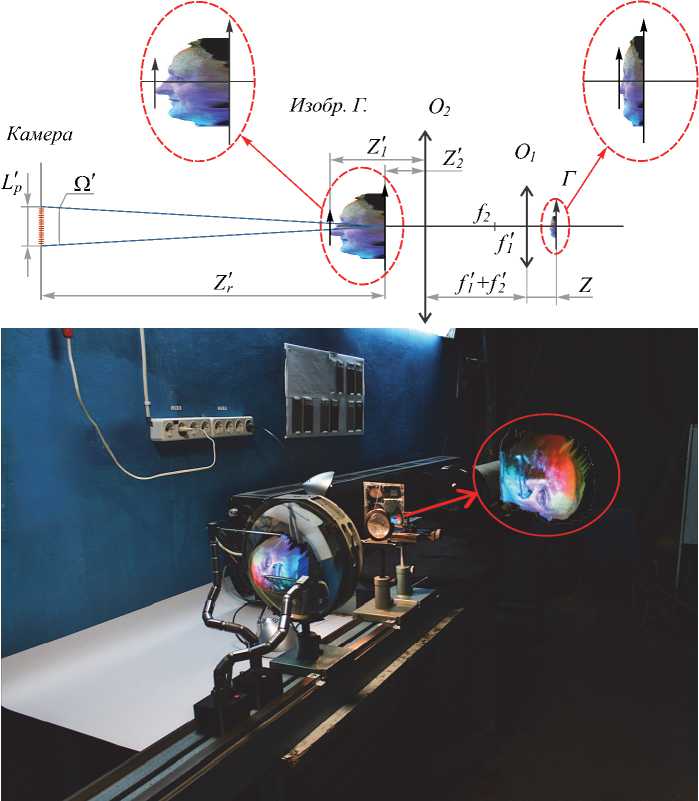
Рис. 5. а) Бителецентрическая телескопическая система O 1 и O 2 ; голограмма Г; изображние восстановленного объекта (ближний план Z’ 1, дальний план Z’ 2 ); угол измеряемого параллакса Ω’; б) фотография экспериментальной телескопической системы (восстановленное голограммой 3D-изображение объекта и оно же увеличенное телескопической системой

вмонтированы)

б)

Рис. 6. Восстановленные изображения с мерительными маркерами в виде игл (нижний маркер ближе, верхний – дальше): а) для голограммы рис. 3а, восстанавливающей 3D-изображение рис. 2а; б) для голограммы рис. 3б, восстанавливающей 3D-изображение рис. 2б

Табл. 1. Результаты измерений параллакса восстановленных изображений рис. 3а и рис. 3б

Голограмма	Рис. 3 а			Рис. 3 б
Восстановленное изображение	Рис. 2 а	1		Рис. 2 б
Поперечный размер объекта на голограмме (мм)	Высота – 20 Ширина – 14			Высота – 20 Ширина – 16
Кратность поперечного увеличения телескопа (крат)	3,1			3,1
Поперечный размер действительного изображения объекта, увеличенного телескопом (мм)	Высота – 20 × 3,1 = 62 Ширина – 14 × 3,1 =43,4			Высота – 20 × 3,1 =62 Ширина – 16×3,1=49,6
Продольный размер действительного изображения объекта, увеличенного телескопом (мм)	14 (измерено экспериментально)			32 (измерено экспериментально)
Пересчитанный продольный размер объекта, восстановленного голограммой (мм)	1,35 (вычислено в ZEMAX)			3,36 (вычислено в ZEMAX)
Параллакс действительного изображения, увеличенного телескопической системой (угловых градусов) измеренный	Ω =2,75°			Ω = 1,47°
Параллакс действительного изображения, восстановленного голограммой (угловых градусов) без телескопической системы вычисленный	Ω’ = 10,5°			Ω’ = 9,27°

Хотя параллакс полученных 3D-голографических изображений и не велик, но мы уверенно наблюдаем в этих голограммах требуемый для нормального восприятия объём.

Так, для голограммы рис. 3 а , восстанавливающей изображение рис. 2 а , глубина восстановленного изображения составила Δ Рис. 3 а = Z 1 – Z 2 = 1,35 мм при ширине объекта 14 мм, а для голограммы рис. 3 б , восстанавливающей изображение рис. 2 б , Δ Рис. 3 б = Z 1 – Z 2 = 3,36 мм соответственно. Это говорит о том, что созданные в рамках настоящего исследования голограммы, несущие один кадр 3D-голографического сигнала, переданного с TV кадровой частотой, вполне удовлетворяют условиям объёмности восстанавливаемых ими изображений, хотя эти голограммы и были созданы численно уже на приёмном конце традиционного канала связи Wi-Fi. При этом скорость передачи, как показано в [18], превышала необходимые 25 пар кадров (текстура + маска) в секунду при качестве кадра, соответствующего качеству Full HD и даже 4K.

Что касается разных отношений глубины к ширине восстановленного изображения на рис. 2 а 1,35 / 14=0,1, а на рис. 2 б 3,36 / 16 = 0,21, то этот вопрос не был принципиальным в решаемой задаче и может быть скорректирован программно, например введением корректирующих коэффициентов в программы расчёта голограмм.

Основные выводы

Результаты настоящей работы показывают возможность практической реализации предложенного в патенте [15] способа передачи 3D-голографической информации, с восстановлением на приёмном конце обычного канала связи 3D-голографического изобра- жения. С учётом работы [18] это является реализацией идеи голографического фототелеграфа. Вместе с решаемыми в настоящее время разными группами разработчиков вопросами быстрого синтеза, отображения и восстановления голограмм в реальном масштабе времени. Полученный в настоящей работе результат является практическим доказательством возможности сравнительно простого варианта передачи и восстановления на приёмном конце канала связи голографического TV-контента и 3D-дополненной реальности. В случае появления голографического монитора эта технология позволит сравнительно просто проводить 3D-сеансы связи без использования специальных шлемов и насадок для глаз.

По сравнению с технологией Pleno такой подход является менее ресурсоёмким и подтверждает возможность реализации настоящих глубоких действительных 3D-динамических изображений с Full HD качеством восстановленного изображения, буквально живущего в пространстве наблюдателя, перед экраном голографического монитора.

В силу разделения несущей частоты и её девиации информационным сигналом метод удобен для мультиплексирования 3D-изображений, их переноса из одного участка электромагнитного спектра в другой, а также при создании гиперспектральных изображений и может быть применён для задач 3D, TV и дополненной реальности.

Такая технология, по мнению авторов, может найти применение не только в развлекательных областях деятельности, но и в телемедицине, в работе с агрессивными средами и в труднодоступных местах, а также в задачах акустической визуализации 3D- объектов, поскольку варианты создания маски поверхности ничем не ограничены и могут создаваться, например, методом эхолокации, а на приёмном конце визуализироваться в видимом диапазоне электромагнитного спектра. Также разделение информации о поверхности 3D-объекта и текстуре его поверхности с информацией о длине волны записи, выражающееся в произвольном изменении несущей пространственной частоты, синтезируемой на приёмном конце канала связи голограммы, облегчает решение задач мультиплексирования и создания 3D-гиперспектральных изображений.