Синусоидальный гауссов оптический вихрь как суперпозиция двух гипергеометрических пучков

Гипергеометрические лазерные пучки, известные в оптике с 2007 года [1, 2], до сих пор привлекают внимание исследователей. Они описываются функцией, которая является точным решением дифференциального уравнения параболического типа (уравнения типа Шредингера), следующего из уравнения Гельмгольца в параксиальном приближении Фока– Леонтовича. Эти пучки представляют собой широкий класс вихревых пучков, которые имеют несколько внутренних параметров и которые содержат как частные случаи модернизированные элегантные пучки Лагерра–Гаусса, Бесселя и другие [3, 4]. Эти пучки можно сформировать с помощью модулятора света или с помощью дифракционных оптических элементов [5, 6]. Были исследованы непараксиальный вариант гипергеометрических пучков [7], их острая фокусировка [8]. Было рассмотрено прохождение таких пучков через среду с гиперболическим показателем преломления [9], через оптическую систему, выполняющую дробное преобразование Фурье [10], через одноосный кристалл [11], среду с параболическим показателем преломления [12, 13], через ABCD-оптическую систему [14] и через оптическую систему с высокой числовой апертурой [15]. Гипергеометрические пучки оказались устойчивыми при распространении в атмосфере с неколмогоровской турбулентностью [16] и при прохождении через океанскую турбулентность [17, 18]. Было исследовано прохождение таких пучков через нелокальную нелинейную среду [19, 20]. В работах [21, 22] исследованы гипергеометрические пучки с резкой автофокусировкой. В [23] исследована дифракция гипергеометрического пучка на решетке с вилочкой, а в [24] рассмотрены силы, которые действуют на рэлеевскую частицу, захваченную в фокус гипергеометрического пучка. В [25] рассмотрен асимметричный гипергеометрический пучок.

В данной работе рассмотрена осевая суперпозиция двух Гауссовых гипергеометрических пучков с разной начальной кривизной волнового фронта, распространяющихся в однородной среде. Показано, что если у каждого пучка в центре начальной плоскости есть особенность и энергия не ограничена, то у суперпозиции особенности нет и энергия ограничена. Подробно исследована такая суперпозиция с единичным топологическим зарядом, которая названа синусоидальным Гауссовым пучком. Радиус основного кольца такого пучка определяется радиусом кривизны волнового фронта и почти не зависит от радиуса перетяжки Гауссова пучка.

1.    Гипергеометрический пучок с начальным параболическим волновым фронтом

Известны гипергеометрические пучки [1], комплексная амплитуда которых в начальной плоскости имеет вид:

• ,x. W      I Г 2

E(r, ф, z = 0) = —exp I---+ in ф|,(1)

• r     I w2

  где ( r , φ , z ) – цилиндрическая система координат, w – радиус перетяжки Гауссова пучка, n – целый топологический заряд пучка (1). У пучка (1) есть особенность в нуле (при r =0), и, несмотря на наличие Гауссова пучка, энергия пучка (1) бесконечная. Но при распространении в однородном пространстве у пучка (1) уже нет особенности. Рассмотрим вместо пучка (1) аналогичный пучок с квадратичной фазой в начальной плоскости. То есть рассмотрим размещение спиральный фазовой пластинки exp(i nφ ) не в перетяжке Гауссова пучка, а в том месте, где пучок сходится (или расходится). Тогда начальное поле вместо (1) будет иметь вид:

  
  

  будет иметь особенность в начале координат и начальное поле будет обладать конечной энергией. Действительно, разность двух полей (2) со знаками плюс и минус равна:

  
  

  _ _ _ I w I x I r ²       'I

  E = E₊ - E_ = — sin br r ²) exp--- + in ф , (7)

  V r ) ^v V w ²        )

  
  

  где b = k /(2 f ). Из (7) видно, что при r =0 амплитуда равна нулю. То есть у поля (7) нет особенности в начале координат, которая была у поля (2). Найдем энергию (мощность) пучка (7) по формуле:

  
  

  / ЛА Г- iw )    К ikr 2    Г ² , ■ I

  E ± ( r , ф , z = 0) = 1 — 1 exp | ±——--- + in ф| ,   (2)

  V 2 r )   ( 2 f   w²      )

  
  

  да                              да

  W = 2 n f E |² rdr = n w ² f

  
  

  sin ² ( bx ) e ^px

  x

  
  

  dx =

  
  

  где k =2π / λ – волновое число света с длиной волны λ, f – фокусное расстояние сферической (параболической) линзы. Распространение поля (2) в однородной среде описывается преобразованием Френеля

  
  

  n w ², । ₁ 4 b ² । n w ², । ₁ z 2 |

  = ^— ln I 1 + ^ I = ^—Г" ln I 1 + XX I , где P = 4 p ² 4 f ²

  
  

  (8) 2/ w ² .

  
  

  Комплексную амплитуду поля (7) на любом расстоянии z можно найти, используя (5). Получим:

  
  

  / -i X да 2n

  E ( p , 9 , z ) = l —— I f f E ( r , ф , z = 0 ) x v ^{2 n} z ) о 0

  
  

  Л A / Л n + 2 V n I z о I I ik p²        I

  E ( p , 9 , z ) = ( - i ) --- — exp ---- + in 9 x

  ^{V 7} 2 V z ) V 2 z         J

  
  
  
  

  x exp — ( r ² + p ² ) - — r p cos ( ф-9 ) rdrd ф , 2 z           z

  
  
  
  

  x[ q + ^1/2 ( z ) e ^{x +} I n Z2 < x + ) - q - ^1/2 ( z ) e ^x - I n /2 < x - ) ] .

  
  

  где (ρ, θ) – полярные координаты в плоскости наблюдения. Подставляя поле (2) в (3) и используя справочный интеграл [3]

  
  

  да

  f exp ( - pr ² ) J n ( cr ) dr =

  
  
  
  

  Решение уравнения Гельмгольца (9) (в параксиальном приближении) хотя и замкнутое, но анализировать его затруднительно, так как модифицированные функции Бесселя имеют произвольный порядок и разные по величине комплексные аргументы. Но при n = 1 функции Бесселя в (9) выражаются через элементарную функцию синус. И поэтому при n = 1 анализ поля (7) в зоне дифракции Френеля можно провести более детально.

  
  

  ^,

  
  

  где J n ( x ) и I n /2 ( x ) – функция Бесселя целого порядка и модифицированная функция Бесселя полуцелого порядка, получим:

  
  

  3. Элегантный синусоидальный Гауссов вихрь с единичным топологическим зарядом

  
  

  E ± ( p , 9 , z ) = ( - i ) n ⁺ 2

  
  
  

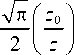
  Г ik P 2    ■ л

  exp-- + in 9

  V 2 z

  
  

  x

  
  
  
  

  Для удобства перепишем еще раз начальное поле (7) при n = 1 и заменим общий множитель w на b ^–1/2 (это размерная константа и не влияет на конечные результаты):

  
  

  x q ± ^1/2 ( z ) exp ( - x ± ) I n /2 ( x ± ),

  
  

  где z 0 = kw ² /2,

  
  

  q ± ( z ) = 1 - iz о ( z ^{- 1} ± f ^{- 1} ) ,

  _r -     ¹ I z I I PI

  x ± = I II I .

  2 q ± ( z ) V z ) V w )

  
  
  
  

  Из (5) видно, что у поля нет особенностей при любом z >0.

  2. Линейная комбинация гипергеометрических пучков

  Далее мы покажем, что линейная комбинация двух начальных комплексных амплитуд (2) уже не

  
  

  E 1 ( r , ф , z = 0 ) =

  
  

  —_ | sin ( br ² ) x r V b )

  
  

  x exp

  
  
  
  

  r ²

  -V + i ф w ²

  
  
  
  

  В зоне дифракции Френеля комплексная амплитуда находится подстановкой (10) в (3) и равна:

  
  

  E ₁ ( p , 9 , z ) = - —sin ( b ( z ) p ² ) x IpV b)   ^v '

  
  

  x exp

  
  

  где

  
  

  _-

  
  

  p ² w ² ( z )

  
  

  ik p ²

  2 R ( z )

  
  
  
  
  

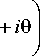
  w ² ( z ) = w ²

  
  

  R ( z ) =

  
  

  4 z o² z ² + ( Y z ² - z 2 ) ² z ° ( z o +Y z ²)

  
  

  4 z 2 z ² + ( y z ² - z 0 ) 2 Y z ( z 0 +y z ²)

  
  

  b ( z ) = bz o²

  
  

  ( Y z ² - z 0 ) + 2 iz o z 4 z ² z ² + ( y z ² - z 0 )²

  
  
  
  

  Y = 1 + b ² w ⁴

  
  

  = 1 + zk .

  f ²

  
  

  Из сравнения (10) и (11) видно, что поле сохраняет свою структуру в зоне дифракции Френеля. Но так как аргумент синуса в (11) комплексный, пучок (11) нельзя назвать модой. Это элегантная мода, то есть мода, у которой сохраняется вид аналитического выражения (11), с помощью которого описывается данная мода. Но распределение интенсивности при распространении изменяется (происходит перераспределение энергии между кольцами картины дифракции, хотя сама картина остается осесимметричной). Известны элегантные пучки Лагерра–Гаусса, амплитуда которых описывается многочленами Лагерра, но с комплексным аргументом [4]. Поэтому интенсивность таких пучков меняется при распространении, хотя и не существенно. Заметим, что зависимость радиуса пучка w ( z ) и радиуса кривизны R ( z ) в (12) отличаются от радиуса перетяжки и радиуса кривизны для Гауссова пучка, так как зависимость от z этих величин в (12) только частичная, другая часть зависимости от z присутствует в аргументе функции sin и «спрятана» в функции b ( z ). Интересной особенностью пучка (10) и (11) является то, что радиус первого (основного) кольца интенсивности почти не зависит от радиуса перетяжки Гауссова пучка w . В начальной плоскости радиус первого кольца можно оценить как половину радиуса, на котором функция синуса в (10) имеет ноль ( br ² = π):

  — max - 7 f /2. (13)

  
  

  Более точное выражение для радиуса первого кольца интенсивности можно найти из условия равенства нулю производной интенсивности поля (10) по аргументу:

  
  
  
  
  
  
  

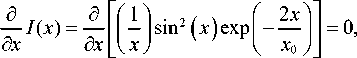
  где x = br ², x 0 = bw ².

  Упрощая (14), получим трансцендентное уравнение для нахождения радиуса первого кольца интенсивности в начальной плоскости:

  
  

  tan x = 2 xx ₀ /2 x + x _o.

  
  
  
  

  Для сравнения напомним, что радиус кольца моды Лагерра–Гаусса (0, 1)

  
  

  E lg 1 ( r , Ф , z = o ) = I ^— I exp I- r - + i ф]            (16)

  I w J I w ²      J

  
  

  зависит от радиуса перетяжки и равен выражению:

  
  

  — max = w /72.

  
  
  
  

  Другой особенностью пучка (11) является то, что он состоит из двух почти Гауссовых пучков с разной расходимостью. Действительно, амплитуду (11) можно представить в виде:

  
  

  E 1 ( p , 9 , z ) = —7= x

  ( 2 p V b J

  (    p ²       ik p ²       )

  x exp I---1---+ i 9 I

  [ w ² ( z ) 2 R ( z ) J x [ exp ( ib 1 ( z ) p ² - b 2 ( z ) p ² ) -- exp ( - ib 1 ( z ) p ² + b 2 ( z ) p ² ) ] ,

  
  
  
  

  где b 1 ( z ) =Re b ( z ), b 2 ( z ) =Im b ( z ). Из (18) получим уравнение для радиуса Гауссова пучка в зависимости от расстояния z для обоих слагаемых:

  
  

  w ² ( z ) = w ²

  
  

  4 z o² z ² + ( Y z ² - z o² ) ² z ² ( z ² +y z ² ± 2 bw ² z _o z )

  
  
  
  

  Знак плюс в (19) относится к первому слагаемому в (18), а минус – ко второму. Можно показать, что наличие минуса в знаменателе формулы (19) не приводит к нулевому и отрицательному значениям знаменателя. Хотя радиусы Гауссовых пучков в (19) разные, в дальней зоне при z >>  z 0 оба радиуса увеличиваются одинаково и линейно от z :

  
  

  w ± ( z >>  z o ) = w g 7Y = w g V1 + z o² / f ² ,

  
  
  
  

  где w G – радиус Гауссова пучка в дальней зоне:

  w_G ( z >>  z _o) = X z / ( n w ).

  Из (20) видно, что расходимость пучка (11) в корень квадратный из «гамма» раз больше, чем расходимость обычного Гауссова пучка. Этого следовало ожидать, так как аргумент синуса в (10) является фазой сферической линзы с фокусным расстоянием f . И эта линза изменяет (всегда увеличивает, так как расположена в перетяжке) расходимость начального Гауссова пучка.

  Однако если сравнивать не с Гауссовым пучком, а с модой Лагерра–Гаусса (0, 1), то расходимость пучка (16) будет равна:

  
  

  w lg 1 ( z >>  z o ) = 72 w g ( z >>  z o ) = 72 —. n w

  
  
  
  

  Это следует из общей формулы для расходимости моды Лагерра–Гаусса ( p, l ) [26]:

  
  

  w LG ( z ) = w^ 2 p + 1 + 1 1 1

  
  
  
  
  

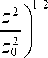
Таким образом, если z 0 <  f , то, как следует из сравнения (20) и (21), расходимость оптического вихря (11) меньше, чем расходимость пучка Лагерра–Гаусса (16).

а)

I, отн.ед.

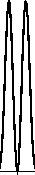
г)

д)

в)

,, I, отн.ед.

0,04

t

i; мм

-5 *

r, MM

-5*

ж)

к)

е)

,, I, отн.ед.

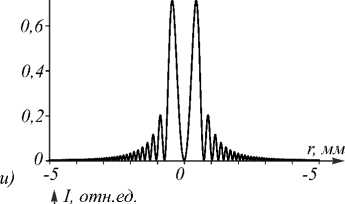
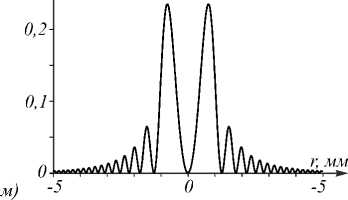
Рис. 1. Распределения интенсивности (левый столбец, негатив), фазы (средний столбец) и сечения интенсивности

(правый столбец) пучка (10) с радиусом перетяжки w 0 = 500 мкм (а – е) и w 0 = 5000 мкм (ж – м) в начальной плоскости z = 0 (а – в, ж – и) и на расстоянии z = 2 м (г-е, к–м).

Остальные параметры расчёта: длина волны λ = 532 нм, фокусное расстояние f = 1 м

4.    Моделирование

На рис. 1 показаны распределения интенсивности и фазы пучка (10) с радиусом перетяжки w 0 =500 мкм и w 0 = 5000 мкм в начальной плоскости z =0 и на расстоянии z = 2 м. Остальные параметры расчёта следующие: длина волны λ = 532 нм, фокусное расстояние f = 1 м.

Из рис. 1 видно, что дифракционная картина состоит из набора световых колец. Согласно распределениям фазы (рис. 1б, д, з, л), в центре картины находится оптический вихрь с единичным топологическим заря- дом. Из распределений фаз также видно, что число световых колец бесконечно и расстояние между ними уменьшается от центра к периферии, что согласуется с формулой (10) (аргумент синуса квадратично зависит от радиальной полярной координаты r).

Из рис. 1 также видно, что, действительно, радиус кольца почти не зависит от радиуса перетяжки Гауссова пучка: при w0 =500 мкм он составил 310 мкм в начальной плоскости и 711 мкм на расстоянии z =2 м, а при w0 = 5000 мкм он в этих плоскостях составил соответственно 442 мкм и 764 мкм. То есть изменение радиуса перетяжки в 10 раз привело к возраста- нию радиуса кольца в начальной плоскости в 1,43 раза, а на расстоянии z = 2 м – всего на 7%. Ещё из рис. 1 видно, что, изменяя радиус перетяжки w0, можно управлять величиной боковых лепестков. Так, если на рис. 1и и 1м интенсивность второго кольца достигает соответственно 28 % и 27 % от интенсивности первого кольца, то на рис. 1в и 1е боковые кольца хотя и имеются, их интенсивность мала и на дифракционных картинах (рис. 1а, в, г, е) их не видно (их наличие подтверждается только распределениями фазы на рис. 1б, д).

Заключение

Рассмотрены гипергеометрические пучки с параболическим волновым фронтом в начальной плоскости, распространяющиеся в однородной среде. Хотя гипергеометрические пучки имеют особенность в центре начальной плоскости и бесконечную энергию, суперпозиция двух таких пучков уже не имеет особенности и имеет конечную энергию. Детально рассмотрен частный случай такой суперпозиции – синусоидальный Гауссов пучок с единичным топологическим зарядом. Этот пучок относится к типу элегантных лазерных пучков, так как и в начальной плоскости, и в зоне дифракции Френеля описывается одной и той же функцией с комплексным аргументом. Диаметр первого светового кольца у синусоидального Гауссова пучка почти не зависит от радиуса перетяжки Гауссова пучка. Изменяя радиус перетяжки у такого пучка, можно управлять величиной боковых лепестков.

Работа выполнена при поддержке Российского научного фонда (грант 18-19-00595, раздел «Элегантный синусоидальный Гауссов вихрь с единичным топологическим зарядом», и грант 22-22-00265, разделы «Гипергеометрический пучок с начальным параболическим волновым фронтом», «Линейная комбинация гипергеометрических пучков»), а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (параграф «Моделирование»).